¹Department of Biotechnology, Koneru Lakshmaiah Education Foundation, Guntur, India

^2,3,4,5,6Department of Petroleum Engineering, KoneruLakshmaiah Education Foundation, Guntur, India

Corresponding author Email: kkchandrika@kluniversity.in

Article Publishing History

Introduction

The generation of biofuels from microalgae is as a result of a high thrill for alternative energy sources. The increasing population which has led to the increase number of vehicles and high energy demand has left the world market with scarcity of fossil fuels (Minneapolis, MN, USA, 2011).  Biodiesel can be obtained from any vegetable oils like sunflower, cotton seeds, peanut, safflower and microalgae lipids, but microalgae has the highest lipid yield (Demirbas and Demirbas, 2013). Algae cultivation is done in open ponds and bioreactors, but to control the growth parameters, algae is cultivated in photobioreactors. Nannochloropsis are algae species of cold-water marine, with high triglycerides (triglyceride is an ester derived from glycerol and three fatty acids) and high growth rate (Archambault, 2014) and therefore, it is most opted as the source of biofuel, (Islam et al., 2013, Mondal et al., 2017 and  Sharma et al., 2019).

Factors affecting microalgae growth include light intensity, PH, presence of nitrogen (Danesi et al., 2002; Colla et al., 2007; Celekli and Yavuzatmaca, 2009), presence of contaminants (Vonshak, 1997), initial biomass concentration (Costa et al., 2002), population density (Vonshak, 1997), temperature, salinity and growth dynamics and much more. All these parameters can be controlled and improved only when the algae cultivation is done in a photobioreactor, instead of an open pond.

It is important to understand growth modelling of organisms and also its behaviour under vast different environmental conditions which include PH, temperature, nutrients (Zwietering et al., 1990; Celekli et al., 2008; Celekli and Yavuzatmaca, 2009) and light intensity.Differentmodels like Gompertz model were used to describe the curve of microbial growth and biovolume production (Zwietering et al., 1990; Celekli et., 2008). These models are also used to predict microbial biomass production and optimizing the growth conditions (Costa et al., 2002; Celekli et al., 2008; Celekli and Yavuzatmaca, 2009). Gompertz model is modified to give lag time, specific rate of growth and stationary phase (maximum population biovolume) (Zwietering et al., 1990; Celekli et al., 2008). Other growth models have been put on the table to describe growth during the cultivation (Rangel-Yagui et al., 2004; Chojnacka and Noworyta, 2004, Mondal et al., 2017  Singh and Singh, 2019).

With the escalating climate change, global warming has been a major concern worldwide. Presence of much greenhouse gas concentrations in the atmosphere is the major cause of ozone layer depletion that leads to global warming, in which carbon dioxide takes a lion’s share with an estimation of 76.7% (v/v) and this concentration has been increasing rampantly from industrial revolution(Sharma et al., 2019). It is estimated that emission of carbon dioxide from coal thermal plants is about 7% (v/v) of global CO₂ emission and that emitted from flue gas of power plants is 10% (v/v) to 15% (v/v), and these exclude the emissions from transportation sector (automobiles)(Natural Gas Production, 2012).

As the population increases, there is an increase in the number of vehicles with high demand of petroleum products which contribute to the emission of greenhouse gases (CO₂ in particular). This has brought the attention to the scientist and researchers to look for ways of mitigating the concentrations of CO₂ from the atmosphere (Sharma et al., 2019).

It’s has been found in some studies that growth of microalgae is much more influenced by carbon dioxide and sunlight; nutrients are also required for biomass production (Mondal et al., 2017). The concern of this paper is to prepare a model that maximizes biomass production from microalgae by use flue gas, for the production of bio-fuel, (Majid et al., 2014).

Flue gas is used to make this model. In flue gas, toxins like SO_x and NO_x have to be put into consideration, the presence of these toxins inhibit algal growth. The use of flue gas as a source of CO₂ for algal growth would reduce the content of emitted CO₂ from automobiles and industries, in the atmosphere. Air contains less percentage (0.04%) of CO₂ and the growth of microalgae that gets CO₂ from the air would be gradual and biomass production minimal. On the other hand, high concentrations of CO₂ would drive microalgae to death phase (Singh and Singh, 2019).

Hence, determining the maximum concentration of CO₂for the growth of algae is more preeminent.

Methodology

Organism and culture conditions for model development

Nannochloropsis limnetica 18.99  was obtained from a culture collection of Algae, SAG, Germany. The culture was grown in a basal medium (Shen and Yuan, 2012) at 30^oC and a pH of 8.0. In all experiments, the initial cell density was maintained at 0.01 g L^-1. Cool white fluorescent lamps were mounted on either side of the glass reactor (bubble column: 30 L; 220 mm dia ; 3:1 H/D) with 100 μmol m^-2s^-1 light intensity. The temperature, pH, and algal growth were monitored every 24 hours. Algal growth was estimated in terms of cell count using a Neubaur chamber (Rohem, India) .The number of cells was converted to equivalent dry weight values by the regression equation.

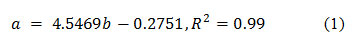
Where α is the dry is weight (g L^-1);  is the cell number expressed in cells L^-1.

Effective growth rate and SO_x inhibitory parameters

A series of experiments were made to determine effective growth rate (µ_eff), consisting CO₂ (% v/v) inputs at different concentrations of SO_x. The PH was adjusted in Erlenmeyer flasks (250mL) with dilute H₂SO₄ (18.4M) to simulate the effect of SO_xin the growth medium, therefore different concentrations of SO₄^2-(0-150 mg L^-1) were generated. The effective growth rate (µ_eff) under a concentration of SO₄^2-(M_SOx) was measured in each experimental flask by recording cell concentration with respect to time.

A linear plot logarithmic cell concentration versus time was then used to derive µ_eff from the slope of the curve. A supplementary linear plot, comprising µ_eff, versusSO₄^2- concentration wasalso used to derive the constant c which is equivalent to specific growth rate ( ) from the Y-intercept and the SO_x inhibitory constant from the slope of the plot following Eq. (10). The critical SO₄^2- concentration (M_t) was also determined from the same plot where the SO₄^2- concentration corresponding to the µ_eff  = 0 was recorded to be the M_t  for the algae.

Growth Model development

The model consists the following factors: (i) The growth inhibition in the presence of flue gas that depends on partial pressures of CO₂ and SO_x;(ii) The substrate (HCO₃^–) concentration is influenced by the pH of the medium; (iii) The effective growth rate (µ_eff) is influenced by critical toxin (M_t) in the medium.

To minimize the complexity, some of the assumptions were made; no external mass transfer influence due to a diffusion process from the head space into the culture, the total pressure of the system is constant at operational gas velocities; the light intensity, temperature and O₂ inhibitory were not considered as but kept constant. The CO₂ in the feed was assumed to be consistent throughout stages of growth and sequestered CO₂ is consistent during the entire exponential phase.

Gas phase CO₂ and SO_x mass transfer and their solubility

The rate of mass transfer of CO₂ and SO_x into the liquid is estimated with an assumption of a steady state and the mass balance of the inlet and outlet volumetric flow rate of flue gas comprising mole fraction of CO₂ and SO_x is as below;

Where  and  are the mass transfer rates of CO₂ and SO_x across air-water interface; G is gas the flow rate,   and  are the inlet mole fraction of CO₂ and SO_x respectively;  and are the outlet mole fraction of CO₂ and SO_x in the flue gas; (mol.w)_CO2 and (mol.w)_Sox are molecular weights of CO₂ and SO₂ respectively; H is the total sparging time of flue gas in a day; Pt is total pressure; and R,T&V are universal constant, absolute temperature and total volume of the liquid respectively.

The concentration of the liquid phase of CO₂ and SO_x in equilibrium with that of CO₂ and SO_x in the flue gas feed is described as follows:

Where    M_Lm is CO₂ concentration at equilibrium; Pt is the total pressure;  is the mole fraction of gas component; He is Henry’s constant for CO₂. Similarly;

Where  is mass transfer of   from gas to liquid medium; R, T and He are universal gas constant, absolute temperature and Henry’s constant of  respectively. Initial substrate (M_L) is an important variable influencing growth rate in the model development, and an assumption of steady state between absorption and consumption of the substrate was made, while CO₂ transfer from the flue gas was driven by M_L gradient in the liquid which is aided by the mass transfer coefficient of the system. Therefore;

Where the volumetric mass is transfer coefficient;  is the equilibrium concentration of CO₂ and  is the concentration of dissolved CO₂ at a defined time. The was estimated experimentally by using the static method. Hence;

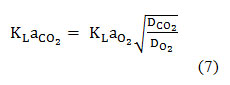
where and  were the diffusivities of CO₂ and O₂ respectively

Inhibitory growth kinetics

To model the effective growth rate appropriately, the effects of CO₂ and SO_x inhibition have to be combined.

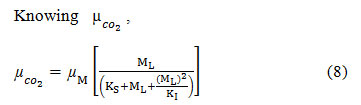
The growth time slows down when SO₄² accumulates during the transfer of SO_xinto the liquid medium, while considering SO_x inhibition along with µCo2  then the growth rate as a function of  is modeled as;

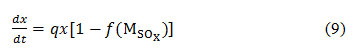
Where  is the dissolved concentration of SO_x in the form of SO₄², q is the SO_x inhibitory constant. When SO_x linearly decreases growth rate,

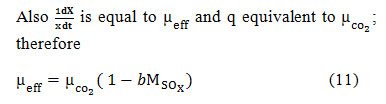
The critical time for SO_x inhibition

The SO_x in the flue gas is toxic to the algal cells when the reduced pH reaches the critical concentration. Thus, it’s of a great significance to correlate the defined mass transfer rate of SO_x in the liquid medium and the time at which the critical concentration is reached.Therefore, toxic time and stationary phase are modelled as follows;

Where is the critical SO_x concentration,  is the dissolved SO_x (SO₄^2-) concentration at a defined time.

Results and Discussion

Toxic components in the flue gas have influence on algal growth, high concentration of CO₂; residual SO_x drastically affect the growth rate.

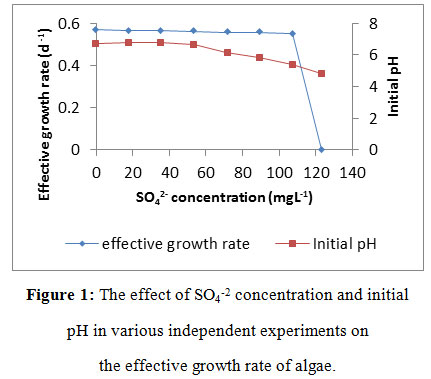Figure 1: The effect of SO4-2 concentration and initial pH in various independent experiments on the effective growth rate of algae.

Figure 1 shows graphical interpretation of effective growth rate against SO_x (SO₄^2-) concentrations with the corresponding values of initial pH. The active growth was under alkaline condition with the pH of 6.8, as SO_x concentration increases, the effective growth rate (µ_eff) decreases linearly with a constant . The effective growth rate fluctuates slightly from 0.48 to 0.43 per day and suddenly to 0.0 at SO_x critical concentration (M_t=123 mgL^-1), and this leads to substrate (HCO₃) depletion and thus affecting the and µ_eff . The change in effective growth rate profile before reaching M_t is insignificant in comparison to µ_eff at M_t. This supports theoretical evidence that  is constant before reaching M_t with less effect of toxin (SO₄²), whereas sudden drop in  at M_t, toxin concentration has a great effect on µ_eff.

Table 1: List of best fit parameter constants and their comparison with literature

Parameter	*Best fit value	Comparable values from literature
µM	0.82 day-1	1.0 day-1;Forján et al. (2007)
KI	1.02 g L-1	10 mM@ ;Silva and Pirt. (1984)
KS	0.07 g L-1	0.12 gL-1;Chen et al. (2010)
Ct	123mg L-1	300 ppm@ (gas phase); Lee et al. (2000)

*The best fit value is the base value in sensitivity analysis; @: K_I and Ct equivalent to 0.44g L^-1and 133mg L¹ (liquid phase concentration) respectively.

Figure 2: Normalized profiles of various predicted parameters (CO2growth rate ( ), substrate concentration (Mt), Biomass concentration (X), effective growth rate ( ), and SOx concentration (MSOx)) in the modelling of algal growth.

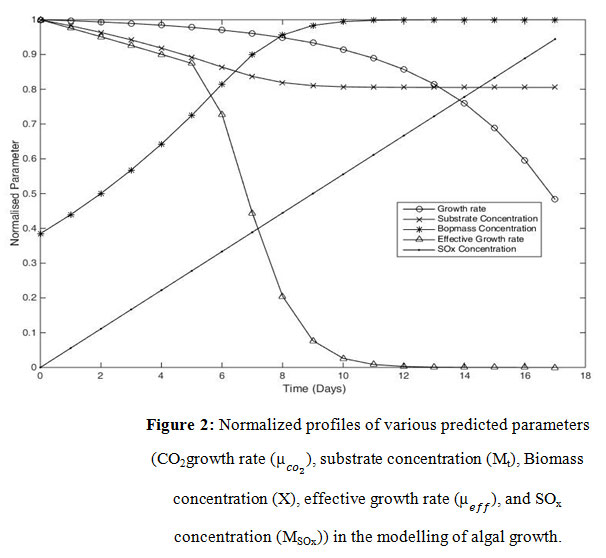
In figure 2, CO₂growth rate ( ), substrate concentration (M_t), Biomass concentration (X), effective growth rate ( ), and SO_x concentration (M_SOx) were taken as normalized parameters against time. Growth kinetics like effective growth rate and CO₂growth rate were plotted with their maximum inputs against time. The  is stable until reaching critical SO_x concentration (M_t) and then declined drastically after reaching, affecting the , according to Eq. (11). Biomass concentration increases with time until it reaches the phase of decline and then remains constant. Substrate (HCO^–₃) concentration depletes as it is consumed during algal growth and becomes constant when the algal growth stops. Since the SO_x concentration is not utilized during the algal growth, it keeps on increasing as flue gas is supplied to the algal culture.

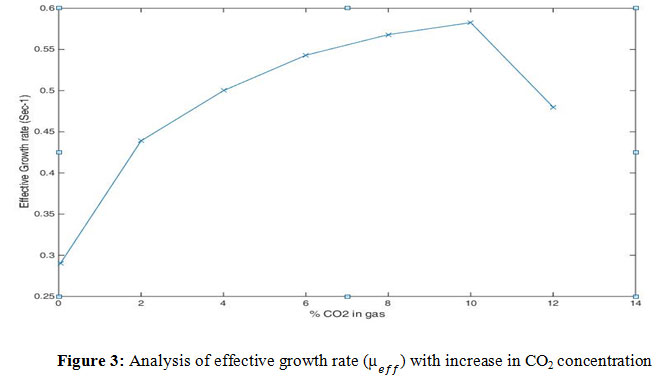Figure 3: Analysis of effective growth rate ( ) with increase in CO2 concentration

Air contains 0.04% of carbon dioxide and the toxins like SO_x and NO_x are negligible and therefore, there is no inhibition of SO_x to the algal growth. The algal  increases as CO₂percentage in the flue gas increases. The increase in the  is seen when carbon dioxide ranges from 0.0004% to 10%. Continuous supplying of CO₂ to the algal culture, beyond 10% of CO2 leads to the decline in the effective growth rate and eventually, to the death phase.

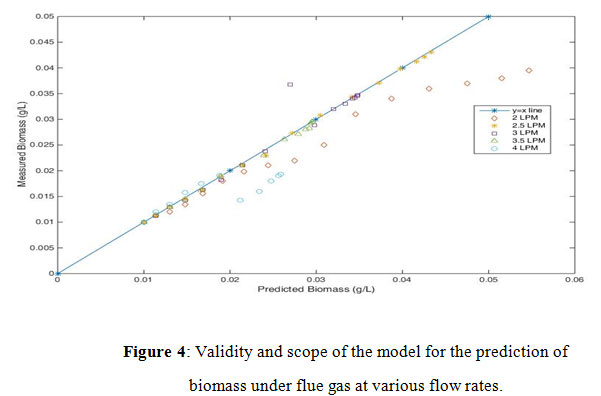Figure 4: Validity and scope of the model for the prediction of biomass under flue gas at various flow rates.

Flow rate is one of the operating parameters and it shows a direct impact on biomass production. Six different flow rates were used to check the validation of the model (Figure 4) by using predicted and experimented biomass concentrations. From the profile shown in figure 4, for the validity of the model for the prediction of biomass, higher deviations are observed at high flow rates of >3.5LPM and at low flow rates of <2.5LPM. The model is valid at the region of flow rates ranging 2.5LPM to 3.5LPM.

Conclusion

In this model, certain amount of carbon dioxide can be reduced from the atmosphere as flue gas from industries or vehicles is used for algal growth. The cell growth was directly affected by SO_x concentration which also influenced the pH dependent kinetics. The validity of this model was observed as ±0.5Lmin^-1. Little variation (±10%) of the base value of constants used in GIM was observed in sensitivity analysis. It was also found out that up to 10% (v/v) of CO₂ is required for this model and beyond this CO₂ concentration, effective growth rate leads to decline phase.

References

Çelekli, A., Balcı, M. and Bozkurt, H. (2008). Modelling of Scenedesmus obliquus; function of nutrients with modified Gompertz model. Bioresource Technology, 99(18), pp.8742-8747.

Demirbas, A. and Demirbas, M. (2013). Algae Energy. Guildford, Surrey: Springer London.

Difusa, A., Talukdar, J., Kalita, M., Mohanty, K. and Goud, V. (2015). Effect of light intensity and pH condition on the growth, biomass and lipid content of microalgae Scenedesmus species. Biofuels, 6(1-2), pp.37-44.

Duan, Y. and Shi, F. (2014). Bioreactor design for algal growth as a sustainable energy source. Reactor and Process Design in Sustainable Energy Technology, pp.27-60.

Islam, M., Magnusson, M., Brown, R., Ayoko, G., Nabi, M. and Heimann, K. (2013). Microalgal Species Selection for Biodiesel Production Based on Fuel Properties Derived from Fatty Acid Profiles. Energies, 6(11), pp.5676-5702.

Juneja, A., Ceballos, R. and Murthy, G. (2013). Effects of Environmental Factors and Nutrient Availability on the Biochemical Composition of Algae for Biofuels Production: A Review. Energies, 6(9), pp.4607-4638.

MacDougall, K., McNichol, J., McGinn, P., O’Leary, S. and Melanson, J. (2011). Triacylglycerol profiling of microalgae strains for biofuel feedstock by liquid chromatography–high-resolution mass spectrometry. Analytical and Bioanalytical Chemistry, 401(8), pp.2609-2616.

Majid, M., Shafqat, S., Inam, H., Hashmi, U. and Kazi, A. (2014). Production of Algal Biomass. Biomass and Bioenergy, pp.207-224.

Moisescu, C., Ardelean, I. and Benning, L. (2014). The effect and role of environmental conditions on magnetosome synthesis. Frontiers in Microbiology, 5.

Mondal, M., Goswami, S., Ghosh, A., Oinam, G., Tiwari, O., Das, P., Gayen, K., Mandal, M. and Halder, G. (2017). Production of biodiesel from microalgae through biological carbon capture: a review. 3 Biotech, 7(2).

Natural Gas Production. (2012). Oil and Energy Trends, 37(9), pp.22-24.

Shalaby, E., El-Moneim M. R. Afify, A. and Shanab, S. (2010). Enhancement of biodiesel production from different species of algae. Grasas y Aceites, 61(4), pp.416-422.

Shao, X., Mugler, A., Kim, J., Jeong, H., Levin, B. and Nemenman, I. (2017). Growth of bacteria in 3-d colonies. PLOS Computational Biology, 13(7), p.e1005679.

Sharma, K., Schuhmann, H. and Schenk, P. (2012). High Lipid Induction in Microalgae for Biodiesel Production. Energies, 5(5), pp.1532-1553.

Sharma, N., Aggarwal, A., Eastwood, P., Gupta, T. and Singh, A. (2019). Air Pollution and Control. Springer.

Sharma, N., Aggarwal, A., Eastwood, P., Gupta, T. and Singh, A. (2019). Air Pollution and Control. Springer.

Singh, S. and Singh, P. (2019). Effect of CO2 concentration on algal growth: A review.

Tjørve, K. and Tjørve, E. (2017). The use of Gompertz models in growth analyses, and new Gompertz-model approach: An addition to the Unified-Richards family. PLOS ONE, 12(6), p.e0178691.