1Faculty of Computer and Information Technology FCIT University of Jeddah Jeddah, Saudi Arabia KSA
2Faculty of Computer and Information Technology FCIT King Abdul-Aziz University KAU Jeddah, Saudi Arabia KSA
Corresponding author Email: maaabdullah@kau.edu.sa
Article Publishing History
Received: 12/11/2018
Accepted After Revision: 29/12/2018
Today there is massive applications that generate high volume of stream data like telecommunication systems and others. In this context, it is required to convert these data to valuable knowledge. Storing data stream to local storage and mining them can be considered as resource consuming process. Mining data streams means extracting valuable information and knowledge from continues data. This paper develops Adaptive sliding window random decision Tree (ASWRT). This model can learn adaptively from the changing data especially real time data that’s related to the wireless sensors networks. The results of this research based mainly on the idea of data segmentation. This technique is one of the primary tasks of time series mining. This task is often used to generate interesting subsequence from a large time series sequence. Segmentation is one of the essential components in extracting significant patterns from time series data which may be useful in identifying the trend and changes in the prediction. The segmentations at ASWRT is mainly depending on mean and variance. The random decision tree has been employed as incremental builder for the tree for the purposes of classification. Other components to improve accuracy has been employed like sliding window-based algorithm and concept drafting detectors. ASWRT has achieved high accuracy and time performance over huge volume of data stream. These data generated by built-in random generator in MOA package. It achieved accuracy of 98.75% at time of 17.20 second in general.
Big Data; Data Stream; Stream Mining; Concept Drifting, Sliding Window
Almalki E, Abdullah M. Random Tree Data Stream Classifier with Sliding Window Estimator and Concept Drift. Biosc.Biotech.Res.Comm. VOL 12 NO1 (Spl Issue February) 2019.
Almalki E, Abdullah M. Random Tree Data Stream Classifier with Sliding Window Estimator and Concept Drift. Biosc.Biotech.Res.Comm. VOL 12 NO1 (Spl Issue February) 2019. Available from: https://bit.ly/2L1zs1j
Introduction
Due to the high informatic evolution, there is a huge volumes of data stream these data collected from different resources like sensory data, transactional, and web data. These data generated in continuous manner as data stream. This type of data requires to be analyzed online as they arrive without storing them and wasting high amount of memory. Big data can be constructed from data streams. Big data is defined as large and complex data sets where traditional data processing are inadequate to process. Challenges in big data include many issues, such as analysis, capture, search, sharing, storage, visualization, querying, updating, and information privacy. The term “big data” often refers simply to the use of predictive analytics, user behavior analytics, or certain other advanced data analytics methods that extract value from data. Big Data can be static on one machine or distributed and it can also be dynamic (stream). Data stream is considered as an ordered sequence of instances that can be read only once or a small number of times using limited computing and storage capabilities. Data stream is continuously changing based on time and this is considered as big challenge in the field of data stream mining. Stream mining is the process of extracting knowledge structures from continuous, rapid data records.
A data stream can be collected from computer network traffic, phone conversations, ATM transactions, web searches and sensor data. Data stream real time analytics are needed to manage the data currently generated at an increasing rate. In the data stream model, data arrive at high speed, and algorithms that process them must do so under very strict constraints of space and time. Consequently, data streams pose several challenges for data mining algorithm design like using of limited resources (time and memory). The data stream mining model can be implemented using many tools depending on the environment. This research will focus on MOA (Massive Online Analysis). MOA is a software framework that can be used to implement and run the streaming algorithms. It can be considered as open source framework for data stream mining. It has many of machine learning algorithms classification, regression, clustering, outlier detection, concept drift detection and recommender systems and tools for evaluation, [2].
The process of designing data stream mining model is subjected to several conditions like results accuracy, amount of space consumed by the model and time consumed in learning this model. These conditions are mainly interdependent where the time adjustment and space used by the algorithm may reflect high change in accuracy. In addition, storing more pre-computed information, such as look up tables, an algorithm can run very fast at the expense of space consuming. The more time an algorithm has, the accuracy can be increased. In data stream environment, the developer should take care of time and space due to the high speed and the huge volume of data. In this research, a novel model has been developed which considered the memory space and time constraints by adopting the concepts of data estimation and concept drift. Due to speed of the input data, some changes may happen to the data. These changes happened due to some problem in the networking, synchronization or accumulative error by time passing. These changes would affect the classification negatively and would cause misanalysis of data. Data estimation is abstraction of data and also it is considered as the step of preparing and packaging the input data stream in order to facilitate the process of classifier, while concept drift is the process of detecting the change in the data stream and inform the estimator to refresh data and consequently the classifier will perform some actions in the presence of drifting.
The rest of this research is organized as follows: first of all, some related works will be discussed, after that the general structure and all components of ASWRT proposed model will be explained and discussed. Finally, the model will be tested and analysed depending on several criteria as can be seen later
Related Work
Concept drifting means a change in the statistics of the data which happens due to different factors such as network synchronization or cumulative error done by the estimators. To avoid the effective of the concept change, there were many algorithms and models related to the subject of concept drifting. Last in [10] introduced a classification for a system incorporate the info fuzzy network (IFN) for OLIN (On Line Information Network) classification. OLIN input is continuous stream data, and the model is responsible for building a network. This network mainly depends on a sliding window as estimator of the most recent data. The system continuously will changes the window size and all statistical variable recomputed depending on the current rate of concept drift. OLIN uses the statistical ratio of the difference between the training model and the accuracy of the current model to measure the concept stability. OLIN will adjusts the number of examples between model reconstructions continuously. OLIN also generates a new model for every new sliding window depending on the content of the window. This approach ensures accurate and relevant models over time and therefore an increase in the classification accuracy. However, OLIN algorithm has very important disadvantages which is the high cost of creating new model each time.
Hulten, et.al have come up with Concept-change Very Fast Decision Trees CVFDT. It is considered as an algorithm extension for VFDT to deal with concept change over decision tree. This algorithm allows to the model to learn in the same time of determining the concept change. This sycron can be achieved by continuously monitoring the accuracy of old decisions with respect to the content of the sliding window of data [1]. At [2] the researchers proposed model for building incremental decision tree by adopting the sliding window and using change detector. The window has been built linearly, depending only on the average of inputs. The main advantage of using a change detector is that it has theoretical guarantees, and this guarantee can be extended to the learning algorithms.
Data Stream Mining Framework
In the field of stream mining, mostly all algorithms adopted one or more of the following components [2]: windows for keeping the most recent values; mechanism to control the distribution change; and finally method for keeping updated estimations for some statistics of the input. These three modules are considered as the basis for answering three of the most important questions in stream mining.
- What should be remembered or dropped
- When to do the model refresh, and
- How to do this refreshing.
Three components are essential to prepare data streams for stream mining process. As shown by figure 1, Xt is a stream of bits representing data to be classified. Estimator is the component of the model that’s responsible for computing all the statistics on the input data and preparing data inside the window. The last component is the detector which is responsible for detecting the place of drifting. The idea at this research is done by basing the mining algorithm on sliding window. The next two subsections detail concepts of estimator and concept drift.
![Figure 1. General framework [Mala & Dhanaseelan, 11]](http://bbrc.in/wp-content/uploads/2020/11/fig1_fmt-1.jpeg) |
Figure 1: General framework [Mala & Dhanaseelan, 11] |
Estimators
The estimator is considered as numerical value of unknown parameter by applying some formula on limited population samples. High volume and open-ended data streams need processing methods [7] presents a series of designed criteria. The most important of these criteria are:
- The consuming time needed by the mining algorithm to process each data record in the stream must be small and constant
- Smallest main memory wasting
- Due to the nature of data stream, it should be a single pass algorithm, since streams cannot be hold for long time.
- The model availability.
- The model must show updated results at any point in time, it must keep up with the changes of the data.
The above criteria are important to build an adaptive learning model, but the first two criteria can be considered as the most important and hard to be accomplish. Although many algorithms have been done on scalable data, most algorithms still require high amount of main memory in proportion to the actual data size. Their computation complexity is much higher than linear with the data size. So, they are not equipped to cope with data stream [6].
The best way to avoid wasting memory is to use estimator that estimates the behavior of the data stream depending on limited data. There are many types of estimators according to its purposes like liner estimators, blue line estimators [3] and Gaussian estimator [12]
Change Detectors
Traditional stream classification algorithms developed to find classes that are suitable for all points since the beginning of data. These types of algorithms do not reflect the important issues that’s related to the concept drifting. Concept drift can be considered as critical problem in online learning. This problem is caused when a model based on old data cannot correctly reflect the current state of the data. Concept drift describes a gradual change of the concept where concept shift happens and when a change between two concepts is more abrupt. Distribution change [8], also is known as sampling change or shift or virtual concept drift [1]. It refers to the change in the data distribution. Even if the concept stays the same, the change may often lead to rebuild the current model as the model’s error rate increased. Stanley [13] has suggested, from the practical point of view that it is not essential to differentiate between concept change and sampling change since the current model needs to be changed in both cases. Change detection is not an easy task, since a fundamental limitation exists in [5], the design of a change detector is a compromise between detecting true changes and avoiding false
alarms.
Aswrt: Adaptive Sliding Window Random Tree
This research proposes a general method for building incrementally random decision tree based on keeping sliding window of the last instances on the stream. In order to clarify the idea, we should specify how the following requirements should be done:
- Place a change detector related to every node that’s make an alarm if some change happened at that’s node.
- Manage the process of creation and deleting of nodes in the tree
- Maintain estimator of the relevant statistics of every node that’s related to the current sliding window.
Adaptive Sliding Window Random Tree ASWRT is a model performing data stream classification. It is based on three data stream components that’s mentioned earlier. The first component is the estimator and it is responsible for preparing and estimating the statistics of the input data. Second component is the classifier, the classifier here is random decision tree that’s build incrementally depending on the coming streams. Last component is the detector to keep the data updated and consistent. Figure 2 shows ASWRT model.
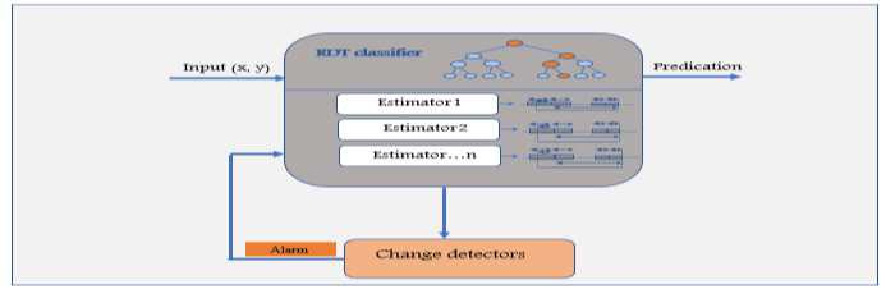 |
Figure 2: Adaptive sliding window Random Tree (ASWRT) |
In general, the input to this algorithm is a sequence x1,x2,…, xt,… of data items whose distribution varies over time in an unknown way, the range of input values is [0,1] values or real value that can be rescaled later by the model. The complete transaction that’s happened inside the model is depicted in algorithm 1.
From the architecture, an estimator uses mean and variance of the inputs to estimates the desired statistics. Then it prepares data into bucket inside the window. A copy of the window will be send to the classifier and another copy to the change detector in order to detect the changes in the concept of data. If a change is detected, the last added buckets will be removed from the window and the affected added subtree will also be removed.
Algorithm 1: Adaptive Sliding Window Random Tree (ASWRT)
Input: stream xt generated by random tree generator
Output: classified input, accuracy of classification and Time
Call Estimator
preparing data in buckets depending on some criteria see algorithm 1
Call change detector
Determine whether change in statistics occur or not and making alarm to the estimator if the change in concept occurred see algorithm 3
Call DM algorithm
Making the classification depending in the data that’s produced by cooperating of Estimator and detector, in order to determine time and accuracy of classification the next steps should be followed:
- Train the model over prepared set of data which is training set
- Test the model using deferent data set to check the time and accuracy of the model
ASWRT Estimator
The process of building and reducing the sliding window depends on some statistical distribution computation especially mean µ and variance ó. The idea here is done by segmented all elements of data stream into buckets by algorithm 2. For each bucket Bi, a time stamp should be maintained. ASWRT model will be responsible about determining the following information which are: how many elements enter the bucket, the mean of these bucket and the variance. The mean of the elements in the bucket (µi), and the variance of the bucket (Vi). The actual data elements that are assigned to a bucket are not stored.
As shown with figure 3, the window will be initialized at particular time stamp and it has a fixed size. Inside the window, data will be segmented to number of buckets with elements (ni). Now let the most recent element denotes xt, so xt elements are inserted to the window. This element has time stamp t. So, at this time, the estimator has several cases. The first case is when xt = µ1 & ó1, this means that the arrived element has the same distribution parameter as of the current bucket. So, estimator extends the current bucket B1 to include xt. Otherwise, create a new bucket for xt. The most recent bucket becomes B1 and set new variance and mean for this bucket as ó1 = 0, µ1 = xt, n1 = 1. The old bucket will be incremented by 1 (Bi+1). The second case, if the oldest bucket Bi has timestamp greater than N, actual window size, then delete the bucket. Bucket Bi−1 becomes the new oldest bucket. Maintain the statistics of Bi−1* (instead of Bi*). The third case is occurring when connecting with Adaptive Sliding Window ADWIN change detector. In this case if change detected, then ASWRT drops the first bucket from the head of the window Bi-1.
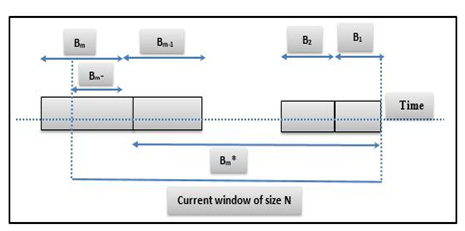 |
Figure 3: Visual explanation for the estimator steps |
Algorithm 2: Estimator of ASWRT
Input: xt the new arrived element
- If xt= µ1, then extend bucket B1to include xt, by incrementing n1 by 1.
- If xt! = µ1then create another bucket for xt. The most resent created bucket becomes B1with ó2 = 0, µ1 = xt, with size n1 = 1. An old bucket Bi becomes Bi+1.
- “If the previous bucket which is Bmhas timestamp greater than the time stamp of N, the bucket will be deleted. Bucket Bm−1becomes the new oldest bucket. Maintain the statistics of Bm−1 instead of Bm, which can be calculated by the statistics of the previous deleted bucket Bm and the statistics of current oldest bucket which is Bm−1. the calculation in the next step.
- If two buckets have been combined then the statistics of the new combined bucket will be as follow:
- if there is an alarm detected by the detector the drop the Biand recalculate the statistics of Bi-1depending on previous Bucket statistics Output: ordered sequence of bucket inside window with its statistics see figure 3
![]()
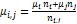
![]()
ASWRT Detector
In the proposed ASWRT model, ADWIN change detector [8] is adopted to detect the concept drift. The sliding window is adopted here to reduce the stale in data. In the window model the data stream will coming in continuous manner, only the most reacent part of data will be used for making the predications. The process of discounting the size of the window only happened by fixed parameters, that’s why the results of the estimators vary according to this parameter. In this case every data elements are associated with weights that decrease over time. Here, only the last N elements arrived are considered relevant for answering queries, where N is the window size [2].
ADWIN model is an adaptive sliding window algorithm that has an estimator with memory and change detector and is considered as a parameter-free adaptive sliding window. This means no fixed parameter for the window size [12].
Results and Analysis
At this section, results of ASWRT will be shown depending on specific methodology. This methodology depends on the process of adjustments of the parameters that can affect the time and accuracy. Time is considered as the most important signal about the goodness of the model due to the nature of streaming environment as well as the accuracy. ASWRT will considered as good model in data stream mining if it satisfies high accuracy in minimum time.
The experiment here will be done depending on many steps. These steps is determined by adjusting the parameters of classifier and analyzing the impact of this adjustment. The adjustment will be performed depending on the following parameters
- Number of attributes.
- Number of instances.
- Number of classes.
The results of testing ASWRT model start by adjusting the first parameter which is the number of instances and the other parameters is adjusted to the default values. These default values are shown in table 1
| Table 1: The Experiment Default Values | |
| Experiment parameters | Default values |
| Number of instances | 500,000 |
| Number of classes | 3 |
| Number of attributes | 10 |
| Number of passes | 1 |
| Model Random seed | 1 |
| ADWIN thresholds | 0.05 |
| First leaf level | 3 |
Impact of increasing the number of instances on ASWRT
At this section, ASWRT will be examined by adjusting the number of instances to see their impact on the accuracy and time. The number of instances in this experiment ranges from 100,000 to 1,800,000 instances, while the other values have its default values. It is observed that the accuracy of classification is increased from 92.60% at 100,000 instants to 98.88% at 1,800,000 instants, as shown in figure 4. It can be noticed that the accuracy becomes constat after 1,400,000 instants. The time result records 3.3s at 100,000 instants and 18.8s at 1,800,000. We can also witness that the constant test time, along with the increase of instances. Figure 4 and 5 show strongly increasing in accuracy and slightly linear increase in train and test times.
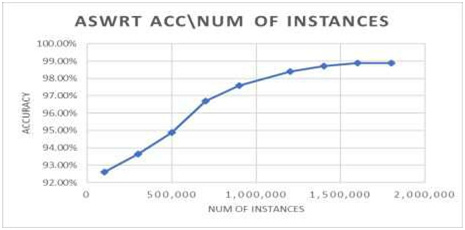 |
Figure 4: Impact of increasing the number of instances on accuracy |
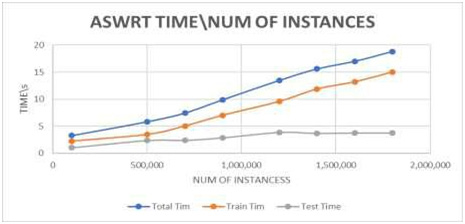 |
Figure 5: Impact of increasing the number of instances on time |
Impact of increasing the number of classes on ASWRT
In this section, the results of ASWRT has been shown with respect to the number of classes. The number of attributes and instances will be of the default values. Increasing number of classes shows an inverse relationship to the performance of the algorithm. ASWRT increases the number of classes from 2 to 8 classes. Here the number of attributes are 10 attributes, which is the default number for this parameter. The accuracy of classification is decreased from 95.51% at 2nd classes to 88.63% at 8th classes. Figure 6 and figure 7 show accuracy and time when increasing number of instances.
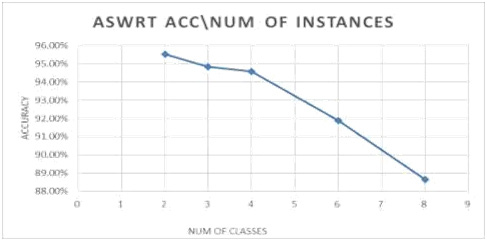 |
Figure 6: Impact of increasing the number of classes on accuracy |
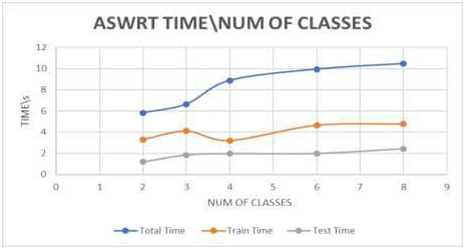 |
Figure 7: Impact of increasing the number of classes on Time |
Impact of increasing the number of attributes on
ASWRT
In this section, the impact of increasing the number of attributes on the proposed model are studied. All other values adjusted to the default values. The model records accuracy of 98.78% at 5 attributes and 93.70% at 25 attributes the results of accuracy and time are shown in figure 8 and 9. ASWRT records high accuracy even if the number of attribute increased to 25 attributes. This result is considered as positive indicator about the quality of the model.
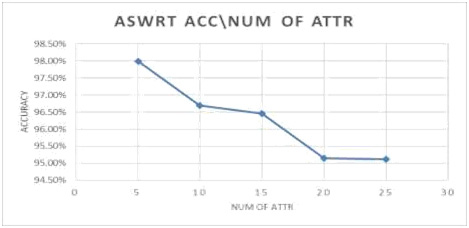 |
Figure 8: Impact of increasing the number of attribute on accuracy |
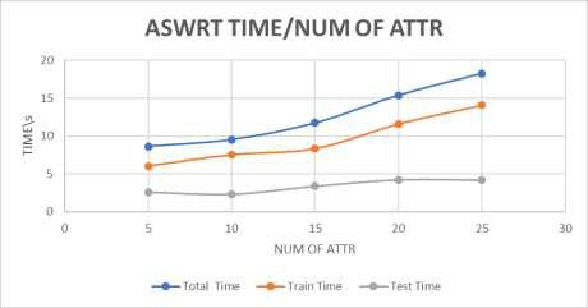 |
Figure 9: Impact of increasing the number of attribute on time |
Comparing Aswrt with Other Models
A comparison will be made between ASWRT model and other models to see its performance related to state of the art models. These models adopt linear estimator for estimating all statistics of the input and using ADWIN and DDM change detectors [8]. The DDM module will manage errors that’s produced by the learning model in the step of prediction. It will compare the statistics of two sub windows: the first window contains the actual data, while the second will contains only the data from the beginning until errors increases. Their method does’t store these windows in stored in memory .They consider the number of errors in a sample of examples is modeled by a binomial distribution .when the number of errors increased the algorithm will prpose thats the distrbution is changed, and the current model decsions are inappropriate. Two classifiers have been chosen for this experiment which are naïve Bayes (NB) and adaptive Hoffding tree classifier (AH). These models have been tested by running their codes, the code has been imported from Waikato websites [2]. As shown in table 2, ASWRT and AHT classifier give more accurate results compared to the naïve Bayes in both cases. While AHT and ASWRT show a proximity result with preference to ASWRT, the result depending on the running the three-models using MOA using default values for all parameters. Figure 10 shows the accuracy of the three models, ASWRT shows the highest accuracy among others. While in case of time as shown by figure 11, ASWRT recorded acceptable time.
| Table 2: The Result of Comparing ASWRT with Similar Works | |||
| Model | ACC (%) | Total Time(s) | Kappa stat (%) |
| ASWRT-ADWIN | 95.793% | 8.42s | 91.369% |
| ANB-DDM | 73.704% | 6.77s | 49.527% |
| AHT-ADWIN | 88.43% | 6.70s | 83.652% |
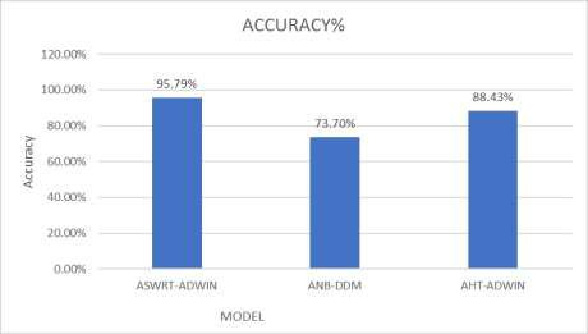 |
Figure 10: The accuracy of different adaptive model for classification |
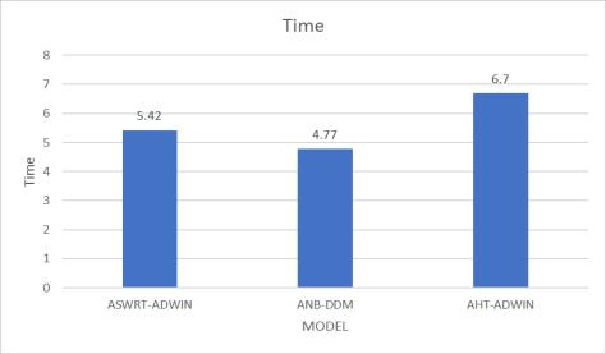 |
Figure 11: The run time of different adaptive model for classification |
Conclusion and Future Work
This research has concentrated on developing a novel model in the field of data stream mining which is ASWRT. This aim has been achieved by applying two contributions; the first one is the process of developing algorithm for the adaptive sliding window. This algorithm has a several cases depending on type of data streams as discussed in algorithm 2. The output of this algorithm is ordered sequence of buckets inside the window. The second contribution was to apply drift detection process using ADWIN change detectors. The detector will cooperate with the estimator in case of drifting and the classifier also have been modified in case of drift by eliminate the affected leaves in the tree which may reduce the accuracy of the classification. The evaluation of the results was depending on two factors which are accuracy and time. The testing methodologies was depending on the adjustment of some parameter related to the classifier to see the impact of this adjustment on the time and accuracy. In near future some extra functions can be increased like multi-labelling and detecting outlier to make a complete model and the developer should care of time because the time increase by increasing the number of computations. Also, same model can tested in case of increasing the data throughputs and analysing the results.
References
- Aggarwal, C. C. A framework for diagnosing changes in evolving data streams. Paper presented at the Proceedings of the 2003 ACM SIGMOD international conference on Management of data
- Bifet, A. & Kirkby, R.: Data stream mining a practical approach.
- Gama, J., Sebastião, R., & Rodrigues, P. P. Issues in evaluation of stream learning algorithms. Paper presented at the Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining.
- Giannella, C., Han, J., Pei, J., Yan, X., & Yu, P. S.: Mining frequent patterns in data streams at multiple time granularities. Next generation data mining, 212, 191-212.
- Gustafsson, F., & Gustafsson, F.; Adaptive filtering and change detection (Vol. 1): Wiley New York.
- Heinz, C.: Density estimation over data streams.
- Jiang, N., & Gruenwald, L.; Research issues in data stream association rule mining. ACM Sigmod Record, 35(1), 14-19.
- Kifer, D., Ben-David, S., & Gehrke, J.; Detecting change in data streams. Paper presented at the Proceedings of the Thirtieth international conference on Very large data bases-Volume 30.
- Lakshmi, K. P., & Reddy, C.; A survey on different trends in data streams. Paper presented at the Networking and Information Technology (ICNIT), 2010 International Conference on
- Last, M. Online classification of nonstationary data streams. Intelligent data analysis, 6(2), 129-147.
- Mala, A., & Dhanaseelan, F. R.; Data stream mining algorithms: a review of issues and existing approaches. International Journal on Computer Science and Engineering, 3(7), 2726-2732.
- Mossel, E., Olsman, N., & Tamuz, O.; Efficient bayesian learning in social networks with gaussian estimators. Paper presented at the Communication, Control, and Computing (Allerton), 2016 54th Annual Allerton Conference on.
- Stanley, K. O.; Learning concept drift with a committee of decision trees. Informe técnico: UT-AI-TR-03-302, Department of Computer Sciences, University of Texas at Austin, USA.


