¹Department of Environmental Engineering, Graduate School of Environment and Energy, Science and Research Branch,Islamic Azad University, Tehran, Iran

²Department of Environmental Engineering, Faculty of Environment and Energy, Science and Research Branch,Islamic Azad University, Tehran, Iran

³Department of Environmental Engineering, Faculty of Environment and Energy, Science and Research Branch, Islamic Azad University, Tehran, Iran

⁴Department of Environmental Engineering, Faculty of Environment and Energy, Science and Research Branch, Islamic Azad University, Tehran, Iran

Corresponding author Email: far-atabi@jamejam.net

Article Publishing History

Introduction

Today the occurrence of environmental, hygienic and security harsh events caused by the release, ignition, and explosion of chemical and toxic materials in different industrial units has necessitated the more than before preparation for prevention or confrontation with these dangers and accidents. So the places disposed the diffusion and the dangerous material consistency are equal or more than the fatal or dangerous materials there can be recognized through prediction and material diffusion quality modeling before the event occurrence and reduce the amount of financial, vital and environmental damages through appropriate engineering and managing techniques in emergency conditions and crisis management plans at the time of event outbreak, (Siddiqui et al. 2012).

In this regard, Yoshihito Tominaga proposed his study, mentioned that Near-field pollutant dispersion in the urban environment involves the interaction of a plume and the flow field perturbed by building obstacles. In the past two decades, micro-scale Computational Fluid Dynamics (CFD) simulation of pollutant dispersion around buildings and in urban areas has been widely used, sometimes in lieu of wind tunnel testing (McBride et al. 2001). Key features of near-field pollutant dispersion around buildings from previous studies, i.e., three-dimensionality of mean flow, unsteadiness of large-scale flow structure, and anisotropy of turbulent scalar fluxes, are identified and discussed. It is important to choose appropriate numerical models and boundary conditions by understanding their inherent strengths and limitations, (Sklavounos, and Rigas,
2004).

One of the first studies in which CFD used to simulate emission of gases, the studies by Sutton et al.,(1986) can be mentioned, that they used k-å Turbulence model to consider viscosity effects of turbulence. Using these instruments faced with progress at computer hardware. Perdikaris stated in this context that computational fluid dynamics (CFD) has been recognized as a potent tool for realistic estimation of consequence of accidental loss of containment because of its ability to take into account the effect of complex terrain and obstacles present in the path of dispersing fluid (Gavelli, et al., 2008). In this paper an attempt has been made to employ CFD in the assessment of heavy gas dispersion in presence of obstacles ( Hong-xi, et al., 2008).

Some workers have stated safety reports required for sites storing quantities of dangerous substances in excess of specified levels should include an assessment of the risk associated with the facility, which will include an evaluation of the effects of releases of dangerous substances to the environment. The models commonly used for assessing the dispersion of dense gases in the atmosphere are based on the unobstructed terrain. They have proposed physical modeling of releases in a Boundary Layer Wind Tunnel (BLWT) and the use of Computational Fluid Dynamics (CFD).

These papers focus on the key findings of the study, which provide a dramatic insight into how terrain and buildings can fundamentally alter the dispersion behavior of dense gases. The results show how flat terrain models may overestimate the chlorine hazard range by as much as a factor of 5, whilst the predicted direction of travel of the cloud may err by up to 90 (Alberto and Hill, 2008). Kashi et al., (2009) in a study entitled “Temperature Gradient and Wind Profile Effects on Heavy Gas Dispersion in Build up Area”, stated dispersion of heavy gases is considered to be more hazardous than the passive ones. This is because it takes place more slowly. In this paper, based on the extensive experimental work of Hanna and Chang, the CFD model was tested compared with Kit Fox experiments. In order to accomplish this validation, the multiphase approach was employed as a new method in this area. In addition, the temperature gradient effects were investigated. The survey of wind speed was done taking factors such as time, height and direction into the consideration. To reduce the number of elements in computational domain, a combination of 2D and 3D geometries were utilized (Kashi, et al.
2009).

This paper deals with the evaluation of the atmospheric dispersion CFD tool Fluid-PANACHE against Prairie Grass and Kit Fox field experiments. A description of the models for turbulence generation and dissipation used (k–3 and k–l) and a comparison with the Gaussian model ALOHA for both field experiments are also outlined, (Cormier et al. 2009).

As observed, many researchers provided a variety of studies on accuracy of different turbulence models in predicting emission. Study by Zhang et al. (2009) and Gavllei in 2010 can be remembered here. Zhang has used k-å model to model gas emission with density over air. The results of their study to the experimental results found with acceptable error 2.2%. Currie et al. in 2012 using CFD examined how a heavy gas dispers in an area and addressed evaluating risk regarding the results (Zhang, 2009).

Given the progress in software and hardware contexts particularly at the recent decade, using CFD to predict how the pollutants emit at residential and industrial areas has been increased. Indeed, CFD and/or modeling flow in a three-dimensional form is as a virtual laboratory in which effect coming from different parameters on flow can be examined easily with very low costs rather than experimental methods like real measurements, (Gavelli et al. 2010).

Materials aσnd Methods

Three-Dimensional Simulation Algorithm

To simulate using CFD, the specific stages for simulation process have to be paved and such stages dependent from type and geometry are simulated, and they have shown in figure 1.

Figure 1: Total procedure for simulation process using CFD

One numerical method to resolve integral form of prevailing equations is the Finite volume or the control volume. In this method, the physical amplitude is divided to small volumes and the dependent variables are measured at the center of volumes or in corners. Equations resolving at the computational area regarding the physical conditions of field are the very Conservation equations of mass and momentum. Further, to simulate disturbance of flow, transmission equations are resolved for turbulence flow. This study aims to achieve ammonia concentration at different times and places at computational area. Thus, species conservation equation has to be resolved at these problems. In following, a summary of these equations has been addressed.

Species conservation equation is written as follows:

K	C1	C2	Cμ	σ1	σ2
0.3875	1.68	1.42	0.085	0.7179	0.7179

 

 

 

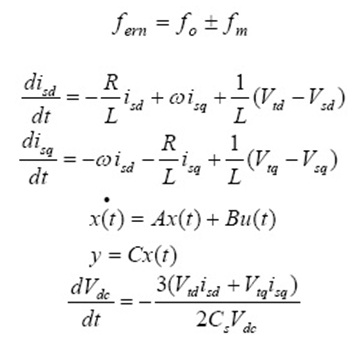
Where σand ui are fluid density and components of average speed.

The equation of motion extent and/or momentum at direction i is written as follow:

In expression above, p, ô_ij, pg_i are Static pressure, Stress tensor and Physical force of gravity in direction of i. in expression 2, stress tensor is defined as expression 3. In expression 3, µ is molecular viscosity of the fluid and µ is not of the features of fluid, and is defined entitled Shear viscosity in turbulent flows.

 

 

 

 

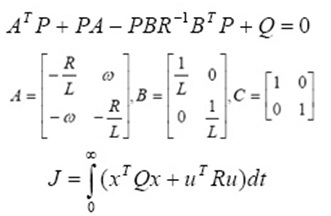
Yakhot et al. proposed a new type of k-å model in which functional features and characteristics compared to standard model reported. The proposed model based on renormalized group theory reported so-called RNG. RNG k-å model in its physical form is similar to standard model.

General form of equations at RNG k-å is as follows:

 

 

 

 

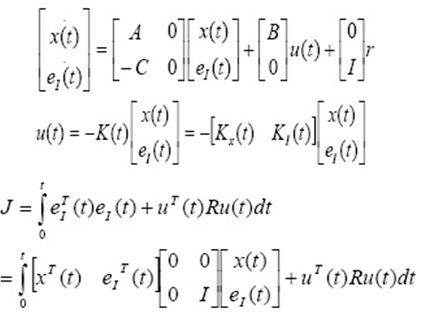
In equation above, the additional term contains ç parameter, indicating Characteristic time of turbulence
Characteristic time of the flow field. Hence, model of off-equilibrium effects have been also considered.

The main coefficients of model RNG for Isothermal flows include: ñ_å, ñ_k, C₁, C₂, and C_µ. Two other coefficients, that is, ç₀ and using these coefficients and Von Karman constant K are obtained. The coefficients below are the ordinary coefficients used in this model.

Table 1: features of wind profile
Wind speed at the reference height(m/s)	Roughness of surface(m)	λ
1.9	0.005	0.07

ç₀ and are obtained using the coefficients below:

Table 2: Values of mi, mass flow and the volume of gas released
Total Released Volume (m3)	Total Released Mass (kg)	Mass Inflow Rate (kg/s)
1970	4767	3178

 

 

 

 

 

 

 

 

 

 

Modeling of Thorney Island real experiment through CFX software based on CFD method:

In this study, the results of Thorney Island experiment have been used for estimation of CFX amount of accuracy that computes and models based on CFD method.The first phase of field experiments to spread heavy gas dispersion trials at Thorney Island associated to release of gas in an area without barrier considered, yet the second phase of experiments aimed to examine heavier gas dispersion than air in surrounding barriers.

In the experiments associated to a barrier, a cube 9m × 9m × 9m, which was made of wood and plastic sheets the trailers for moving obstacle and put it in the proper position has been used; further, a trailer to displace barrier and place it in proper positions have been used. Gas supply cylinder (actually a 12-sided) with a diameter of 14 meters and a height of 13 m, and a volume of 2000 cubic meters reported. In this part of the project of Ammonia, Test Results for Project No. 26 Thorney Island for assessment and verification of CFD has been used. In this experiment, a cube barrier in distance placed 50 meter lower than cylinder. Ga mixture containing 68.4% nitrogen and 31.6% Freon mentioned that during this experiment, the wind speed has been measured approximately 1.9 m/s.

Table 3
Temperature	30 C0
Wind speed	9.78 m/s
Sustainability class	D
Flow angle relative to the Z axis	8 degree
Flow disturbance intensity	5%

Geometry modeling and networking

Computational area in this modeling considered 150m × 100m × 40m cube dimensions. Due to the geometry and the symmetry with respect to the symmetry passing through the center of the cube, the flow in symmetrical regarding boundary conditions is solved. In figure 2, the networking has been shown.

Figure 2: Networking computational fi eld of Thorney Island

Applying boundary conditions

Wind input flow

Wind speed is one of the most important factors in the spread and dilution of gas, and transmitted gas to different parts of the range. If wind speed taken in a defined height, then the speed profile using exponential expression can be expressed as follows:

Where ë is a dimensionless value and its value relies on the extent of sustainability and also roughness of dependant surface. Given the experiment conditions No 26, values of ë and roughness have been represented in table 1 as shown below.

 

 

 

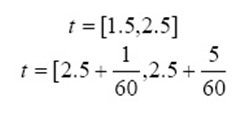
Gas input

According to the experiment no 26, about 2000 m³ of gas mixture at lower than 1.5 second is released at atmosphere to enter the boundary conditions at Transient state of mass flow rate, the gas mixture is defined through Step Function.

 

 

 

Where mi has been defined in table 2.

Walls

In the course of solving the steady state, barrier and cylinder are taken into account, and in the course of solving Transient state, barrier with the condition of the walls is considered. Furthermore, the ground surface is specified with the wall boundary condition. To the earth surface, the roughness of surface with 0.005 meter, and to the barrier and cylinder, the supposition of the smooth surface is used.

Symmetry boundary condition

As mentioned, the plane of symmetry passing through the center of the cube as the Symmetry boundary condition is considered. Furthermore, upper and lateral surfaces given that taken sufficiently far from barriers, and the flow would sustain steady at this area, are defined with Symmetry boundary condition. In general, Symmetry boundary condition causes the gradient perpendicular to the surface with different components at flow field taken equal to zero.

Results and Discussion

The flow in nature in this problem taken as a transient flow; to resolve transient flow, all the time considered for modeling, time steps and early conditions have to be taken as the input. To determine the early conditions, in initial the flow has to be resolved in steady state and its results have to be applied as the early conditions so as to resolve the transient flow. In initial, the results of stationary status were entered into discussion and later the results associated to the transient flow have been discussed as well.

The results of steady flow

In figure 4, the flow lines in the plane of symmetry passing through the center at the computational area have been shown. As expected, separation of flow and building Vortices behind the barriers can be seen. In figure 5, Eddie Cantor frequency has been shown. As observed, at most areas, this frequency placed at the area 1 Hz. As a result, the time interval for Eddies at 1 second placed, that this makes the comparison between experimental results and numerical results possible.

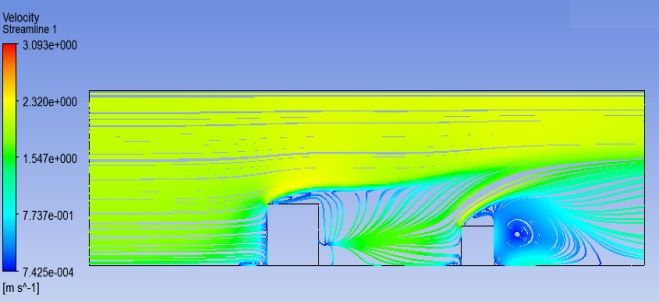Figure 3: Flow lines for steady status

 

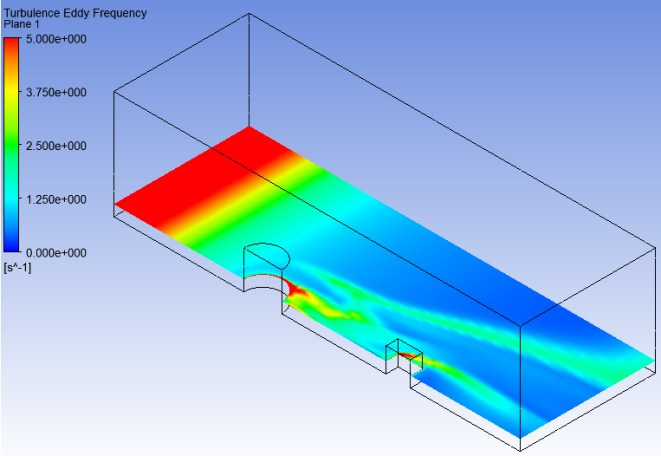Figure 4: Eddie Frequency disturbance

 

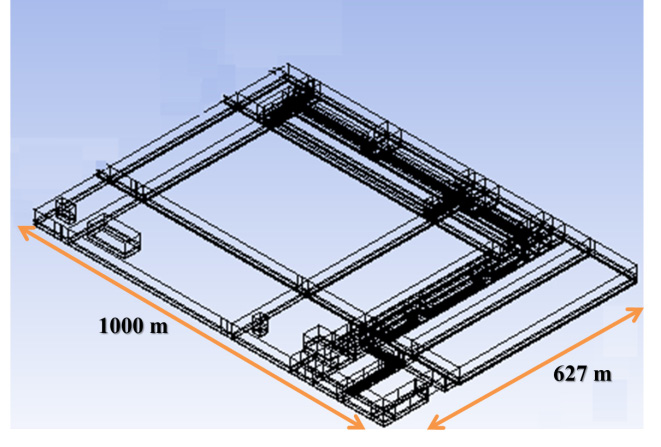Figure 5: Dimensions of computational area

Numerical analysis of ammonia leakage effect from one of the ship tanks carrying ammonia in one of Iran’s South Pars dock located in Asalooye area

This part of study aimed to provide numerical simulation for ammonia leakage at one of Iran’s South Pars dock located in Asalooye area. After ammonia produced at Petrochemisty and distance about 1.5 km passed through output Pipeline from petrochemical producers of ammonia, this substance reaches to loading area at the considered dock in a liquid form. This dock is particularly for loading ethylene, butane, propane and ammonia. The capacity of ships varied from 15 to 40 thousand tons. Modern ships used today to prevent leakage are such two-walled vessels. Also, a ship to be capable of carrying different types of liquid product or when damaged or leak to any fluids loaded to be lost, so such a ship is required to be provided with different loading tanks.The ship under study in this research contains 10 tanks. Since, possibility to damage to ships and leakage at them might come to realize at least in one of the ship tanks, thus modeling ammonia emission deriving from collapse of one ship tank aimed in this project. In following, how to simulate as well as the results have been proposed.

Geometric modeling and networking

According to the data given by Operations and Productivity, in average loading ships contain 10 tanks with 2000 m3, and as a result 10 Spherical tanks by diameter of 15.5 meter have been taken into consideration. The length of ship has been taken 180 meter. In figure 9, dimensions of computational area have been proposed. As observed, this computational area includes different barriers in different forms. All the constituents existing in surrounding dock have been modeled. The computational area includes a series of Rack structures, pipelines transmission of petrochemical products, two buildings beside each of docks, the whole dock and administrative buildings.

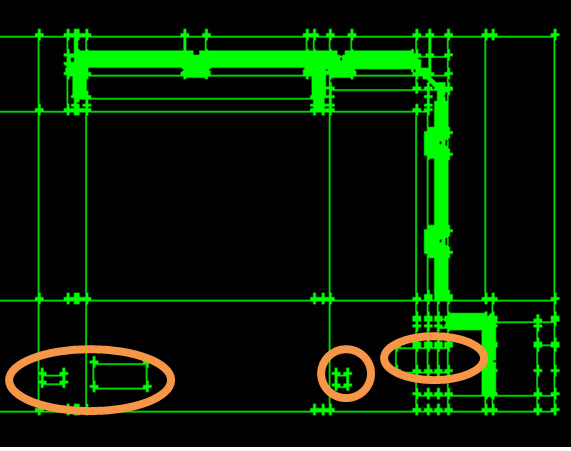Figure 6: A perspective of the upward of geometry and position of buildings

 

Figure 7: the geometry produced for Rack structure

 

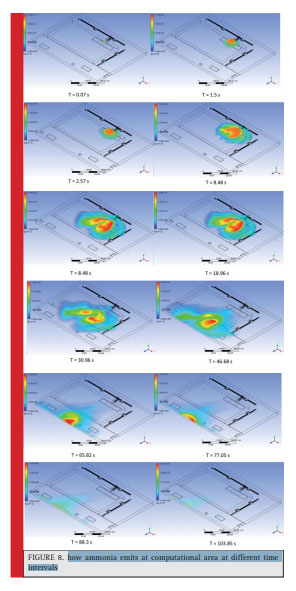Figure 8: How ammonia emits at computational area at different time intervals

 

Figure 9: Flow lines at different time intervals

 

In figure 10, the upward perspective around dock, and in figure 11, a part of geometry produced for Rack structure have been shown. In figure 10, areas specified with orange color indicate administrative buildings. One of the most optimal methods to reduce the elements used simultaneously not the accuracy at results reduced, is the very notion which lies in networking with organization. In the complicated geometries, the only way to achieve this aim is dividing the main geometry to smaller parts with the capability of networking with organization in them. For this, the computational area has been divided into 456 pats with smaller volume.

Figure 10:  fixed concentration surfaces 150 ppm defi ning ERPG2

 

Figure 11:  fixed concentration surfaces 750 ppm defining ERPG3

 

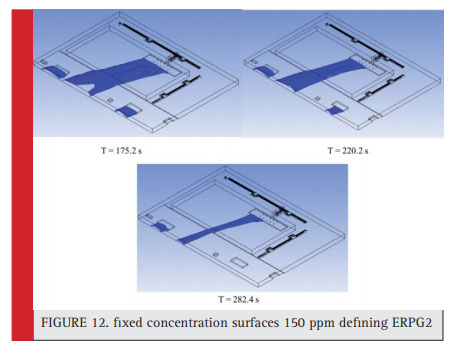Figure 12:  fixed concentration surfaces 150 ppm defining ERPG2

These blocks can be observed in figure 11. Yet, accordingly all the computational area cannot to be divided into cubic blocks, so that the only way at the remained areas would be the use of a disorganized network.

Yet in such an occasion, blocks in which disorganized network emerges are reduced; as a result, in a lower space of computational area, disorganized network has been produced. This can reduce the elements in a substantial amount. Finally, the number of networks produced would be 2893527.

Simulation using CFD

As mentioned, ship with 10 tanks mentioned with the volume of 2000 m3. To model how the ammonia entered to the area, all the ammonia existing in the tank has to enter into area. For this, it is supposed the ammonia to be entered to the area with Constant flow in a steady status and in a little time. As a result regarding the computations, it has been supposed that ammonia with flow rate equal to 78667 kg/s for 15 seconds emits through the surface of tank. The temperature of ammonia emitted equals to -33 C0, that numerical modeling has been carried out for 10 minutes. Further, the conditions of area in autumn season at the studied area have been considered. The wind speed and temperature of environment have been taken 9.78 m/s and 30 C0, respectively.

Apply Boundary Conditions

Wind flow input

According to the data associated to the meteorological stations, wind speed has taken 9.8 m/s. in table 3, the conditions acted for wind flow input have been regarded.

Wind flow output

At these surfaces, Pressure outlet boundary condition has been used. The pressure regulated equals to 1 atmospheric pressure.

Gas input

Here, a sudden collapse of ammonia tank might be faced. As a result, to model sudden dispersion of ammonia, supposed that all the mass existing in tank enter to the computational area in a 15 seconds. As a result, it emits with flow rate of 78667 kg/s. temperature of ammonia emitted equals to -33 C⁰ and Turbulence intensity
with 5%.

Symmetry boundary condition

Upward the computational area placed at a height in which the gradient for flow parameters equals to zero. As a result, the supposition to use symmetry boundary condition at this surface is an acceptable supposition. This condition considers the gradient perpendicular to this surface for all the flow variables equaled to zero.

Wall boundary condition

All the solid surfaces at computational area like buildings, structures and pipes are defined with Wall boundary condition. This condition defines the fact that the gradient for the speed perpendicular to these surfaces is equal to zero, or flow tangents to surfaces.

The regulations on how the convergence is

In the problems associated to transient flow, the early conditions have to be determined in initial, that is, resolving equations regarding time would be possible only by determining the early condition. This is due to the fact that the variables dependant to time are defined using the first derivative test. The early condition in the given scenario is the parameters of field before the pollutants started to emit. As a result, the first step is resolving the stationary flow to achieve the early conditions. After the early conditions achieved, the field parameters over the time given specified time steps have to be obtained. Determine time step to achieve more reliable results is of importance. Select big time steps cause the changes in the field not to be achieved well, and not to lead to reliable results. Small time steps cause substantial computational cost comes to realize. The greatest length that a particle has to pass from the center at flow of the input surface to output surface equals to surface diameter like the upward of computational field, that this diameter equals to 1180 meter. Assumed that this particle passes the computational area with wind speed, as a result passing time would be about 120 seconds. Considering time step equals to 0.01 second, meant that in case which particle moves from its position, a photo taken of it for 12000 times, and/or in moving a particle from field the field equations would be solved for 12000 times.

Results

Firstly, how the ammonia emits at area has been proposed in a three-dimensional way; figure 12 indicates it.

As observed, at the early seconds that ammonia with a given flow rate enters to computational area, its emission would goes upward. By the passage of time, the cloud formed moves in direction with wind. The most important point in ammonia dispersion is its three-dimensional behavior. As observed, ammonia expands in line with z up to Rack structures. To understand better how the concentration changes with time is, the flow lines at different time intervals have been proposed. As mentioned, to model sudden explosion of tank, supposed that the whole mass existing in tank removes in a short while. As a result, ammonia with a given flow enters to the area from the tanks surfaces.

This means that ammonia from the surface of a sphere with a given flow and specific speed enters to the area. This causes totally symmetric flow lines emerge at the early times. Such flow lines remove from the tank perpendicular to it. This phenomenon at 2.57 second after explosion can be observed in figure 13. The time takes ammonia enters to area mentioned 15 seconds, and as a result tank acts as a source till the early 15 seconds, yet wind flow causes mass flow enters to the area in direction with wind. At 8.48 seconds after explosion, simultaneously removing ammonia from tank and moving pollutants towards wind are observed. As pollutants move towards wind, A rotating area has been built, and such a rotating area and vortices that can be observed at 14.96 and 30.96 time intervals after the explosions, cause an area with high ammonia concentration emerges at area. This can be observed in figure 12.

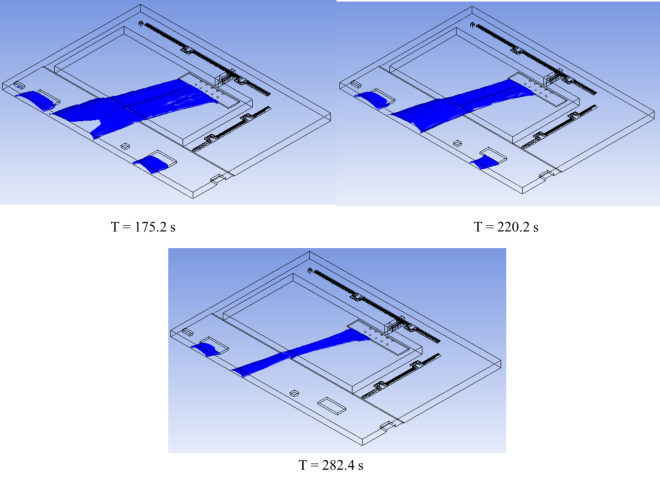Figure 13: fixed concentration surfaces 750 ppm defining ERPG3

Due to this vortex flow, the ammonia existing at this area cannot remove from computational area with wind speed. As a result, one leading factor that causes pollutants concentration at area appears is the existence of vortex flow. The most important limit to develop response program at emergency conditions is the limit in which effects of threatening individuals’ life exist. The most important exposure limits used include:

• Emergency Response Planning Guideline (ERPG) belonged to American Industrial Hygiene Association
• Immediately Dangerous to Life and Health (IDLH)
• Threshold Limit Values (TLV) belonged to American Conference of Governmental Industrial Hygienists

ERPG exposure limit indicates the concentration that causes effects on individuals’ health in compliance with the existing concentrations seen.

ERPG1: This is the maximum airborne concentration below which nearly all individuals could expose to the substance as much as one hour, without any minor and temporary adverse effect on health imposed and smell felt.

ERPG2: This is the maximum airborne concentration below which nearly all individuals could be in this area for an hour using protective instruments or measures.

ERPG3: This is the maximum airborne concentration that causes mortality in exposure with the substance.

Values ERPG1, ERPG2 and ERPG3 for ammonia equal to 25 ppm, 150 ppm and 750 pmm[20]. In figure 14 and 15, fixed concentration levels including 150 ppm and 750 ppm indicating ERPG2 and ERPG3 have been proposed. The first point mentioned before is that pollutants emission at the area is totally a three-dimensional phenomenon, that this indicates the advantage of modeling with CFD. The buildings at computational area include two buildings to control docks located next to dock inside water, as well as 5 buildings in land area .

Figure 14: Flow lines at time intervals 175.2 and 220.2 seconds

 

These sectors include Chlorination unit, control tower, power station, building services, parking lot. Based on EPRG3 exposure limit followed by 30 seconds explosion, the dock control center, control tower building and electricity post are influenced of ammonia pollutant with 750 ppm concentration. followed by 65 seconds after explosion, parking lot and service building are also influenced of this pollutant. Yet with regard to the wind direction, the chlorination area is influence of this pollutant. The results about 2 minutes after explosion have been proposed in this part. In figure 16 and 17, ERPG2 and ERPG3 for different time intervals 175.2, 220.2 and 282.4 followed by emission have been shown. By the passage of time, the limit influenced of emission reduces.

 

As defined, pollutant accumulation at the areas where vortex flow expected can be observed. This is due to rotating and vortex flow. According to figure 17, the most hazardous area in a sudden explosion in tank is the area between service buildings and electricity post. Further, due to rotating flow to 200 seconds followed by emission, ammonia concentration with 750 ppm concentration behind the buildings located in land can be observed. By the passage time and ammonia remove from the computational area modeled in this study, ammonia enters to the petrochemicals upward the dock.

 

Due to wind flow direction, two petrochemicals would be influenced of ammonia dispersion. Further, the fixed concentration levels at 282.4 second followed by emission have not been proposed in figure 17. The reason for this lies in removing pollutant from computational area, that a surface with fixed concentration 750 ppm does not exist at this time interval. Finally, flow lines have been proposed at this time interval. As specified, the flow field found stationary after 4 minutes.

Suggestions

According to the results of the research the software such as CFX that computes and models based on CFD method, with inconsiderable error, are appropriate and reliable for modeling of gas polluter diffusion in the atmosphere, therefore the use of these software instead of Gaussian equation based one is highly recommended.

References

1. Alberto, M. and Hill, T. (2008) CFD and Gaussian atmospheric dispersion models: A comparison for leak from carbon dioxide transportation and storage facilities. Atmospheric Environment, 2008.
2. Cormier, B. R., Qi, R., Yun, G., Zhang, Y., & Sam Mannan, M. (2009) Application of computational fluid dynamics for LNG vapor dispersion modeling: a study of key parameters. Journal of Loss Prevention in the Process Industries, 2009.
3. Kashi, E., et al.(2009) Effects of Vertical Temperature Gradient on Heavy Gas Dispersion in Build up Area. Iranian Journal of Chemical Engineering, 2009.
4. Gavelli, F, Bullister, E. and Kytomaa, H. (2008)Application of CFD (Fluent) to LNG spills into geometrically complex environments. Journal of Hazardous Materials, 2008.
5. Gavelli, F., Chernovsky, M. K., Bullister, E., & Kytomaa, H. K. (2010) Modeling of LNG spills into trenches. Journal of Hazardous Materials, 2010.
6. McBride, M. A., Reeves, A. B., Vanderheyden, M. D., Lea, C. J., & Zhou, X.(2001) Use of advanced techniques to model the dispersion of chlorine in complex terrain. Process Safety and Environmental Protection, 2001.
7. Siddiqui, M., Jayanti, S. and Swaminathan, T.(2012) CFD analysis of dense gas dispersion in indoor environment for risk assessment and risk mitigation. Journal of Hazardous Materials, 2012.
8. Sklavounos, S. and Rigas, F.(2004) Validation of turbulence models in heavy gas dispersion over obstacles. Journal of Hazardous Materials, 2004.
9. Tominaga, Y. and Stathopoulos, T. (2013)CFD simulation of near-field pollutant dispersion in the urban environment: A review of current modeling techniques.Atmospheric Environment, 2013.
10. YU Hong-xi, et al., (2008) Numerical simulation of leakage and dispersion of acid gas in gathering pipeline. Journal of China University of Petroleum, 2008.
11. Zhang, C. N., Ning, P., & Ma, C. X.(2009) Numerical simulation of dense gas leakage in plateau city at complex terrain. Journal of Wuhan University of Technology, 2009.