Department of Computer Applications, Maulana Azad National Institute of Technology Bhopal, India-462003

Article Publishing History

Introduction

Machine learning is the process of learning structure from data, there are various machine learning techniques being implemented to learn from the data. Classification is a data mining technique used to predict group membership for data instances from instances described by a set of attributes and a class label data mining remains the hope for revealing patterns that underlie it (Witten et al., 2011; Li et al., 2016 and Kumar et al., 2016).

There are some basic techniques for data mining like classification, clustering, association rule mining (Pizzuti et al., 2003; Marr, 1981; Wong et al., 2008). Various state of the art classification techniques like Naïve Bayes (Becker et al., 2001), LDA (Quinlan, 1993), SVM (Cortes et al., 1995; Burges et al., 1998; Han et al. 2012; Cunningham et al. 2007), KNN (Han et al. 2012) and Decision Table (DT) has been used for analysis of data.

Figure 1

Figure 2

Figure 3

Figure 4

Figure 5

Figure 6

Figure 7

Figure 8

Figure 9

Figure 10

This paper focuses on the study of the SAGE data of human brain tissues, which is based on the gene expression techniques for analysis of genes. SAGE data sets were collected from SAGE libraries from http://www.ncbi.nlm.nih.gov/projects/SAGEThe classification data were classified into one of the predefined classes and hence from the machine learning perspective it is a supervised learning technique. The Gene expression data is an example of presenting a large number of features (genes), most of the features are irrelevant to the definition of the problem which consequently could degrade the classification process significantly while performing analysis (Banka et al. 2015). This paper primarily focuses on experimentally evaluating different methods for classifying cancerous and non- cancerous tissues.

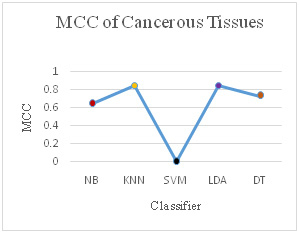Figure 11

Figure 12

Figure 13

Figure 14

Figure 15

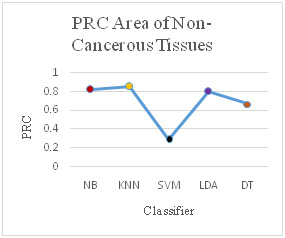Figure 16

Dataset Preparation

Dataset contains 10 Cancerous and 4 normal libraries, these datasets are represented in the form of Table 1 containing tag and frequency. These libraries in the form Tag, frequency1, frequency2, frequency3, frequency14 were combined.

Table 1: Sample SAGE data output
Tag	CCAAAACCCA	ACAAGATTCC	ACCAATTCTA	GCCCTCTGAA	ACCCTAGGAG
Frequency	27	8	56	90	389

Algorithm For Preprocessing

Step 1: The maximum frequency (maxf) and minimum frequency (minf) of each gene in the normal libraries was calculated.

Step 2: The frequency of each gene was compared in the cancerous libraries with the maximum and the minimum frequency of normal libraries.

Step 3: Let a_ij is the frequency of gene j in library i.

1. If (a_ij > maxf) or (a_ij < minf)
2. Change frequency value to 1
3. And 0 otherwise

Step 4: 1 shows the differently expressed genes in the tumor tissue and 0 means no change in the expression level.

Step 5: Records corresponds to ambiguous tags (genes which show over expression in some cancer tissues and under expression in some other cancer tissues) are removed.

The above steps were used for preprocessing on dataset matrix (14×65454) and have been reduced into matrix size (14×1898).

Results And Discussion

The comparison was conducted using the WEKA (The Waikato Environment for Knowledge Analysis) open source software which consists of a collection of machine learning algorithms for data mining. Different classifiers used for evaluation of the cancerous and non- cancerous tissues are discussed below in Table 2. The Performance of the Classifier is discussed in Table 3.

Table 2: Classifiers and their principle
S. No	Name of Classifier	Year	Principle of Classifier
1	Naive Bayes	Classifiers are in use since 1950	Bayesian theorem, it is used when the data is high dimensional.
2	KNN	M. Cover and P. E. Hart in 1967	Closest neighbor whose class is already known.
3	SVM	SVM was introduced by Vapnik in 1995 (Wong et al., 2008).	SVM is based on statistical learning theory and structural risk minimization principal with the aim of determining location of decision boundaries also known as hyperplane.
4	LDA	LDA was introduced by Fishers in 1936.	Compute the d-dimensional mean vectors for the different classes from the dataset, calculate the scatter matrices. Calculate the eigenvectors (e1, e2,…,ed) and corresponding eigenvalues (ë1,ë2,…,ëd) for the scatter matrices. Sort the eigenvectors by decreasing eigenvalues and choose k eigenvectors with the largest eigenvalues to form a d×k dimensional matrix W (where every column represents an eigenvector). Use this d×k eigenvector matrix to transform the samples onto the new subspace. This can be summarized by the matrix multiplication: Y=X×W.
5	DT	Decision tables were introduced during 1960-70.	one of the earliest classification models to be represented graphically because of their easy to understand structure (Quinlan, 1993). It is rule based classifier, where Table represents complete set of conditional expressions, expressions are mutually exclusive in in a predefined area.

It has been observed that the different classification measures have been calculated and compared for cancerous and non-cancerous tissues of human brain. The measures like True Positive (TP) rate, False Positive (FP) rate, Precision, Recall, F-Measure, Mathews Correlation Coefficient (MCC), Receiver Operating Characteristic (ROC) Area and Precision Recall Curve (PRC) Area have been used. The all classifiers have performed well after reducing the number of genes from 65454 to 1898 and the analysis is performed on the 1898 genes which is a significant improvement in reducing the number of features but, it can be revealed from the results that the K-Nearest Neighbor (KNN) and Linear Discriminant Analyzer (LDA) have outperformed the other classifies in most of the performance measures.

Discriminant analyzer technique by (Li et al. 2016) has been proposed to enhance the classification accuracy. Nearest neighbor classifier requires large memory and time (Kumar et al. 2016) but, with our algorithm for preprocessing the dataset has significantly reduced for analysis purpose. A variant of LDA is introduced by (Bacchus et al. 2013) where LDA has performed better than SVM and KNN.

With the help of preprocessing algorithm, we have achieved very good results for SAGE dataset as show in Table 3. The error measures in Figure 17, Figure 18, Figure 19 and Figure 20 Show the different error measure Mean Absolute Error (MAE), Root Means Square Error (RMSE), Relative Absolute Error (RAE) and Root Relative Square Error (RRSE). These measures also show that LDA and KNN have performed very well and the error are less in comparison to other classifiers used.

Table 3: Classifiers and their performances
S. No	Name of Classifier	Performance of Classifier
1.	Naive Bayes	For our dataset it has Correctly Classified 12 instances that is the 85.7143 % and 2 instance are incorrectly classified which is 14.2857 %
2.	KNN	For our dataset it has correctly classified instances are 13 which is 92.8571 % and the incorrectly classified instances 1 that is 7.1429 %
3.	SVM	SVM classified correctly 10 instance which is 71.4286 % of the total and the remaining 28.5714 % are incorrectly Classified Instances.
4.	LDA	Correctly classified instances are13 which is 92.8571 % and incorrectly classified instance is 1 that is 7.1429 %. By LDA.
5	DT	In our experiment 12 instances are correctly classified which is 85.7143 % and 2 instances are incorrectly classified which accounts for 14.2857 % by DT.

Figure 17

Figure 18

Figure 19

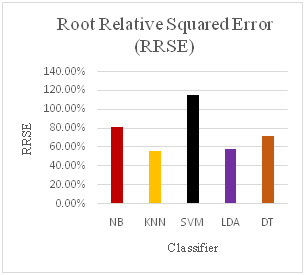Figure 20

Comparison of Different Performance measures for Tumorous Tissues and Non-Tumorous Brain Tissues

Error Measures for various Classifiers

Conclusion

SAGE data has been preprocessed and thereby reducing the number of features to 1898, samples are classified and their performance is compared. The classifiers employed here have used statistical approaches and focused on individual features. Future work can be enhanced to the study of features in the groups. Implementing the association rule mining techniques along with soft fuzzy techniques can be of great significance for the reduction in the number of features and performance enhancement can be achieved.

Acknowledgement

This work was supported by research grant from MANIT, Bhopal, India under Grants in Aid Scheme 2010-11, No. Dean (R&C)/2010/63 dated 31/08/2010.

References

Bacchus A, Biet M, Macaire L, Menach Y L and Tounzi A (2013). Comparison of Supervised Classification Algorithms Combined with Feature Extraction and Selection: Application to a Turbo-generator Rotor Fault Detection, 9th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives (SDEMPED). 558-565.

Banka H, Dara S (2015). A Hamming distance based binary particle swarm optimization (HDBPSO) algorithm for high dimensional feature selection, classification and validation. Pattern Recognition Letters. Vol 52, 94–100.

Becker B, Kohavi R, Sommerfield D (2001). Visualizing the simple Baysian classifier, in: Information Visualization in Data Mining and Knowledge Discovery. Inc. San Francisco, CA, USA, Morgan Kaufmann Publishers. 237-249.

Burges C. J.C. (1998). A Tutorial on Support Vector Machines for Pattern Recognition. Data Mining and Knowledge Discovery 2, 121-167.

Cortes C, Vapnik V (1995). Support vector networks. Machine Learning, Boston, Kluwer Academic Publishers. Vol 20, 273–297.

Cunningham P, Delany S. J (2007) k-Nearest Neighbour Classifiers Technical Report UCD-CSI.

Han J, Kamber M (2012). Data Mining Concepts and Techniques. Elsevier.

Kumar R.R, Viswanath P, Bindu C.S (2016). Nearest Neighbor Classifiers: Reducing the Computational Demands, 6th IEEE International Conference on Advanced Computing. 45-50.

Li L, Du L, Zhang W, Hen H, Wang P (2016). Enhancing information discriminant analysis: Feature extraction with linear statistical model and information-theoretic criteria, Pattern Recognition Vol. 60,554–570.

Marr J.D (1981). Comparison of several clustering algorithms for data rate compression of LPC parameters. IEEE International Conference on Acoustics, Speech, and Signal Processing ICASSP’81. Vol 6, 964-966.

Pizzuti C, Talia D (2003). P-AutoClass: scalable parallel clustering for mining large data sets IEEE Transactions on Knowledge and Data Engineering. Vol 15, Issue 03, 629-641.

Quinlan J.R (1993). C4.5: Programs For Machine Learning, Morgan Kaufmann Publishers, Inc.

Witten I.H, Frank E, Hall M.A (2011). Data mining practical machine learning tools and techniques, Morgan Kaufmann publisher, Burlington.

Wong A.K.C, Li G.C.L (2008). Simultaneous pattern and data clustering for pattern cluster analysis. IEEE Transactions on Knowledge and Data Engineering. Vol 20, Issue 07, 911-923.