Ghaida Almanea, Rajwah Alqurashi, Nouf Alharbi, Reem Alharkan, Fahdah Alsadhan Software Engineering
Department,College of Computer and information Sciences, King Saud University Riyadh, Saudi Arabia

Corresponding author email: Ghaaida19@hotmail.com

Article Publishing History

INTRODUCTION

Assigning groups of students to a limited number of projects while satisfying the capacity constraints is a significant chore at the most educational establishments.The group of students must enter score of their project preferences, in matrix of project-students matrix. The problem of project-students allocation is becoming more complex and harder when the number of projects and groups becomes bigger (Budish, & Cantillon,2012).The project conflicts are another issue need to resolved   which make the problem of project-students allocation more harder (Arulselvan et. al,  2016).

The Graduation Project Committee (GPC) at the Software Engineering Department in King Saud University (SWE-KSU) solve project-students problem every semester. Relegating groups of students to an arrangement of graduation ventures while fulfilling the capacity and GPA criteria for each group. At the moment, the project allocation process is done manually at SWE-KSU by having groups select their list of preferred projects, then having GPC members filter the wishes based on GPA, while making sure the project matches the group’s capacity. This process is time and effort consuming, especially when dealing with many projects.

To deal with this issue, the automated group-project allocation solver is proposed in this paper to tackle this problem by satisfying all the constraints. The project-allocation process includes having each group select a list of projects depending on their inclinations and preferences, ordered from the most preferred project to the least preferred project. The group with a higher GPA will be assigned the first choice, if it fulfils capacity constraints. The group-project allocation solver (a greedy linear heuristic) aims to automate the process while satisfying the hard limitations (capacity), GPA, along with the soft limitations (projects preference inclinations).

Related Work: There is a growing need to automatically assign project to students due to the increasing number of students. In the scientific literature, various studies are presented to dealing with the project – students allocation problems. An incredibly old initial study for allocating projects to students is proposed in the 1970s (Proll, 1972). The proposed algorithm was based on a simple objective method for assigning projects to students with consideration of student preferences. A linear-time algorithm is proposed in (Abraham et. al, 2003) to address the student-project allocation problem. The proposed algorithm attempts to find an optimal stable matching with respect to the students’ aspects. Kwanashie et. al (2015) proposed an effective method to obtain the a greedy maximum matching assignments based on lexicographically maximum concept. The proposed algorithm  is able to find the lexicographically maximum in assignments network.

A recent student-project allocation study has been presented  by Chiarandini et. al, (2019) where  a mixed integer linear programming problem is formalized to handle the first-year course at the Faculty of Science of the University of Southern Denmark as  a case study. The problem is modeled based on model fairness and utilitarian principles. Different state-of-the-art commercial solvers is compared with respect to computational effort and the quality of the allocations solutions by means of a state-of-the-art commercial solver.

The main findings of these models have  significant effects on the student assignments distribution. In  the Olaosebikan, and Manlove, (2018)  model, a student-project allocation problem SPA with lecturer preferences over Students with Ties (SPA-ST) was investigated. The study aimed to find an optimal matching where allocating students over projects based on preferences of student over project. In the work of Abraham et al, (2006), two algorithms were proposed to solve the student-project allocation problem. First algorithm produced best-possible stable matching for students while the second algorithm produced best-possible stable matching for the supervisors. A two sided-based model for the Student-Project Allocation problem was proposed by Manlove & O’Malley, (2008). In this model allocation problems were solved when both students and advisors have preferences over projects.

The main finding of study was that maximum stable matching problem is NP-hard. In (Wilson, 1997) a genetic algorithm with an adapted fitness function  was employed to address project assignment problems. The proposed GA based method used dataset of University of Southampton. The experimental result shows acceptable solution could be obtained.  Another study (Harper et. al,2005)  applied a genetic algorithm to solve the project-students assignment problem. The comparison reveals that the GA based model is superior to the optimal integer programming model and it was able produced a better assignments solution.  Many automated matching systems based on efficient algorithms is developed and widely used in various universities such as the University of Southampton (Harper et. al, 2005,  Anwar & Bahaj,2003) and University of York (Kazakov, 2002). In (Lightfoot, 2016) an automate system for the assignment of students to projects is developed to find the optimal student-project matching. This system designed to solve the problem of assigning students to projects with consideration only for student preference and capacity as constraints.

None of the previous studies have been addressed  student-project allocation problem as we  have described in this paper. They had  tackled   their own student-projects allocations, considering their own criteria. In this paper, we  have  addressed student-project allocation problems at the Software Engineering Department in King Saud University (SWE-KSU) using a new  linear heuristic algorithm that designed to meet the GPC requirements at SWE department. This  study is a part of the development of  an automate system to  be used by the Graduation Project Committee (GPC) at SWE-KSU.

Research Methodology: The project-student assignment problem is a special case of the generalized assignment problem (Harper, et. al,2005, Biró et al 2010). An instance of the project-student assignment problem comprises of a set of project, students, and advisors. Each project should be supervised by only one advisor. The group of project has capacity constraint. Each group of students have preferences over projects. While the advisors have no preferences over the students. The group of students with the higher GPA average is more likely to match with their first preferences. An instance of the project-student assignment problem  can be defined as follows:  let P = {p1, p2, p3} be a set of projects with its own student capacities, and let G = {G1, G2, G3} be a set of groups. And let AC= {AC1, AC2, AC3} be the set of acceptable project allocation for each group based on capacity (feasible solution). Finally, let AG be the set of ordered groups with the highest GPAs.

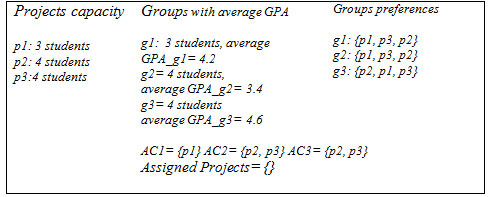
An example the project-student instance is shown in Figure 1. In this example, we have a project capacity of p1 of 3 students, p2 of 4 students and p3 of 4 students. Groups with average GPA as follows: Group 1of 3 students, Group 2 of 4 students and Group 3 of 4 students are having average GPA equal to 4.2, 3.4 and 4.6 respectively. So, the groups preferences are ordering as follows: G1: {p1, p3, p}, G2: {p1, p3, p2} and G3: {p2, p1, p3}. Based on capacity: the acceptable allocation sets for G1 = AC1 , for G2 = AC2 and for G3 = AC3. Thus, AC1= {p1} AC2= {p2, p3} AC3= {p2, p3} with Assigned Projects= {}. Based on GPA: Set of ordered groups with highest GPAs= AG to be: AG= {G3, G1, G2}, start with G3,  AG ∩ G3 select first choice = p2 ,  AG ∩ G1 select first choice = p1, AG ∩ G2 select first choice = p3.

Figure 1: An instance of the project-student allocation problem

In this section, we propose a greedy linear heuristic algorithm namely (GLHA) to address the project-student allocation problem that described above. The proposed algorithm finding a student-project optimal stable matching in a sequential liner manner by evaluating project preferences of each  group in order to satisfying all the hard constraints (capacity) and the soft constraints (groups’preferences) as much as possible based on the GPA criteria. GLHA assigning groups of students over a set of projects through sorting the groups in a descending order based on the average GPA and the project preference of each group is sorted ascending based on the highest weights. To assign a project to a group, the capacity of the project must match the capacity of the group and the project must be available (feasible). The pseudocode of greedy linear heuristic algorithm (GLHA) is shown in Algorithm1.Initially all group of students in G are unassigned to any project p.

Each project  has own limited capacity of student.  The proposed algorithm begins with sorting the groups ascending based on the average GPA (stept2), then for each group sorting the projects ascending based on the highest group’s preference (step3). The group select the project that have the same group capacity, then assign the groups to the selected project and set the project status as “Taken” and removed from the project set (step9) This process is repeated in step 4 through step 12.  The special case for greedy heuristic algorithm is when the two groups have the same GPA and they both select same project; the algorithm will assign the group to the project randomly. The GLHA terminates when all the projects are assigned to groups i.e. the  =Ø.

RESULTS AND DISCUSSION

In this work, we used graduation projects for bachelor’s degree at KSU-SWE in the two academic semesters Spring/Fall 2018 as a case study. We applied our proposed greedy linear heuristic algorithm (GLHA) on different KSU-SWE Spring/Fall 2018 real-datasets.  The spring semester 2018 dataset, as shown in Table 1, is quite small. It consists only 4 projects and 4 groups with total of students equals to 17. However, the distribution of students among the group is vary between 4-5 students, which make the allocation problems more complex.  The fall semester 2018 dataset, as shown in Table 2, it bigger than spring dataset. It consists 13 projects with varied capacities and 13 groups with total of students equals to 65. Despite of the big of dataset, students are distributed among the group are uniformly which make the allocation problems much easier.  We ran GLHA algorithm 10 times for each dataset on Intel(R) Core (TM) and implemented using C# Visual Studio enterprise 2017.

For each run, the group’s preferences are randomly generated GLHA was able to compute the allocation up to 13 project/group with varied capacities and distribution. Tables 3 and 4 show the results of 10 runs in spring and fall 2018, respectively. For Dataset of spring 2018, the worst obtained solution is the first run as the data set violates the hard constraint (capacity) while  the best optimal solution is obtained in  seventh   run as the dataset as it satisfies the capacity constraint with the less time.  For Fall 2018 dataset,  the worst obtained solution is the first run where violation of the hard constraint (capacity) is occurs, the best optimal solution is obtained in  tenth  run as it satisfies the capacity constraint with the less time and it satisfies the soft constraint of groups’ preferences.

Table 1. KSU-SWE dataset of Spring 2018

groups#	Student Number	GPA Average		Group Preferences		Project #	Project Capacity	Manual Assignments
G1	4	4.50		P2, P3, P1, P4		P1	4,5	G1->P2
G2	4	4.24		P2, P1, P3, P4		P2	3,4	G2->P4
G3	4	4.65		P3, P4, P2, P3		P3	5	G3->P3
G4	5	4.39		P2, P1, P3, P4		P4	4	G4->P1
Total number of groups:			5
Total number of projects:			5
Total number of students: Assignments Time:			17 ≈15 (mins)

Table 2. KSU-SWE dataset of Fall 2018

groups#	Student Number	GPA Average	Group Preferences				Project #	Project Capacity	Manual Assignments
G1	5	4.10	P2, P1, P11, P3,P5, P4, P9, P12, P8,P7,P6,P13,P10				P1	4,5	G1->P11
G2	5	3.99	P2, P1, P3, P8,P9, P4, P5, P6, P7,P11,P12,P13,P10				P2	3-5	G2->P9
G3	5	4.23	P2, P4, P5, P6,P3, P1, P11, P13, P12,P7,P8,P9,P10				P3	5	G3->P4
G4	5	3.50	P3, P2, P4, P1,P7, P6, P11, P12, P10,P8,P5,P9,P13				P4	4	G4->P10
G5	5	4.50	P3, P2, P1, P7,P8, P9, P5, P6, P4,P10,P12,P11,P13				P5	4,5	G5->P7
G6	5	4.89	P2, P3, P4, P1,P6, P5, P7, P8, P10,P12,P9,P13,P11				P6	4,5	G6->P2
G7	5	4.71	P2, P1, P4, P3,P7, P12, P6, P10, P8,P5,P11,P9,P13				P7	4,5	G7->P1
G8	5	4.20	P2, P7, P1, P3,P4, P12, P13, P11, P6,P9,P5,P8,P10				P8	4,5	G8->P12
G9	5	4.42	P2, P8, P6, P5,P9, P7, P4, P1, P3,P12,P11,P13,P10				P9	4,5	G9->P1
G10	5	4.03	P3, P1, P4, P5,P6, P12, P2, P10, P8,P13,P7,P9,P11				P10	4	G10->P6
G11	5	4.66	P5, P1, P2, P3,P4, P7, P8, P12, P6,P10,P11,P13,P9				P11	5	G11->P5
G12	5	4.58	P1, P3, P2, P4,P10, P6, P7, P5, P10,P13,P11,P9,P8				P12	5	G12->P3
G13	5	3.2	P4, P3, P2, P1,P8, P7, P6, P12, P5,P9,P10,P11,P13				P13	5	G13->P13
Total number of groups:				13
Total number of projects:				13
Total number of students: Assignments Time:				65 ≈65 (mins)

Table 3. Experimental results on Spring 2018 KSU-SWE dataset

Run	#Groups/Projects	Use of Capacity	Violates Capacity Hard Constraint	Violates Group/s Preference Soft Constraint	Time (sec.)
1	4	Yes	Yes	Yes	1.55
2	4	No	No	Yes	1.37
3	4	Yes	No	No	1.15
4	4	Yes	No	No	1.18
5	4	Yes	No	No	0.58
6	4	Yes	No	Yes	1.45
7	3	No	No	Yes	0.43
8	3	Yes	No	No	0.59
9	3	Yes	No	No	0.55
10	3	Yes	No	No	0.54
Best	7	–	–	–	0.43
Worst	1	–	–	–	1.55

Table 4. Experimental results on fall 2018 KSU-SWE dataset

Run	#groups/projects	Use of capacity	Violates Capacity Hard Constraint	Violates Group/s Preference Soft Constraint	Time (sec.)
1	13	No	No	Yes	2.75
2	13	Yes	Yes	Yes	2.35
3	13	Yes	No	No	2.27
4	13	Yes	No	No	2.20
5	12	No	No	No	1.27
6	11	Yes	No	No	1.45
7	12	Yes	No	No	2.43
8	10	Yes	No	No	1.75
9	11	Yes	No	No	2.36
10	9	Yes	No	No	1.25
Best	10	–	–		1.25
Worst	2	–	–		2.35

Based on the experimental   results that shown in tables 2 and 3. We can demonstrate that GLHA has a capability to finds a stable matching of groups to projects when applied to solve the project-group allocation problem at KSU-SWE.  GLHA can assigned up to 13 project/group with varied capacities and students’ distribution in the most cases with no violation of hard nor soft constraints.  the capacity and groups preferences constraints in a reasonable time comparing to the manual assignments.  Our proposed algorithm is satisfied both capacity and group’s preference constraints.   For spring 2018 dataset, the algorithm could meet the group’s preference constraints and find the optimal matching in seven out of ten cases. While the algorithm could meet the soft constraints and find the optimal matching in the nine out of ten cases for spring 2018 dataset. It is interesting the GLHA perform slightly better in the fall 2018 dataset than the spring 2018 dataset.

This can be indicating that the GLHA can be more efficient when solving a dataset with bigger size. The distribution of student over the groups can be an effective factor. As students are distributed uniformly in the fall 2018 dataset which might affect the performance of the GLHA positively. It is It is known that the number of students in the groups are strongly related the project capacity (soft constraint).  This is so clear in the result of the spring 2018 dataset. The violation that occurs in some case belongs to the variance of the student’s distribution and projects capacities.   No existing studies are addressed same SWE_KSU student-project allocation problem with same constraints and criteria.

However, Our proposed  GLHA could be comparative to the method presented in  (Chiarandini et. al, 2019) that addressed student-project allocation problem for   the Faculty of Science of the University of Southern Denmark in team of the performance and speed.  Our method are able to perform the allocation process in the responsible time with good quality solution). However We believe that the complexity of the dataset might be challenging to the GLHA in some cases. we strive to increase the generality of the algorithm to address different type of the project-group allocation problem in the future. Also, more enhancements will be added to the greedy linear heuristic algorithm to increase its efficiency.

CONCLUSION AND FUTURE WORK

In this paper, a greedy linear heuristic algorithm (GLHA) is presented to solve group-project allocation problem, by satisfying all the hard constraint (capacity) and the soft constraints (groups’ preferences) as much as possible based on the GPA criteria. The aim of our proposed heuristic is to produce a good quality solution in a reasonable time. Moreover, the paper presents the project-group allocation problem at SWE-KSU using a greedy linear heuristic algorithm. The proposed algorithm is specifically designed to meet the GPC requirements at Software Engineering department at KSU. However, we strive to increase the generality of the algorithm to address different type of the project-group allocation problem in the future. Also, more enhancements will be added to the greedy linear heuristic algorithm to increase its efficiency.

ACKNOWLEDGMENTS

The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding this work through the Undergraduate Research Support Program, Project no. (URSP – 3 –18 – 145).

REFERENCES

Abraham D.J. , Irving R.W., and Manlove D.F. (2003). The Student-Project Allocation Problem. In Proceedings of ISAAC 2003: the 14th Annual International Symposium on Algorithms and Computation, volume 2906 of Lecture Notes in Computer Science, 474-484. Springer-Verlag.

Abraham D.J. , Irving R.W., and Manlove D.F. (2007) Two algorithms for the Student-Project Allocation problem Journal of Discrete Algorithms 5 (1), 73-90

Anwar A.A. and. Bahaj. A.S (2003) Student project allocations using integer programming.

IEEE Transactions on Education, 46(3), 359-367.

Arulselvan, A., Cseh, Á., Groß, M., Manlove, D.F., and  Matuschke, J. (2016). Matchings with lower quotas: Algorithms and complexity. CoRR arXiv:1412.0325. Preliminary version appeared at ISAAC 2015.

Biró, P., Fleiner, T., Irving, R. W., & Manlove, D. F. (2010). The college admissions problem with lower and common quotas. Theoretical Computer Science, 411(34), 3136–3153. https://doi.org/10.1016/j.tcs.2010.05.005.

Budish, E., and Cantillon, E. (2012). The multi-unit assignment problem: Theory and evidence from course allocation at Harvard. American Economic Review, 102(5), 2237–71. https://doi.org/10.1257/aer.102.5.2237.

Chiarandini, M., Fagerberg, R. and Gualandi, S. (2019).  Handling preferences in student-project allocation. Annual Operational Research 275, 39–78 (2019). https://doi.org/10.1007/s10479-017-2710.

Harper PR., Senna V, Vieira I and Shahani. AK.  (2005) A genetic algorithm for the project assignment problem, Computers & Operations Research, 32, 1255–1265.

Kazakov D. (2002) Co-ordination of student-project allocation. Manuscript, University of York, Department of Computer Science.

Kwanashie A., Irving R.W., Manlove D.F., Sng C.T.S. (2015) Profile-Based Optimal Matchings in the Student/Project Allocation Problem. In: Jan K., Miller M., Froncek D. (eds) Combinatorial Algorithms. IWOCA 2014. Lecture Notes in Computer Science, vol 8986. Springer, Cham

Lightfoot S., (2016) Solving the student project allocation problem, Master Dissertation Department of Computer Science, University of Manchester.

Manlove D.F.  and O’Malley G. (2008) Student-project allocation with preferences over projects. Journal of Discrete Algorithms, 6 (4), 553-560.

Olaosebikan, S. and Manlove, D.  (2018) Student-Project Allocation Problem with Ties, Conference: Scottish Informatics & Computer Science Alliance (SICSA PhD Conference 2018) DOI: 10.13140/RG.2.2.14079.25765

Proll. L.G. (1972) A simple method of assigning projects to students. Operational Research Quarterly, 23(2):195-201.

Wilson JM (1997). A genetic algorithm for the generalized assignment problem. Journal of the Operational Research Society, 48, 804–9.