Educational Psychology Department, Faculty of Education, Suez Canal University, Ismailia (41522), Egypt,

Corresponding author email: mahmoud_muhanna@edu.suez.edu.eg

Article Publishing History

INTRODUCTION

Statistics courses are prescribed by the Department of Educational Psychology in the colleges of education in the Arab Republic of Egypt. They are derived from the branch of Pure Mathematics.  These courses serve the field of education by converting psychological phenomena into figures describing such psychological phenomena and determine their existence as predictors of decision-making in terms of modifying psychological, personal and cognitive phenomena.Psychological statistics is a course based on the combination of mathematical problems requiring deductive calculations and verbal issues requiring the learner’s mastery of logical thinking, abstraction and representation skills (Hsin & Paas, 2015). The psycho – deductive statistical course is a course based on the linkage between meaningful real-life problems that require meta-cognitive skills and mathematical thinking skills to analyze and study given tasks (Leahy & Sweller, 2019). Redifer, Bae & DeBusk-Lane (2019) noted the cognitive load in essence is a mental effort that refers to the cognitive sources needed to perform certain tasks.

Sweller founded the theory of cognitive load as he criticizes the traditional methods of solving mathematical problems, because they load working memory with new cognitive processes, and thus do not transfer new information to long-term memory (Leahy & Sweller, 2019). He tried to study other possibilities to embody problems related to practical examples and open tasks so that processing processes improve better during Problem Solving to reach the Psychological statistics is a course based on the combination of mathematical problems requiring deductive calculations and verbal issues requiring the learner’s mastery of logical thinking, abstraction and representation skills (Hsin & Paas, 2015).

The psycho – deductive statistical course is a course based on the linkage between meaningful real-life problems that require beyond-knowledge skills and mathematical thinking skills to analyze and study given tasks (Leahy & Sweller, 2019). Redifer, Bae & DeBusk-Lane (2019) noted the cognitive load in essence is a mental effort that refers to the cognitive sources needed to perform certain tasks. Sweller founded the theory of cognitive load as he criticizes the traditional methods of solving mathematical problems as they exhaust working memory with new cognitive processes, and thus do not transfer new information to long-term memory (Leahy & Sweller, 2019). He tried to study other possibilities to embody problems related to practical examples and open tasks so that treatment processes improve better during Problem Solving to attain the target goals. instead of routinely transferring knowledge and classifying it into routine patterns of solution ideas. Accordingly, this study attempted to pose mathematical problems via the psychological statistics decision based on open tasks establishing new ideas instead of traditional mathematical problems with familiar images as reported by Treffers (2019).

The current study proposes mathematical problems via the psycho-deductive statistical course that provides open tasks allowing the learner to employ new ideas rather than relying on familiar images of traditional mathematical problems (Treffers, 2019). Open tasks in mathematics aim to incorporate cognitive, linguistic, social, and emotional processes into problem-solving processes (Fuchs, Fuchs, Malone, Seethaler & Craddock, 2019). The inclusion of those processes is limited by the ability of the working memory and is influenced by many other characteristics of the learners and current knowledge, as well as the nature of the new information available during the tasks analyzed by learners. Thus, learners with effective working memory undergo  a less cognitive load (Redifer et al., 2019).

The Cognitive Load Theory: The cognitive load theory is an educational theory based on human knowledge structure. Mathematical problem-solving are a complex cognitive and perceptual task that imposes a large disruption on working memory. It involves combination problems of words, mental schemas, and information not related to the problem and the selection of the most suitable solving strategies and applying mathematical processes principles to expose the required response (Fuchs et al., 2019; Hsin & Paas, 2015).  These principles as the following (Chen, Castro-Alonso, Paas & Sweller, 2017; Leahy & Sweller, 2016; Sweller, 2011):Mathematical operations and problem solving are complex cognitive and cognitive tasks that impose a significant cognitive load on the working memory as they involve problems combining words, mental representations, information unrelated to the assigned problems, selecting the most appropriate strategies for the solutions and applying the principles of mathematical operations to reach the desired response (Fuchs et al., 2019; Hsin & Paas, 2015). They can be summarized in the following principles (Chen, Castro-Alonso, Paas & Sweller, 2017; Leahy & Sweller, 2016; Sweller, 2011):

1. Long-term memory is a storehouse for keeping information, wherein one keeps a huge amount of information stored in their long-term memory.
2. Integration of Schema Theory with the principle of recall and reorganization. Most information is stored in long-term memory in the form of cognitive charts. Schemes are called upon by imitating, reading, viewing material or listening to others.
3. Problem-solving, and random start-up occurs if information is not available in long-term memory. Problem solving necessitates examining the cognitive schemata and processing information for the current situation sequentially. An example of this happens when a teacher is asked to explain an incomprehensible mathematical issue to a student outside class. Redifer et al. (2019) state that problem solving depends on differences between learners in cognitive ability and the nature of the tasks they perform, and the shortcoming increases as the complexity of the content of those tasks is enhanced.
4. Working memory and its limited capacity for change. The process of organizing and generating the cognitive structure requires the ability to produce unlimited sets of new information while excluding unnecessary information that prevents working memory from processing the information as a limited processing source in terms of capacity and time.
5. Long-term working memory and the principle of interconnection and environmental organization to form the cognitive structure of the information being processed. In the light of this principle, it is possible to transfer unlimited amounts of information from long-term memory to working memory so as to generate new procedures suitable for accommodation with the environment and then built out a sequential organization in the form of cognitive and, personal and social schema.

According to these principles, the main goal of learning is to create cognitive schemes, process them in the working memory and then keep them in long term memory. Learning becomes effective if schemes fail to disrupt the information structures previously stored in long-term memory (Leahy & Sweller, 2016, 2019). Thinking processes require cognitive structures formation based on the datum of the presented statistical problems. This information requires secondary information that demands recall data from long-term memory and should be organized to benefit from the instructions available in the statistical problem and help the learner acquire new knowledge (Chen et al., 2017). Datum analysis requires a series of interactions of separate elements that must be processed simultaneously in the working memory (Leahy & Sweller, 2019; Sweller, 2015).  Thinking processes entail the formation of cognitive structures from the initial information (data) of the statistical problems at hand and this information entails secondary information recalled from long-term memory and organized to take advantage of the instructions available in the statistical problem to help one acquire new knowledge (Chen et al., 2017).

Data analysis requires a chain reaction of discrete elements to be processed simultaneously in the working memory (Leahy & Sweller, 2019; Sweller, 2015). The interaction of the element varies due to the internal cognitive load by changing what to learn or by changing the experience of the learners. Once learning occurs, information is encoded and stored as interactive elements (cognitive schema) in long-term memory (Leahy & Sweller, 2019; Sweller, Kirschner & Clark, 2007).The knowledge of working memory is addressed by adopting the principle of organization and environmental connectivity as one element so as not to exhaust the working memory.

For example, a statistical problem can be read easily and quickly to find out its variables and methods of solution already written in long-term memory. Information and equations are retrieved to the working memory as solution equations whose variables are changed according to the nature of the mathematical problem. Thus, the interaction of information is automated, i.e. thinking becomes stereotyped. If mathematical problems are open-ended, i.e., when the learner himself raises research questions in the light of the piece of reading that presents the statistical problem, the methods of solution are numerous, the learner is free from stereotypical thinking and the cases of internal and external load are reduced, and the predominant load in this case is the extraneous load (Tricot & Sweller, 2014).

The cognitive load is concerned with producing educational techniques that rely on the efficiency of limited information processing ability of learners to apply the knowledge and skills acquired in new situations. Cognitive load depends on the cognitive structure treated in the working memory as partially independent processing units for visual and auditory information, which interacts with unlimited long-term memory (Paas, Tuovinen, Tabbers & Van Gerven, 2003).

Cognitive load and mathematically complex tasks: The cognitive load refers to the mental effort or cognitive resources needed to perform mathematics tasks. Tasks’ nature imposes the working memory load during learning processes. The higher the mental effort on complex tasks, reducing the learner’s performance on these mathematical tasks (Orru & Longo, 2018; Peck, Doan, Bourne & Good, 2018).Whenever the mathematical problem requires an innovative intellectual product, this internal cognitive load depends on the successive mathematical task difficulty. The external cognitive load may be related to the learner or the task to be accomplished.Given that creative thinking requires some characteristics of complex cognitive tasks it is expected that a more complex implicit nature enhances the cognitive structure efficiency, which has negative influences on those with stereotypical thinking in statistical problem-solving (Redifer, Bae & DeBusk-Lane, 2019; Seufert, 2018).

Complex tasks require intervention during problem-solving to develop evaluations, especially in multi-step problems, which increases the learner’s personal experience in dealing with similar tasks in content a different context later (Chen, Retnowati & Kalyuga, 2019). Training on mathematical and statistical problem solving reduces stereotypical thinking and improves monitoring accuracy and individual judgment with increasing age (Baars, Van Gog, de Bruin & Paas, 2017).

Factors affecting cognitive load

Task switching: Most math-related problems can be classified as variable problems consisting of an initial state and a goal to solve problems in a simple manner. These problems can be solved using the means-ends analysis method which involves trying to minimize differences between problem elements, identifying solution sub-strings deducing what is required to prove and then building the proof in the commonly accepted ways. The learner then proceeds to analyze new sub-elements, which are not included in his statistical cognitive charts, on his mind, (Sweller, 1988). Analyzing the problem into its sub-elements also decreases the mental effort involved in solving problems.

The time needed to process a task in the working memory: The learner’s ability to control attention helps to predict a successful solution to problems that require certain stages of conclusion and reconstruction of the cognitive structure to reach the goal of problem-solving (Goel & Schnusenberg, 2019; Wieth & Burns, 2014).

Common errors: Common errors result from random retrieval of information and subsequent failure to read and process all elements of statistical issues in light of insufficient time for the central port to work in synergy with the visual component. Common errors usually range from 35% to 37% in the resolutions of issues with similarities between elements of prior cognitive schemes (Schaper & Grundgeiger, 2019). In addition, common errors may occur as a result of the learner’s cognitive beliefs, which relate to the nature of knowledge use and become inputs to the metacognitive processes. Implicit beliefs influence higher problem-solving skills such as effective observation of understanding, application of strategies, and perseverance (Redifer et al., 2019).

Dynamic Critiquing: It occurs when a learner departs from the usual framework of thinking, providing proofs or evidences, employing steps to attain a critical solution to a statistical problem without being constrained by the evaluator in a particular way in the solution. The external or intrusive cognitive load occurs as a result of inverse thinking that is supposed to determine the nature of the cognitive scheme and lead the learner to choose the dynamic construction of the solution to frame the cognitive structure of the solution (Sweller, 1988; Wieth & Burns, 2014).

Cognitive Inhibition: Cognitive inhibition refers to the mental effort involved in processing information needed to perform a task that appears to form stereotypes as key considerations for solving statistical problems, constraining the working memory and limiting its paths. If learners encounter a problem that requires creative solutions, this leads to limitations related to factors within and outside the person associated with the tasks that do not compromise with their thinking patterns (Redifer, Bae & DeBusk-Lane, 2019).

Issues with Hybrid text problem methods: Problem solving occurs through three stages: searching for an initial representation of problems, reaching a predicament, restructuring the representation of the problem using alternative methods for a particular stage of mathematical proof formation (Wieth & Burns, 2014). The more creative the learner is in perceiving the relations between data issues, the more he or she becomes able to adopt flexible statistical methods that enable him to formulate the research questions, test the hypotheses leading to marked improvement in the speed of processing information in the working memory. Learner’s assimilation of a large number of ideas   addressed before, is the central controller of information processing that turns deep encryption to automatic encryption during information processing (Goel & Schnusenberg, 2019; Norouzi, Vaezmosavi, Gerber, Pühse & Brand, 2019). In the absence of identical elements in the statistical problem, which the learner solves with the prior knowledge schemes, leads to heterogeneous cognitive processes resulting in a load that reduces the efficiency of the working memory in processing the available information (Neumann & Russell, 2019).

Cognitive load patterns: Cognitive load theory summarizes the structure of information as chains reducing difficulty by focusing cognitive activity on schema acquisition. Cognitive load theory deals with learning difficulties and artificial problem solving where they can be addressed by educational design (Sweller, 1994). This theory includes guidelines for reducing cognitive activity that hinders learning and estimating the multifaceted relationship between learning and assessment. Key issues around cognitive load types include the context wherein learning occurs, the continued use of single-component mental effort assessments, the timing of cognitive load and measurements of learning outcomes. The types of cognitive load can be presented as follows (Leppink, 2017; Orru & Longo, 2018; Sweller, 2011).

1. Internal cognitive load is the difficulty related to the content being processed. It is necessary to realize that the cognitive load that results from the interactive elements of information that need to be addressed simultaneously to achieve the goal of education. It is often concerned with the implicit or explicit meaning of information.
2. External cognitive load refers to the way information is presented to learners under the control of the educational designer. It is produced by the requirements assighned by the teacher to learners, or the instructions that they are asked to follow by integrating a set of information before being able to examine the paths of possible solutions (Chinnappan, 2010). This load increases by enhancing ineffective learning methods that inadvertently distract learners who have distracting information or make a task more complicated than it should be. The internal cognitive load occurs during creative thinking due to the difficulty of the mathematical task itself while the external load can be caused by factors within learners themselves, encouraging them complete the task (Orru & Longo, 2018; Redifer et al., 2019). Practical examples reduce the external load as they are effective ways to teach complex problem-solving skills (Paas & Van Gog, 2006).

The intrusive cognitive is defined by Sweller (2010) as a purely function of the working memory resources allocated to the interaction of specific elements of the internal cognitive load. The load is assumed to enter the learner’s high motivation. The intruder load is also inversely proportional to the external load provided the learner’s cognitive abilities are high. It is produced by building schemes and is considered desirable, helping to learn new skills and other information (Paas & Van Gog, 2006; Seufert, 2018). The scheme is conceived as a notion or a specific object that tells us what to expect when we encounter it in the future.

Sprinkle Sweller (2010) state that the interaction between the elements in this load is associated with characteristics of the learner. A less experienced learner may process a range of information within the working memory, this multi-information is one structure possessed by more experienced learners regardless of the nature of the subject they study. In other words, the intruder load is independent of the information provided. For example, assuming that there is a learner with stable levels motivation, the learner has no ability to control the extraneous cognitive load. If the internal cognitive load increases and the external cognitive load decreases, the intrusive cognitive load becomes very high because the learner has to allocate a large proportion of the working memory to deal with the scientific material.

Modular thinking in solving inferential statistics problems: Stereotyped thinking is an approach to thinking based on a prosaic fringe of aspects of the world around us. It aims to integrate multiple and diverse perspectives to provide a comprehensive understanding of insights beyond those provided by each perspective separately. It focuses on studying the whole rather than understanding its parts. This allows a better understanding and perception of human, social, biological, and engineering systems, especially when they are characterized by high levels of complexity. Stereotypical thinking is receiving more attention in different areas as a necessary skill for dealing with contemporary problems. Notable areas include management (Salado, Chowdhury & Norton, 2019).

Stereotyped thinking is based on finding routine mathematical operations studed by the learner at school. It refers to learning clues and similarities to solve problems successfully (Foong & Koay, 1997). While solving mathematical problems with creative ideas helps to master a skill the learner has not been trained on, and then leads him or her to creativity rather than stereotypes of thinking (Salado et al., 2019).However, when the learner begins to learn mathematics by merely acquiring traditional mathematical procedures, this results in the  development of defensive strategies that usually end with poor performance, and some negative effects of using stereotyping when writing mathematical proof (Leahy & Sweller, 2019).

Stereotyped thinking is defined as the processes of self-classification and initial modeling of the expression of behaviors in situations of personal uncertainty and non-integration with the compulsive context that decreases perception and motivation. Uncertainties in understanding the context are reduced whenever learning is collaborative and in the light of actions of an association in which self-motivation and self-evaluation merge and the mathematically desired derivation occurs (Hogg, 2000). The researcher defines it procedurally as the score the learner obtains on the scale of stereotypical thinking in solving mathematical problems.

The nature of statistical problems and stereotypical thinking: Statistical problem-solving needs mental representations that differ in accessibility and work within goal systems. The implicit nature of goal activation and its effectiveness can be illustrated not only in the heart of the influence of stereotypical thinking on how one responds to members of stereotypical groups, but also in the implicit control of stereotypical activation in the first place (Moskowitz & Ignarri, 2009). Stereotyped thinking is divided into two types: explicit stereotyped ideas and implicit stereotyped ideas. Implicit stereotypes are characterized by bias, but these bias decreases when evaluating these actions explicitly among learners (Park, Felix & Lee, 2007).

Stereotyped threats theory: There is evidence that stereotype threat interferes with performance and achievement (Carr & Steele, 2009). Osborne (2001) concluded that many emotional and cognitive – anxiety mediators such as the increase in the level of arousal, changing performance expectations, working-memory interference, and cognitive load are influential variables in stereotypical thinking.According to Schmader, Johns & Forbes (2008), the stereotypical activation of trivial mathematical ideas and the working memory undermines impulse, emotional, and cognitive processes, causing poor performance in a cognitive context characterized by intellectual stereotyping. When the learner is faced with a new statistical-oriented research problem, he or she undergoes a state of imbalance that disrupts cognitive monitoring and interpretive processes, causing cognitive load.

The more statistical problems are associated with previously acquired cognitive schemas, one exhibits a combination of high performance and low mental effort (Seufert, 2018; Van Gog & Paas, 2008), since the information to be processed does not exceed a template already stored in the form of a cognitive schema in long-term memory, even if the schema is in the form of texts and graphs (Chandler & Sweller, 1991). Stereotypical thinking also carries a hidden self-threat to its over-reliance on the framework of traditional solutions (Seitchik, Jamieson & Harkins, 2014).

Reasons for doing the study: The study is justified by the fact that stereotypical expectations are different for both genders in Math and Science tests. Stereotypical thinking deficits increase when girls work alone compared to mixed-gender groups (Huguet & Régner, 2007). The researcher also proceeded from studies (Baars et al., 2017; Redifer et al., 2019) that confirmed that problem solving helps reduces stereotypical thinking, improve observation accuracy, and enhance personal judgments by increasing age. The study variables were related to secondary school students, while stereotypical thinking was found that females more than males in this regard. Therefore, hypotheses of the study were formulated for female students in the Department of Psychology, Faculty of education in Ismailia. .

Research motivation: The study is based on the premise that stereotypes are different for both genders in math and science tests. Stereotypical thinking deficits increase when girls work alone compared to mixed groups of both genders (Huguet & Régner, 2007). The researcher also started from a study that confirmed (Baars et al., 2017; Redifer et al., 2019) that problem-solving helps to reduce stereotypical thinking and improve the accuracy of observation and the growth of individual judgment by increasing age. The stereotyping has found that females are higher than males in this regard. Then the hypothesis study on females from the Psychology Department students was conducted.

Statement of the Problem: Being a lecturer in the Department of educational psychology and teaching the psychological statistics course for students of the second division of psychology for two years, the researcher noticed that in the academic year 2017/2018 the tests were essay type and students were trained to solve mathematical and statistical problems in this course with high levels of thinking and that students ,who tried especially in open-ended problems that require the learner to impose questions and assumptions and test them using the six test steps, got high score.As for the 2018/2019 year to which the results were applied, the change in the general policy of the tests was observed, due to the nature of the course of psychometric statistics requiring higher levels of thinking. The researcher tried to diversify the test questions to keep balance between the objective questions and the methodological problems requiring the use of the six test steps in which the questions are different from those familiar to the learner. Specifically, the researcher noticed the following:

1. Some students replaced some variables in the research statistical questions that were given to him with other variables not included in the question and provided the solution based on the new variables.
2. Some students used the same variables given in questions while ignoring the level of measurement needed to test the difference statistically and complete solution of the problem in statistics.
3. Some students that replaced the variables in the first case adopted a certain cut-off point and then crossed out the variables they replaced and changed the results they provided in the first case and completed the solution.

It is noted that the different nature of the research questions to be answered from the learner brought about an internal and external cognitive load that resulted in the implicit or explicit stereotypes shown in the previous three cases.

Objectives of the study: The ultimate objective of the current study is to assess the relationship between types of cognitive load and stereotypical thinking in solving problems in the course of Inferential Statistics among the students of the psychology department at the Faculty of education in Ismailia.

Significance of the study:The study was hoped to guide the faculty members to identify the patterns of cognitive load causing stereotypical thinking during the solution of mathematical problems during Inferential Statistics course among students of the Department of psychology at the Faculty of education in Ismailia. It would help modify the teaching and learning methods and guide students to interact with rich activities and different types of creative problem-solving techniques so as to reduce cognitive load they undergo on solving mathematical problems.

Hypotheses:Two hypotheses were formulated and tested:

• There is a correlation between patterns of cognitive load and stereotypical thinking in problem-solving in the Inferential Statistics Course among Psychology Department students at the Ismailia College of Education.
• The contribution of cognitive load patterns varies in predicting stereotypical thinking in problem-solving in the Inferential Statistics course.

METHODS

Participants: Seventy-six 2^nd year students (70 females, M_age = 19.81, SD = 0,43), enrolled in Psychology department, College of Education, , were chosen intentionally.

Instruments:To collect the target data the researcher prepared the following

The instruments were used:The cognitive load scale: It is a 14-item scale assessing the mental effort exerted on solving statistical problems in the working memory. The researcher developed a scale considering Sweller’s (2011) modified cognitive load theory. The scale was a five- Likert point scale (1= never, 2= rarely, 3= sometimes, 4= often, 5= always). stereotypical thinking scale: It is a 7-items scale assessing the stereotypes way of thinking while problem-solving in inferential statistics. The researcher developed the scale based on the studies of Foong & Koay, (1997); Salado, Chowdhury & Norton, (2019) .

Scale development:Cognitive load scale: A total of 76 students were recruited in testing validation and reliability assessment. Exploratory factor analysis resulted in a three-factor solution. Bartlett’s Sphericity test and Keiser-Meyer-Olkin (KMO) were calculated as measures of the suitability of data for structure detection. For data to be considered suitable, Bartlett’s test should be significant and the KMO value should be over .80 (Bartlett, 1954; Kaiser & Rice, 1974). The data were suitable for factoring as Bartlett’s test was significant (p < .001) and the KMO value was .65 showing accepted values for factorial analyses. EFA was conducted for the categorical data using a Principal axis factoring approach. Promax rotation method was used to obtain factor loading as (table 1).

Table   1. factor loading and attribution of each item based on factor analysis.

Items	Factor loading
	Intrinsic load	Extraneous load	Germane load
1)       I feel confused in determining the appropriate statistical test for the answer			0.48
2)       I am solving the vocabulary of the statistic test	0.33
3)       I look for complementary approaches when choosing the best solution	–	–	–
4)       Offer different solutions to the same statistical questions	0.59
5)       Use the properties of each statistical techniques to determine the most appropriate method of solution	0.58
6)       Start solving problems of statistical testing, link each issue with mathematical blocks familiar to me	0.58
7)       I need to study solved problems to understand different solutions to problems			0.49
8)       I rearrange questions by test			0.32
9)       I am afraid of frying pans issues on which all the statistic exams are presented		0.83
10)   I am not afraid of statistical methods			0.69
11)   I am powerless when asked to suggest methods and numbers for solving statistical problems		0.70
12)   I prefer to choose statistical methods to solve than my restriction to specific methods	–	–	–
13)   I feel that every statistical method has its distinctive matters	–	–	–
14)   I imagined in a way that enables me to develop renewed solutions to statistical issues	0.79
Eigenvalue Variance explained	2.20 10.69%	1.89 13.48%	1 4.42%

The factor loading ranged from 0.33 to 0.79 for the intrinsic load, 0.73 to 0.80 for the extraneous load, and 0.32 to 0.69 for the germane load. Items 3, 12, and 13 were not attributed to any of the factors. The main explanation for this finding is that items related to statistical techniques could be used in problem-solving. These items reflected an overlap between the three factors of the cognitive load. The internal consistency of the cognitive load scale was adequate with a Cronbach’s alpha of 0.71 for intrinsic load, 0.79 for the extraneous load, and 0.55 for the germane load.

The stereotypical thinking scale: EFA resulted in 1^st order general factor solution. Bartlett’s Sphericity test was of statistical significance (p < .001) and the KMO was .80, showing meritorious value for factor analysis. For the categorical and ordinal data, EFA was performed by a principal axis factoring approach. Factor loading was obtained by using Promax rotation solution as (table 2).

Table 2. factor loading, and attribution of each item based on factor analysis.

Items	Factor loading	Communalities
1)       I fail when I try to improve my image of others about my performance	0.37	0.16
2)       I worry about my learning path due to my poor performance in statistics	0.85	0.73
3)       I am afraid of the effect of the statistic on my future performance in college	0.89	0.80
4)       I am afraid of confirming the stereotype of my performance to prevent me from achieving my dream	0.77	0.59
5)       I feel powerless if the operative question differs from what I studied	0.73	0.55
6)       I am looking to compile statistical issues into ideas before I study them	0.71	0.50
7)       I use a distinct sign for every statistical test that characterizes my problem	—	0.06
Eigenvalue Variance explained	2.77 39.50%

The factor loading ranged from 0.37 to 0.89. Item 7 was excluded because it might cause the shyness of the learner to respond to it, even if it is true that there are indicators that distinguish each problem from the other. The internal consistency of the stereotypical thinking scale agrees with a Cronbach’s alpha of 0.78. Alpha if item deleted ranged from 0.68 to 0.84.

Design: The study relied on the correlational approach to verify the relative contribution of the cognitive load in predicting typical thinking among students of the 2^nd year, Department of Psychology, Ismailia College of Education, in the  Inferential Psychological Statistics Course.

Procedures and Data Analysis: Data analysis was performed by IBM SPSS V.20 statistics for windows. Exploratory factor analysis was used to obtain factor loading by the Promax rotation method. Internal consistency was assessed. Statistical significance was set at 0.05. The relationships between cognitive load patterns and stereotypical thinking were evaluated using the Pearson correlation matrix. Multiple regression was used for testing hypotheses.

RESULTS AND DISCUSSION

Correlation between cognitive load patterns, and stereotypical thinking: The relationship was moderate and strongest statistically significant correlations for extraneous cognitive load (r = 0.349, P = 0.000) and germane load (r = 0.653, P = 0.000). No correlation was found between intrinsic load and stereotypical thinking (table 3).

Table 3. Pearson’s correlations between Cognitive load and Stereotypical thinking.

Variables	Stereotypical thinking
	r	p
Intrinsic cognitive load (ICL)	0.026	>0.05
Extraneous cognitive load (ECL)	0.394	<0.05
germane cognitive load (GCL)	0.653	<0.05

The correlation between the extraneous load and stereotypical thinking is attributed to the fact that when students read inferential statistics problems, they compare them with the previously stored templates of problems and issues in the working memory. Some parts of this led them to think stereotypically as Park, Felix & Lee (2007) argued.The study assumed that extraneous load is the result of other factors that relate to individuals or factors related the assigned task (as in the circumstances of the second-semester test). It also confirmed that the complex implicit nature of cognitive structures had negative effects on those with stereotypical thinking in statistical problem-solving, as indicated by Redifer et al. (2019).

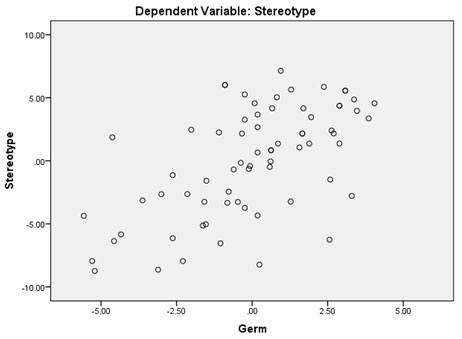
Regression analysis:The multiple regression coefficients were 0.253 (p ˂ 0.05) and 0.577 (p ˂ 0.05) respectively (Table 4). Fig. 1 shows the relationship in the scatter plot. A positive, statistically significant relationship between extraneous and germane cognitive load patterns and stereotypical thinking (Table 4). The relationships between intrinsic load and stereotypical thinking were not significant in the multiple regression model.

Table 4. Pearson’s correlations between Cognitive load and Stereotypical thinking.

Dependent variable: stereotypical thinking
Independent variables	coefficient	(95% CI)	P-Value
intrinsic cognitive load (ICL)	-0.005	-0.23-0.22	0.958
Extraneous cognitive load (ECL)	0.253	0.21-1.40	0.008
germane cognitive load (GCL)	0.577	0.74-1.45	0.007

Figure 1: scatter plot for the intrinsic load and stereotypical thinking.

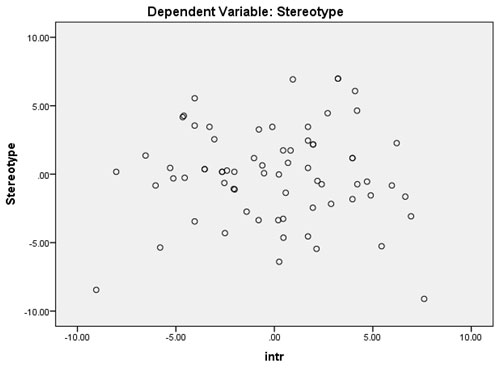
Figure 2: scatter plot for the extraneous load and stereotypical thinking.

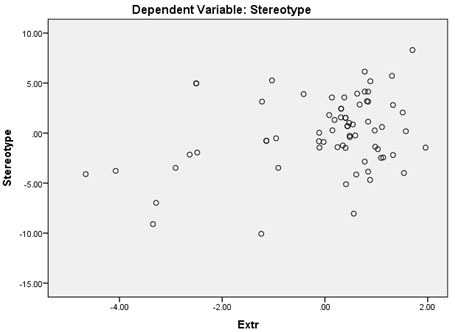
Figure 3: scatter plot for the germane load and stereotypical thinking.

The results indicate that cognitive load patterns can contribute to the prediction of stereotyped thinking in solving mathematical problems in the students of the psychology department at the Faculty of Education, Suez Canal University in the course of psychological statistics. The study found that the intrusive load as a predictor of stereotypical thinking in solving mathematical problems in the Psychological Inferential Statistics Course resulted from the lack of information in long-term memory that satisfies the process of creating and processing information in a sequential manner needed for the formation of proofs and the solution of mathematical problems which is supported by the study of Leahy & Sweller (2016).

Results also revealed that the apparent stereotyping of the formation of unwanted magmatic schemes in the learner was a result of the seriousness and novelty of ideas of mathematical matters which helped to find future solutions to problems that seemed different in their being. This result agrees with the conclusions of Leppink, (2017) and Sweller (2011).In addition, the nature of the problems posed by the researcher in the test of Psycho-deductive statistics was clearly prolonged by employing a certain method that develop in the familiar series of solutions provided by the students. In addition, the researcher presented the data of the issue in new ways that helped to solve mathematical problems and justified the inability of the internal load as a predictor of stereotypical thinking. This prevented the interaction between the elements required in the solution which were provided in advance to the students. This result agrees with the conclusions of Sweller, 2011).

The study also confirmed that that stereotyped thinking resulted of the failure to create and process charts within the working memory, the failure to make changes in the information structure previously stored in the working memory, regardless of the constraints of working memory, as concluded by Leahy & Sweller (2016, 2019).Deficiencies in thinking processes were characterized by weak formations of cognitive structures that rely on the initial information included in the statistical problems. This information requires secondary types of information retrieved from the long-term memory to be organized with with primary information (data) to solve the assigned problems (Chen et al., 2017).

Also, the external cognitive load was limited and did not require the interactions of the elements during the solution as the researcher administered the test of Psychological Inferential Statistics in a way which enabled students to deal with the statistical problems winch were different from those studied before, i.e. the effect of the external cognitive load was adjusted and this justifies the lack of statistical significance. Problem-solving processes did not entail the development of a link and infrastructure of the new issue and therefore was not affected by the working memory capacity and the necessary address information. This result is consistent with that of Chen et al., (20170 and Sweller, (2011).The study also led to the conclusion that the interactions between the discrete elements in the new formulations to solve the problem were fictitious as the researcher gave the solution method so as not to confuse learners while answering the test. This was another reason why the external cognitive load was not indicative, as revealed by Leppink, (2017) and Tricot & Sweller,( 2014).

This result may be attributed to the fact that the researcher tried to reduce the size of the differences that appear in the elements of the problem in order to decrease the number of sub-series of the solution inferred in the accepted methods of solution, which reduced the number of common errors. Results also indicate that the internal and external cognitive load was not inhibited by stereotypical thinking and this is consistent with (Orru & Longo, 2018; Redifer et al., 2019). The increase in the internal cognitive load with more creative thinking, may mean that mathematical problems in the statistics course were familiar to students.These results agree with the findings of Paas & Van Gog (2006) that the decrease in the external cognitive load may due to training on complex mathematical practical examples. They also agree with Sweller (2010) that the intruder load increases twice more than the external load. Moreover, results are consistent with the results of Foong & Koay (1997) in that the cognitive load decreases using similarities and clues in solving mathematical problems.

The results are also consistent with the conclusions of Orru & Longo (2018) and Peck et al., (2018) in that the intrusive load depends primarily on the learners abilities such as motivation regardless of the nature of the learning material. The greater the internal cognitive load, the more thinking processes become critical, deductive and creative. Mathematical problems posed by the researcher during Inferential Statistics course entailed creative intellectual products. This load required internal knowledge depend on the difficulty of the mathematical tasks and its value was not significant which means that the tasks needed only stereotypes of thinking. This result is consistent with the results of Redifer et al., (2019) and Seufert (2018). The study have some limitations including the fact that its results cannot be generalized to males studying the Inferential Statistics Course because the deficit in stereotypical thinking increases among females than males. Caution should be taken on applying the results to graduate students at different levels (educational diplomas, master’s, doctorate) where stereotypical thinking and personal judgment decrease with increasing age.

ACKNOWLEDGEMENTS

The authors would like to thank his colleagues Dr. Abdullah El-Anezy for useful discussions and their psychological perspectives and implications.

Conflict of Interest: Author declares no conflicts of interests to disclose.

Ethical Clearance Statement: The Current Research Work Was Ethically Approved by the Institutional Review Board (IRB) of Suez Canal University, Ismailia (41522), Egypt.

REFERENCES

Baars, M., Van Gog, T., de Bruin, A., & Paas, F. (2017). Effects of problem-solving after worked example study on secondary school children’s monitoring accuracy. Educational Psychology, 37(7), 810-834.

Bartlett, M. S. (1954). A note on the multiplying factors for various χ2 approximations. Journal of the Royal Statistical Society Series B, 16, 296–298. https://doi.org/10. 2307/2984057.

Carr, P. B., & Steele, C. M. (2009). Stereotype threat and inflexible perseverance in problem-solving. Journal of Experimental Social Psychology, 45(4), 853-859.‏

Chandler, P., & Sweller, J. (1991). Cognitive load theory and the format of instruction. Cognition and instruction, 8(4), 293-332.

Chen, O., Castro-Alonso, J. C., Paas, F., & Sweller, J. (2017). Extending cognitive load theory to incorporate working memory resource depletion: evidence from the spacing effect. Educational Psychology Review, 1-19.‏

Chen, O., Retnowati, E., & Kalyuga, S. (2019). Effects of worked examples on step performance in solving complex problems. Educational Psychology, 39(2), 188-202.

Chinnappan, M. (2010). Cognitive load and modeling of an algebra problem. Mathematics Education Research Journal, 22(2), 8-23.‏

Foong, P. Y., & Koay, P. L. (1997). School word problems and stereotyped thinking. Teaching and Learning, 18(1), 73-82.‏

Fuchs, L. S., Fuchs, D., Malone, A. S., Seethaler, P. M., & Craddock, C. (2019). The Role of Cognitive Processes in Treating Mathematics Learning Difficulties. In Cognitive Foundations for Improving Mathematical Learning (pp. 295-320). Academic Press.‏

Goel, L., & Schnusenberg, O. (2019). Why Some People Multitask Better Than Others: Predicting Learning. Information Systems Management, 36(1), 15-23.‏

Hogg, M. A. (2000). Subjective uncertainty reduction through self-categorization: A motivational theory of social identity processes. European review of social psychology, 11(1), 223-255.

Hsin, I., & Paas, F. (2015). Effects of computer-based visual representation on mathematics learning and cognitive load. Journal of Educational Technology & Society, 18(4), 70-77.‏

Huguet, P., & Régner, I. (2007). Stereotype threat among schoolgirls in quasi-ordinary classroom circumstances. Journal of Educational Psychology, 99(3), 545-560.

Kaiser, H. F., & Rice, J. (1974). Little Jiffy, Mark Iv. Educational and Psychological Measurement, 34, 111–117. https://doi.org/10.1177/001316447403400115.

Leahy, W., & Sweller, J. (2016). Cognitive load theory and the effects of transient information on the modality effect. Instructional Science, 44(1), 107-123.‏

Leahy, W., & Sweller, J. (2019). Cognitive load theory, resource depletion, and the delayed testing effect. Educational Psychology Review, 1-22.‏

Leahy, W., & Sweller, J. (2019a). The centrality of element interactivity to cognitive load theory. Advances in Cognitive Load Theory: Rethinking Teaching, 221.‏

Leppink, J. (2017). Cognitive load theory: Practical implications and an important challenge. Journal of Taibah University Medical Sciences, 12(5), 385-391.

Moskowitz, G. B., & Ignarri, C. (2009). Implicit volition and stereotype control. European Review of Social Psychology, 20(1), 97-145.

Neumann, E., & Russell, P. (2019). Is Working Memory Load Irrelevant to Inhibitory Cognitive Control in Negative Priming?.‏

Norouzi, E., Vaezmosavi, M., Gerber, M., Pühse, U., & Brand, S. (2019). Dual-task training on cognition and resistance training improved both balance and working memory in older people. The Physician and Sportsmedicine, 1-8.‏

Orru, G., & Longo, L. (2018, September). The evolution of Cognitive Load Theory and the measurement of its intrinsic, extraneous, and germane loads: a review. In International Symposium on Human Mental Workload: Models and Applications (pp. 23-48). Springer, Cham.‏

Osborne, J. W. (2001). Testing stereotype threat: Does anxiety explain race and sex differences in achievement?. Contemporary Educational Psychology, 26(3), 291-310.‏

Paas, F., & Van Gog, T. (2006). Optimizing worked example instruction: Different ways to increase germane cognitive load.

Paas, F., Tuovinen, J. E., Tabbers, H., & Van Gerven, P. W. (2003). Cognitive load measurement as a means to advance cognitive load theory. Educational psychologist, 38(1), 63-71.

Park, J., Felix, K., & Lee, G. (2007). Implicit attitudes toward Arab-Muslims and the moderating effects of social information. Basic and Applied Social Psychology, 29(1), 35-45.

Peck, T. C., Doan, M., Bourne, K. A., & Good, J. J. (2018). The Effect of Gender Body-Swap Illusions on Working Memory and Stereotype Threat. IEEE transactions on visualization and computer graphics, 24(4), 1604-1612.

Redifer, J. L., Bae, C. L., & DeBusk-Lane, M. (2019). Implicit Theories, Working Memory, and Cognitive Load: Impacts on Creative Thinking. SAGE Open, 9(1), 2158244019835919.

Salado, A., Chowdhury, A. H., & Norton, A. (2019). Systems thinking and mathematical problem-solving. School Science and Mathematics, 119(1), 49-58.‏

Schaper, P., & Grundgeiger, T. (2019). Author accepted manuscript: Commission Errors with Forced Response Lag. Quarterly Journal of Experimental Psychology, 1747021819840583.‏

Schmader, T., Johns, M., & Forbes, C. (2008). An integrated process model of stereotype threat effects on performance. Psychological Review, 115(2), 336.‏

Seitchik, A. E., Jamieson, J., & Harkins, S. G. (2014). Reading between the lines: Subtle stereotype threat cues can motivate performance. Social Influence, 9(1), 52-68.

Seufert, T. (2018). The interplay between self-regulation in learning and cognitive load. Educational Research Review, 24, 116-129.‏

Sweller, J. (1988). Cognitive load during problem-solving: Effects on learning. Cognitive science, 12(2), 257-285.‏

Sweller, J. (1994). Cognitive load theory, learning difficulty, and instructional design. Learning and instruction, 4(4), 295-312.

Sweller, J. (2010). Element interactivity and intrinsic, extraneous, and germane cognitive load. Educational psychology review, 22(2), 123-138.

Sweller, J. (2011). Cognitive load theory. In Psychology of learning and motivation (Vol. 55, pp. 37-76). Academic Press.‏

Sweller, J. (2015). In academe, what is learned and how is it learned? Current Directions in Psychological Science, 24(3), 190–194.

Sweller, J., Kirschner, P., & Clark, R. E. (2007). Why minimally guided teaching techniques do not work: a reply to commentaries. Educational Psychologist, 42(2), 115–121.

Treffers, A. (2019). Direct instruction and problem-solving: Critical examination of Cognitive Load Theory from the perspective of mathematics education. The Mathematics Enthusiast, 16(1), 607-620.

Tricot, A., & Sweller, J. (2014). Domain-specific knowledge and why teaching generic skills does not work. Educational Psychology Review, 26(2), 265–283.  https://doi.org/10.1007/s10648-013-9243-1

Van Gog, T., & Paas, F. (2008). Instructional efficiency: Revisiting the original construct in educational research. Educational Psychologist, 43(1), 16-26.

Wieth, M. B., & Burns, B. D. (2014). Rewarding multitasking: Negative effects of an incentive on problem-solving under divided attention. The Journal of Problem Solving, 7(1), 7.‏