aDepartment of Biotechnology, IMS Engineering College, Ghaziabad, UP, India
bChemical Engineering Department, Indian Institute of Technology Roorkee, Roorkee 247667, Uttarakhand, India
c*Department of Biotechnology, Noida Institute of Engineering & Technology, Greater Noida, UP, India
Article Publishing History
Received: 25/07/2016
Accepted After Revision: 05/09/2016
Different phases of the Gliomastix indicus growth curve and the production of á-amylase using solid-state fermentation process based on variation in dry weight was mathematically modeled. The result of the study reveals that the growth of the fungal cells and the production of á-amylase on a mustard oil cake as solid substrate could be expressed by simple models incorporating the mathematical definition of each phase and the variation in dry substrate weight over the incubation time. The growth kinetics of G.indicus could be described by the mathematical modeling parameters regarding maximum specific growth rate and maximum biomass concentration obtained by fitting the experimental data to the logistic model. Experimental data collected from a series of batch fermentations process were collected for 10 days (240 hrs.) and used to propose the mathematical models. Experimental observations, and predicted models made it possible to conclude that these models can be successfully employed to represent the biomass growth and á-amylase production in solid-state fermentation processes.
Solid State Fermentation, Mathematical Modeling, Biomass Growth Kinetics, Production Kinetics
Mishra S. K, Kumarb S, Singh R. K, Kumar S. Mathematical Modeling of Microbial Growth and Production Kinetics for á-Amylase Production Using Mustard Oil Cake as Solid Substrate. Biosc.Biotech.Res.Comm. 2016;9(3).
Mishra S. K, Kumarb S, Singh R. K, Kumar S. Mathematical Modeling of Microbial Growth and Production Kinetics for á-Amylase Production Using Mustard Oil Cake as Solid Substrate. Biosc.Biotech.Res.Comm. 2016;9(3). Available from: https://bit.ly/2MI3zL2
Introduction
Solid state fermentation process (SSF) involves the growth of microorganisms on a moist insoluble solid substrate in the absence or sometimes nearly absence of free liquid (Mitchell et al 2002; Pandey 2003). The level of water available for growth of microorganism in SSF is low which makes it suitable for the growth and cultivation of fungi (Pandey 2003; Cannel and Moo Young 1980). The solid state fermentation (SSF) is used in a number of fermentation industries for the production of enzymes, organic acids, and other bioactive compounds. Fermentation processes can be improved by using suitable methods to estimate the biomass and other main process variables resulting in the investigation of the associations between growth kinetics and the fermentation product. In SSF precise estimate is complicated because of the difficulty in the separation of biomass from the fermentation media. Therefore, appropriate data are not accessible concerning the kinetics and biomass in SSF.
Substrate moisture content, temperature and, biomass have been found as the critical variables that affect growth of microorganism and enzyme production (Khanahmadia et al.2006; Desgranges et al.1991) For any SSF these parameters must be controlled during the entire fermentation processes. Several approaches have been proposed by researchers for indirect measurements of biomass formation, such as estimating the production of primary metabolic product (Desgranges et al.1991; Okazaki et al.1980) amount of carbon dioxide production (Raimbault 1998), the variation in the electrical conductivity of the biomass and solid substrate (Carriazalez et al.1981) and the changes observed in the color of the fermentation medium. Other than these methods, a direct method of viable cell count can also be used to estimate the amount of biomass formation.
There are consequential difficulties that have been observed with the direct measurement of cell biomass in SSF systems therefore a weighing method could provide a significant method in kinetic studies of such processes. Bioprocess modeling including cells and cultures can be of significant importance in optimizing and controlling actual production process of biomass and product (Curien et al. 2003; Grosz and Stephanopoulos 1999). Several challenges have been observed at each stage in the development of models of enzyme production kinetics (Copella and Dhurjati 1989; Thilakavathi et al. 2007). Earlier, a kinetic model has been developed for batch fermentation for lactic acid production using cane-sugar molasses by Enterococcus faecalis. Parameters of the kinetic model have been determined and validated based on experimental data by using genetic algorithm (Nandsana and Kumar 2008, Gelatin et al. 2015).
The effect of temperature and substrate moisture content on the growth and production of amylase, protease and phytase by Aspergillus niger during SSF was investigated and a mathematical model for the kinetics of growth and enzyme production were developed earlier. A mathematical model to describe the kinetics of enzyme production by the filamentous fungal sp. Trichoderma harzianum was developed using sugarcane bagasse as solid substrate for the production of cellulase, beta glucosidase and xylanase. In all the studies, it has been found that temperature and substrate moisture content of the media play a significant role for the growth of microorganism and enzyme production (Saithi et al. 2016).
In recent years, SSF has gained renewed interest from researchers for the production of enzymes which have industrial important in view of its economic and engineering advantages. In this work we are proposing a mathematical model can be used as an aid for improving the design and control of SSF processes. The major objective of this study was to identify and develop model for the growth, stationary, and death phases of the growth curve and á-amylase production kinetics during SSF processes using a comparatively simple weighing method by using G. indicus as a fungal strain. The knowledge gained from our research work may contribute to the understanding and control of SSF processes for large scale enzyme production using fungal strain.
Material And Methods
Inoculum preparation: The microorganism Gliomastix indicus (MTCC 3869) was procured from the Institute of Microbial Technology (IMTECH) Chandigarh India. G. indicus comprises the properties of filamentous fungi and rapidly grows on all common mycological media such as malt extract, potato dextrose agar etc. This fungal strain was maintained on the potato dextrose agar (PDA) medium which contains; potatoes 200g/l, dextrose 20g/l and Agar 15g/l. The pH of the medium was adjusted to 6 by using 1N NaOH. The organism was maintained by the serial transfer on the PDA medium after every fortnight and incubated at 30°C.
Inoculum was prepared by transferring 5ml suspension culture, into 250ml conical flask containing 95ml of sterile inoculum medium. The composition of the inoculum medium was (g/l): Glucose (20g/l), NH4NO3 (3g/l), MgSO4.7H2O (0.5g/l), KCl (0.5g/l), K2HPO4 (1g/l), FeSO4.7H2O (0.01g/l), with a pH of solution 6.0. The flasks were incubated on a rotary shaker at 200rpm at 28°C for 48 hrs (Nagalaxmi et al. 2008; Kammoun et al 2008).
Cultivation of Fungal Strain: G.indicus was cultivated in SSF using mustard oil cake as solid substrate and moistened with distilled water (1:1.2). After autoclaving at 121˚C for 20 min, the culture medium was inoculated with 15% (v/v) of the above applied inocula and mixed thoroughly to ensure uniform distribution. The inoculated MOC was distributed in Petri dishes (8 cm in diameter) as follows: 1.0 cm average thickness of the culture medium, 10 g initial weight of inoculated medium per dish, 80% initial moisture content, and incubated at 30˚C for 0-240 hr. Dish samples were removed from the incubator at regular intervals for the determination of the number of viable cells, the total dry weight of the fermented substrate, and the production of á-amylase.
Analytical methods: Viable cell count: The viable bacterial count was determined by suspending the fermented substrate in peptone-phosphate buffer at a 1:10 ratio and shaking the suspension for 15 min, followed by serial dilution and plating onto plate count agar. The number of viable colonies in the fermented substrate after 96 h incubation at 30°C is reported as cfu/g.
Total dry weight: The total dry solid weight per dish was evaluated by drying at 80 ± 3°C to constant weight. Then the final dry weight was calculated and presented as the variation in the dry matter of the fermented wheat bran during the test as Wt.
á-amylase activity: Crude enzyme was extracted by mixing a known quantity of fermented substrate with distilled water in a 1:10 ratio on a rotary shaker (180 rpm) for 1 h. The slurry was squeezed through wet cheesecloth. Then the filtrate was centrifuged (10,000 × g, 10 min, 4 °C), and the clear supernatant was used as the source of the crude enzyme. The activity of -amylase was determined by the Bernfeld procedure using soluble starch (Qualigens) as a substrate (Bernfeld 1955). The reaction mixture was incubated for 15 min at 35˚C. One unit (U) of -amylase is defined as the amount of enzyme that releases 1 mol of reducing sugar as maltose per minute under the assay conditions and is expressed as U/g of dry fermented substrate.
Mathematical Model:The total weight of medium under SSF using MOC as solid substrate can be written as:
Total Wt (W) = Wt of Solid substrate(S)
+Wt of Biomass(B)+ Wt of Product(P) …(1)
![]()
The value of all the three parameters will change as the fermentation process progress. Hence above equation can be represented in differential form with respect to time. Therefore:
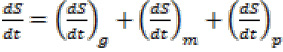
The substrate consumption rate by biomass will be different in different growth stages. Hence rate of substrate consumption with respect to time under different stages can be represented as:
![]()
The substrate consumption rate under different growth phase can be defined by either biomass growth equation and biomass yield coefficient or by using enzyme production equation and coefficient of yield (Amrane and Pregent 1994; Venkatesh et al 1993; Yeah et al. 1991)
As suggested by Hashemi et.al, the equation for the estimation of total biomass weight with respect to total medium weight can be represented as:
![]()
Furthermore, the equation for the estimation of total weight of product can also be represented as:
![]()
The above equations indicate that the amount of biomass and product concentration in the fermentation media can be estimated with the help of total value of W (Hashemi et al 2011).
Result And Discussion
Change in dry weight of medium during the fermentation process was calculated by substracting the weight recorded each day for continuously ten days from the initial weight i.e. W0=10.3 gm as shown in figure-1.
 |
Figure 1: Change in dry weight of medium observed during fermentation |
Growth phase was observed during the time period of 0-96 hr, stationary phase was found to be between 96-144 hr and subsequently decline phase was observed between 144-240 hr onwards. Now the values of growth phase and decline phase time frames were used to get the following equations respectively:
![]()
![]()
For the above Eqs. (6) and (7) coefficients of determinant (R2) were found to be 0.842 and 0.979. Along with it, the residual sums of squares (rss) for both the equations were 0.302 and 0.133 respectively. These values indicates that the Eqs. correlate the experimental data with a very approximation.
We can differentiate the Eqs. (6) and (7) with respect to time in order to get the relation for time dependent total medium weight degradation.
![]()
![]()
Eqs. (4) and (8) represent the equation for time dependent medium weight variation during biomass growth phase. Similarly, Eqs. (4) and (9) represent the equation for time dependent medium weight variation during biomass death phase. If the values of ã and ä are known, Eqs. (4) and (8) can be used for the calculation of biomass dry weight (B) during growth phase. Similarly, Eqs. (4) and (9) can also be used for the calculation of B during death phase.
The ã and ä values depend upon the selection of medium, choice of microorganism and the environmental conditions of fermentation process and it can be experimentally determined. For representation, the trend of growth curve based on the derived mathematical equation, ã/ä value was assumed to be 0.01. Initial biomass dry weight (B0)was experimentally determined and found to be 0.0042 g. Hence, Eqs. (8) and (4) will give:
![]()
Therefore, the final Eq. for biomass growth in growth phase will be:
![]()
As per the earlier assumptions t=96-144 were considered as stationary phase. Hence, B144 = B96 = 0.0052 g. Eqs. (9) and (4) will give:
![]()
Therefore, the final Eq. for biomass growth in death phase will be:
![]()
Using equation (11) and (13) and considering the time period of growth, stationary and death phase, the calculated values were plotted as shown in figure-2.
 |
Figure 2: Change in dry weight of biomass with time variation |
As shown in the figure, the calculated values on the basis of medium dry weight variation are in good correlation with the experimental values.
The mathematical model for á-amylase production kinetics in SSF is very convenient to represent the complex problem of such process. Here we are introducing a model for the prediction of á-amylase production kinetics on solid substrate using fungal strain G. indicus during fermentation process. Eq. (5) correlates the total product (P) with respect to fermentation time (t) using weight variation data of medium. The total product i.e. á-amylase was assayed for the entire period of fermentation process at regular time intervals. Following Eqs. (14), (15) and (16) were derived to represent the á-amylase production during growth phase, stationary phase and death phase respectively:
![]()
![]()
![]()
Form the above Eqs. (14), (15) and (16), the coefficients of determination (R2) were calculated as 0.99, 0.97 and 0.98 respectively. Figure-3 represents the correlation between experimental and predicted data calculated from the product kinetic mathematical model given above.
 |
Figure 3: Predicted and experimental á-amylase activity |
Conclusion
Because of the complexity of SSF systems, estimation of the biomass and product formation during the incubation time could give highly valuable information leading to a more comprehensive understanding of such complicated systems. We investigated a feasible approach for modeling the different phases of the fungal growth curve and production of á-amylase as product by G. indicus in a SSF process based on variation in dry weight. The result showed that fungal growth and the production of á-amylase on a MOC as solid substrate could successfully be modeled based on variations in solid substrate weight and can be used for large scale industrial production.
References
Amrane A, Prigent Y (1994) Mathematical model for lactic acid production from lactose in batch culture: model development and simulation. J. Chem. Technol. Biotechnol. 60:241–246
Bernfeld P (1955) Amylase and Methods Enzymol. 1:149–158
Cannel E, Moo-Young (1980) Solid-state fermentation systems. Process. Biochem. 4:2-7
Carrizalez V, Rodríguez H, Sardina I (1981) Determination of the specific growth of molds on semi-solid cultures. Biotechnol. Bioeng. 23:321–333
Coppella SJ, Dhurjati P (1989) A detailed analysis of Saccharomyces cerevisiae growth kinetics in batch, fed-batch, and hollow-fiber bioreactors. Chem Eng. J. 41:B27–B35
CurienG, Ravanel S, Dumas R (2003) A kinetic model of the branch-point between the methionine and threonine biosynthesis pathways in Arabidopsis thaliana. Eur. J. Biochem. 270 :4615–4627
Desgranges C, Georges M, Vergoignan C,Durand A (1991) Biomass estimation in solid state fermentation. II. On-line measurements, Appl. Microbiol. Biotechnol. 35:206–209
Desgranges C, Vergoignan C, Georges M, Durand A(1991) Biomass estimation in solid state fermentation I. Manual biochemical methods, Appl. Microbiol. Biotechnol. 35:200–
205
Gelain L, da Cruz Pradella JG, da Costa AC (2015) Mathematical modeling of enzyme production using Trichoderma harzianum P49P11 and sugarcane bagasse as carbon source. Bioresource technology. 198:101-107
Grosz R, Stephanopoulos G (1999) Physiological, biochemical, and mathematical studies of micro-aerobic continuous ethanol fermentation by Saccharomyces cerevisiae. III: mathematical model of cellular energetics and catabolism. Biotechnol. Bioeng. 36:1030–1040
Hashemi M, Mousavi SM, Razavi SH ,Shojaosadati SA(2011) Mathematical modeling of biomass and á-amylase production kinetics by Bacillus sp in solid-state fermentation based on solid dry weight variation. Biochemical Engineering Journal, 53:159-164
Kammoun R, Naili B, Bejar S (2008) Application of a statistical design to the optimization of parameters and culture medium for á-amylase production by Aspergillus oryzae CBS 819.72 grown on gruel (wheat grinding by-product). Bioresource Technology 99:5602-5609
Khanahmadia M, Roostaazad R,Mitchell DA, Miranzadeh M, Bozorgmehri R, Safekordi A (2006) Bed moisture estimation by monitoring of air stream temperature rise in packed-bed solid-state fermentation. Chem. Eng. Sci. 61:5654–5663
Mitchell DA, Berovic M, Krieger N(2002) Overview of solid state bioprocessing. Biotechnol Annu. Rev. 8:183–225
Nagalaxmi S, Vijayalakshmi M, Subrahmanyam A (2009) Gliomastix indicus sp nov. Current Trends in Biotechnology and Pharmacy 3:111-112
Nandasana AD, Kumar S (2008) Kinetic modeling of lactic acid production from molasses using Enterococcus faecalis RKY1. Biochemical Engineering Journal. 38:277–284
Okazaki N, Sugama S, Tanaka T (1980) Mathematical model of surface culture of koji mould. J Ferment. Technol. 51:471–476
Pandey A (2003) Solid-state fermentation. Biochem. Eng. J. 13:81–84
Raimbault M (1998) General and microbiological aspects of solid substrate fermentation. Electronic Journal of Biotechnology 3:26-27
Saithi S, Borg J, Nopharatana M, Tongta A (2016) Mathematical Modeling of Biomass and Enzyme Production Kinetics by Aspergillus niger in Solid-State Fermentation at Various Temperatures and Moisture Contents. J. Microb. Biochem. Technol. 8: 123-130
Thilakavathi M, Basak T, Panda T(2007) Modeling of enzyme production kinetics. Appl. Microbiol. Biotechnol. 73:991–1007
Venkatesh KV, Okos MR, Wankat PC (1993)Kinetic model of growth and lactic acid production from lactose by Lactobacillus bulgaricus. Process Biochem. 28:231–241
Yeh PLH, Bajpai RK, Iannotti EL (1991) An improved kinetic model for lactic acid fermentation, J. Ferment. Bioeng. 71: 75–77


