Michurinsk State Agrarian University, Michurinsk, Russia

Article Publishing History

INTRODUCTION

The purpose of harvesting sugar beet is to collect root crops, which provide the highest yield of sugar per hectare and minimal resource costs. The harvest and the quality of beets depend on the soil moisture in the second half of the growing season, its duration, and the quality of harvesting operations. For cereals, the harvest period can be easily set by the achieved ripeness phase. Sugar beet does not have such indicators. Beets can be considered ripe when root crops spend more energy reserves on the respiration for several days forming new reserve constituents by assimilation. But for healthy beets, this period comes in late autumn (Kuznetsov et al. 2020).

Sugar hybrids achieve an acceptable yield and maximum collection (yield) earlier than yielding hybrids. Harvesting machines must ensure the following agrotechnical and technological requirements: completeness of beetroots extraction from the soil (at least 98%); minimal losses (no more than 5% of sugar beetroots mass, and no more than 18% of tops); minimal contamination of beetroot (no more than 10% of beetroots, and 0.5% of tops).

Losses under optimal conditions of mechanized harvesting amount to 5%. Under unfavorable weather and soil conditions, they can reach 20% or more. When the soil is wet, the contamination of root crops and tops is higher, and the screening of soil impurities worsens.  High quality of work during harvesting should provide the optimal level of cutting the tops, a minimum of damage to the surface of root crops, a low proportion of soil stuck on root crops, and the least beet losses and destruction of the soil structure (Scott and Cooke 2012; Kleuker and Hoffmann 2021).

The costs of beet crops transportation to/from the plant depends on the weight of the soil stuck on root crops. Besides, the removal of the soil results in the worsening of its fertility (Tuğrula et al. 2012; Rajaeifar et al. 2019). For example, in Germany in 1991, the contamination of root crops amounted to 15%, the soil removal per hectare averaged seven tons. With an area under sugar beet in the amount of 570 thousand hectares, four million tons of soil were lost per year. For economic and environmental reasons, it is necessary to reduce the percentage of soil stuck on root crops by applying the following measures: selecting hybrids; conducting liming; ensuring high field germination; harvesting under optimal weather and soil conditions; choosing the optimal speed of the harvesting machines; providing additional cleaning sprockets, cleaning drums, and drive stages; adjusting the drum sugar beets cleaner to the average diameter of root crops (Haggar 2010; Tuğrula et al. 2012; Rajaeifar et al. 2019; Rajaeifar et al. 2019). The present work aims to improve the quality of cleaning sugar beetroot crops using a brush cleaner by developing a device for removing stuck soil from it when harvesting in conditions of high soil moisture.

MATERIAL AND METHODS

To calculate the theoretical speed, according to the impact theory and taking into account the elastic properties of the brush lint, one can use the formula

   (1)

where is the speed of impact at the moment of touching brush lint with the coil of the spring, used for cleaning, is calculated by the formula where  is the angular velocity of brush rotation (  R is the distance from the rotation axis of the brush drum to the point of impact, is the speed that occurs when the lint is straightened after escaping the root crop surface due to its elastic properties, m/s (Figure 2) (Solovyov and Kuznetsov 2016).

RESULTS AND DISCUSSION

In the design of mechanisms designed to extract root crops from the soil, digging plowshares and disk diggers were used. Given that the excavated root crops carry a large amount of soil and impurities, they undergo repeated cleaning on the separation devices of root harvesters. Combinations of different types of separating devices were used (cleaning screws, rod conveyors, rotating turbines, etc.). It was established that the cost of transporting root crops to sugar factories was 25-30% of the beet production cost.

The offered working tools for cleaning root crops (Figure 1) allowed continuing harvesting under complex conditions (at increasing soil moisture by up to 32%). Field trials showed a significant reduction of irreversible losses of topsoil when using upgraded working tools in comparison with the regularly used serial tools, as well as preserving their operational capacity at the highest soil moisture (up to 32%). Such conditions take up to a third of the harvesting time (Gil et al. 2013; Zavrazhnov et al. 2019).

Figure 1: Receiving rod conveyor of the ROPA Euro Tiger combine with installed brush drums

Considering the lint as a physical pendulum, it is possible to determine the period of its small oscillations T, 1/s according to the formula:

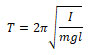          (2)

where I is the pendulum (lint) inertia moment relative to the rotation axis, kg*m², m is the mass of the pendulum (lint), kg, l is the distance from the rotation axis to the center of mass, m.

The length of the lint’s end travel path when cleansing the root crop can be represented as a sum of paths, traveled with the relative (with speed ω = at 57.39 rad/s) and transfer velocities (with velocity v) of the brush drum, on which the lint is fixed, and transported root crop (Figure 3).

Figure 2: Schematic diagram for determining the impact velocity: 1 – The center of impact of the lint on the spring coil; 2 – Extension spring; 3 – The trajectory of the lint point which impacts the surface; 4 – A lint bunch; 5 – Brush drum; 6 – The distance from the rotation axis of the brush drum to the center of impact.

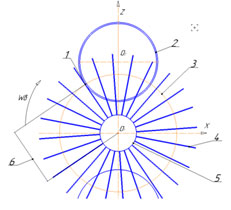
Figure 3: The schematic diagram for determining the length of a lint trace

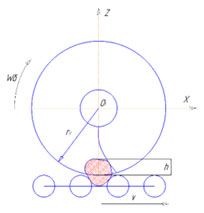
Considering these movements as independent, and summing up their results, we determine the length L of the lint trajectory during its contact with the root crop.

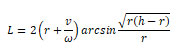       (3)

where v is the transfer velocity of the conveyor, m/s; r is the radius of the trajectory of the bending lint end, m; h is the maximum depth of immersion of the lint into the contamination array, m.

Based on formulas (2) and (3), the velocity can be determined as the ratio of the path to the time during which the lint is straightened:

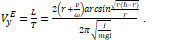    (4)

Thus, it is possible to calculate the velocity at which the brush lint impacts the coil of the spring, using formulas (1) and (4)

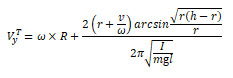    (5)

Finally, after some algebraic transformations, the theoretical impact velocity can be defined as

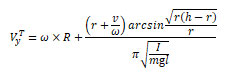       (6)

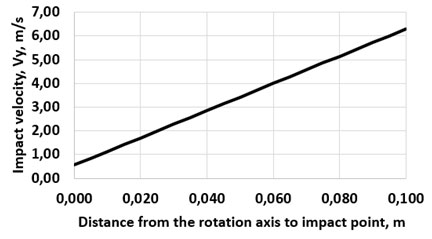
As a result, one can get the impact velocity depending on the distance to the impact point. Figure 4 shows that this velocity varies linearly, increasing as the distance to the impact point increases. The analysis of the dependence shows that this velocity can be most significantly influenced by the velocity of the conveyor, as well as the radius of the trajectory of the bending lint end, which directly depends on the diameter of the cylindrical brush (Kuznetsov et al. 2020; Kleuker and Hoffmann 2021).

Figure 4: The dependence of the impact velocity on the distance to the impact point

To determine the necessary impact velocity on the lint to clear it from the soil, it is necessary to know and take into account certain technological properties of the soil. In this case, these include the stickiness and frictional properties of the soil. At certain soil moisture, adhesion, and friction act together. When the soil slides over the surface of the working tool both processes manifest themselves simultaneously in the form of resistance to its sliding. Then the slip resistance is defined as

        (7)

where F_fr is the friction force of the soil on the surface of the working tool, N; F_ad is the adhesion force of soil to the surface material of the working tool, N.

It is logical to conclude that the theoretical impact velocity determined earlier must be equal or greater than theoretical impact velocity on the lint necessary to clean it from the soil, i.e.

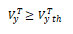      (8)

The maximum value of the friction force F_fr is achieved when sliding. The values of F_fr are within the range from 0.25 to 0.90, φ – 14…42. Besides, friction is significantly affected by soil moisture. At decreased moisture from 0 to 8-10%, moist soil does not stick to the surface. It is the case of true friction when the friction coefficient does not depend on humidity. The increase in F_fr is explained by the appearance of the molecular attraction forces of soil particles to the surface. When the moisture increases to 50-80%, it plays the role of a lubricant, decreasing F_fr. The friction force F_fr is influenced by the mechanical composition of the soil, i.e. the content of physical clay (particles less than 0.1 mm in diameter). To determine the stickiness, one can also use the well-known equation:

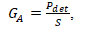     (9)

where P_det is the force required to detach from the soil, N; S is the area of the contact surface, m². This force can manifest itself in two ways.

– as a resistance when the soil slides on the surface of the working tools.

– as a resistance corresponding to the separation of solids in contact with working tools.

Slip resistance from sticking is determined by the formula, (10):

      (10)

where p₀ is the coefficient of specific adhesion in the absence of normal pressure, Pa; p is the coefficient of specific adhesion caused by normal pressure, Pa; S is the visible contact area, m²; N is the normal pressure force, N (Kuznetsov et al. 2020).

Comparing and  it is clear that the friction and adhesion laws have significant differences. Adhesion, unlike friction, depends not only on the normal pressure and the properties of the working surface of the material, but also on the contact area, and is manifested even in the absence of normal pressure N. The stickiness of the soil depends on the mechanical composition (dispersion), moisture content, the material of the surface of the working tool, and the specific pressure. As the dispersion increases, the stickiness increases, therefore clay soils are more sticky than sandy ones. Structureless soils are more sticky than structural ones. Stickiness manifests itself only at certain moisture:

– for structureless soils – at a relative humidity of 40-50%;

– for structural soils – 60-70%.

With increasing moisture, the stickiness first increases, and then decreases. The lint of the brush drum is made of nylon or dacron, which reduces the stickiness. The soil will stick to the working surface of the lint if the adhesion and friction forces between the soil particles or aggregates of the moving layer are less than the friction and adhesion forces between the soil and the working surface, i.e. 

    (11)

where C₀ is the soil adhesion coefficient, σ is the normal pressure Since the force is nothing but the pulse velocity or the rate of change in momentum mv, for further calculations we will express the impact velocity through the force. First, we write down the equation for determining the period of free vibrations for the lint fixed in the drum

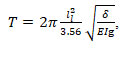      (12)

where  is the length of the lint, m; δ is the specific weight of the lint per unit length N/m⁴; E is the elastic modulus of the lint, Pa; I is the second moment of the lint, m⁴; g is the acceleration of gravity (g = 9.81 m/s²) (Kuznetsov et al. 2020; Kleuker and Hoffmann 2022). To make lint lagging behind the coil of the spring at the impact, the period of lint’s own vibration  should be greater than that of the coil against which the impact occurs.

Therefore, the period of free oscillation of the lint will be hence

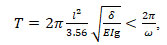       (13)

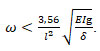        (14)

Now it is possible to determine the necessary and sufficient force impulse to clean the lint surface from the soil. We substitute the values of force and time, defined above (the period of free oscillation) into the following formula:

where t= T and F will take the values discussed above. Then the impulse offeree will be equal to

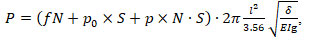       (15)

while the impulse offeree, necessary and sufficient for cleaning the surface of the lint from the soil must be greater than this value, namely:

       (16)

Based on the inequality (11), it is possible to determine the theoretical impact velocity on the brush lint, necessary for cleaning it from the soil

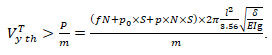       (17)

Substituting expressions (6) and (17) into formula (8), we get

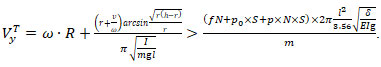         (18)

Based on the obtained formula, we construct a graph (Figure 5).

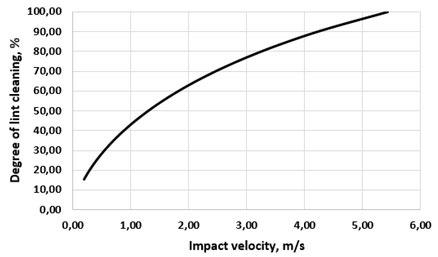
Figure 5: Dependence of the degree of lint cleaning on the impact velocity

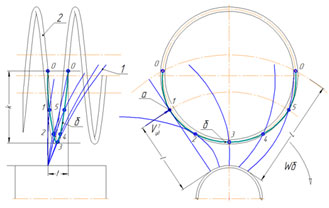
To determine the diameter of the wire for the spring, it is required to calculate the contact area between the lint and the coil of the spring. Based on the basic formulas of the contact interaction mechanics, and taking into account that a contact spot is fairly small, we make the following assumption: the lint and the spring wire are considered as the contact of two cylinders (Figure 6) crossing at an angle, and due to the small contact spot, we assume that the spot is circular. To determine the friction force (7), it is necessary to determine the normal force and the friction coefficient (Kuznetsov et al. 2020; Kleuker and Hoffmann 2022). The normal force is determined by

       (19)

where N(F) is the normal force, N; is the reduced modulus of elasticity, is the Gaussian radius of curvature (R₁ and R₂ are the radii of the cross-section of the lint and the coil of the spring, respectively, m); d is the penetration depth, m;

Figure 6: The schematic diagram of the interaction of the lint with the coil of the spring: 1 – lint, 2 –coil of the spring; a – the contact area; b – the trajectory of the lint motion in a contact with the coil of the spring, k – the contact spot of the lint when moving along the coil of the spring

The reduced modulus of elasticity is defined as:

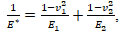      (20)

where E₁ and E₂ are the elastic moduli, Pa; and v₁ and v₂ are the Poisson coefficients of the bodies.

Let’s express  by transforming the formula (20)

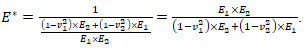              (21)

 The contact spot a is defined according to Since we previously assumed that the contact area (spot) is a circle, the contact area will be After the transformation, the contact area between the lint and the coil of the spring can be calculated using the formula The penetration depth will then be defined as 

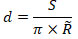            (22)

Substituting the expressions (21), (22) in the formula (19) we get

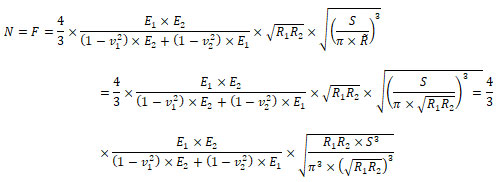               (23)

Finally, we get:

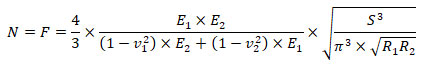                 (24)

The friction force at the contact interaction between the lint and the coil of the spring will be

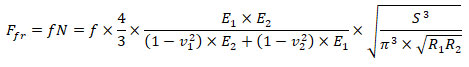                       (25) 

Let us express from the formula (25) the radius of the wire R₂ for making the spring

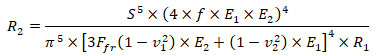                        (26)

The diameter of the wire will be equal to the double radius, respectively d = 2R2.

Next, we determine the main design dimensions of the cleaning static spring: d = 4 mm. According to the design dimensions of the brush and the condition of the static spring, we take the spring diameter D = 130 mm. The spring stiffness will be c₁ = 130/4 = 32.5 << 450, which corresponds to the condition of self-cleaning of the static spring. The dependence of the cleaning degree of the lint on the impact velocity of the coil of the spring, as well as on a distance (height) of the coil to the point of impact, and the distance from the lint attachment point to the point of impact is presented in the form of nomogram (Figure 7) (Rajaeifar et al. 2019; Rajaeifar et al. 2019).

Figure 7: Nomogram for determining the optimal parameters of the impact point location of the lint to
the coil of the spiral (the highlighted area corresponds to cleaning degree equal to 90-98%)

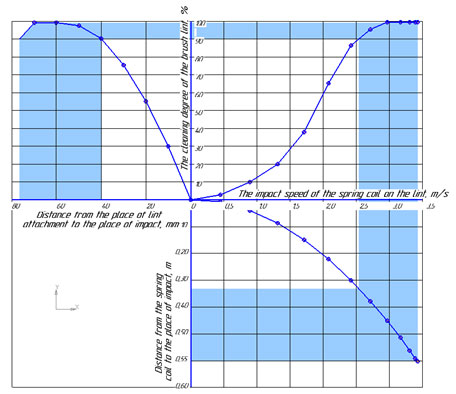
When conducting studies with heavy loamy chernozem soils with a moisture content of ≈28%, (which corresponds to the greatest stickiness) it is revealed that the minimum required brush lint impact velocity to separate soil from the coils of the spring is about ≈ 2.5 m/s. At the same time, the impact velocity of the brush lint should be large enough to separate the soil of maximum stickiness from the coil of the spring, however, it should not be greater than the velocity causing lint cutting, i.e., the velocity at which the brush lint is destroyed (Rajaeifar et al. 2019; Rajaeifar et al. 2019).

CONCLUSION

The findings of the present study obtained dependencies allowed revealing that with an increase in the height of the pendulum’s center of mass, the impact velocity on the lint also increases. The analysis of the dependence of the cleaning degree of the lint on the impact velocity shows that with an increase in the impact velocity on the lint, the cleaning degree increases. At velocities ranged from 0 to 1.7 m/s, the cleaning degree increases to 40%. With an increase in the velocity of more than 1.7 m/s, the cleaning degree increases up to 65% and higher. The velocities exceeding 2.5 m/s provide the most complete cleaning of the brush lint from stuck soil.

Conflict of interests: Authors declare no conflicts of interests to disclose.

ACKNOWLEDGEMENTS

This study was financially supported by the Ministry of Science and Higher Education of the Russian Federation and JSC Millerovoselmash. The research results presented in the article were obtained as part of the implementation of the Agreement No. 075-11-2019-041 of November 22, 2019, between the Ministry of Science and Higher Education of the Russian Federation and JSC Millerovoselmash for conducting R&D on the topic “Creating high-tech production of multifunctional complexes for sowing and cultivating row crops and vegetable crops in the system of accurate and zero arable farming based on intelligent mechatronic modules”. The research is performed in the organization of the General Contractor (Federal State Budgetary Educational Institution of Further Professional Education Michurinsk State Agrarian University).

REFERENCES

El Haggar, S (2010). Sustainable Industrial Design and Waste Management Elsevier Netherlands.

Gil, MP, Moya, AMC and Dominguez, ER (2013). Life cycle assessment of the cogeneration processes in the Cuban sugar industry Journal of Cleaner Production Vol 41 Pages 222-231.

Heege, HJ (2013). Precision in Crop Farming: Site Specific Concepts and Sensing Methods: Applications and Results Springer Netherlands Netherlands.

Kleuker, G and Hoffmann, CM (2021). Causes of different tissue strength, changes during storage and effect on the storability of sugar beet genotypes Postharvest Biology and Technology Vol 183 Article 111744 DOI: 10.1016/j.postharvbio.2021.111744.

Kuznetsov, P, Solovyev, S, Gorshenin, V et al. (2020). Reduction of soil layer losses when harvesting sugar beet in the conditions of the central black earth region E3S Web of Conferences Vol 210 Article 04007.

Rajaeifar, MA, Hemayati, SS, Tabatabaei, et al. (2019). A review on beet sugar industry with a focus on implementation of waste-to-energy strategy for power supply Renewable and Sustainable Energy Reviews Vol 103 Pages 423-442 DOI: 10.1016/j.rser.2018.12.056.

Scott, J and Cooke, D (2012). The Sugar Beet Crop Springer Netherlands Netherlands.

Solovyov, SV and Kuznetsov, PN (2016). Theoretical study of the contact interaction of lint with a coil of the spring Bulletin of the Michurin State Agrarian University No 1 Pages 157-161.

Tuğrula, KM, İçöz, I and Perendecic, NA (2012). Determination of soil loss by sugar beet harvesting Soil and Tillage Research Vol 123 Pages 71-77 DOI: 10.1016/j.still.2012.03.012.

Zavrazhnov, AI, Gorshenin, VI, Soloviev, SV, et al. (2019). Resource-saving technology and technology of sugar beet production LAN Saint Petersburg.