¹Department of CSE, DIT University, Dehradun, India

²Department of CSE, DIT University, Dehradun, India

Corresponding author Email: ajayshuk@gmail.com

Article Publishing History

Introduction

Graph coloring is one of the most and frequent studied combinatorial optimization problems in graph theory. A graph G can be defined as pair (V, E) where V is the set of vertices and E is set of edges. The graph coloring problem can be defined as to assign the color to every vertex of the graph by keeping the constraints that no two adjacent vertex have same color and in this process of assigning the color total number of used colors should be minimum. The minimum number of colors that will used to color the vertices of the given graph is called chromatic number of the graph. Graph coloring problem is one of the NP-Hard combinatorial optimization problem which is studied for its complexity associated with computation and for its numerous applications in real world problems. These real world problems mapped into graph coloring problem and solved using a graph coloring algorithm. A few of its applications found in literature are scheduling in different area of applications (Gamache  et al 2007, Zufferey et al 2008), time slots allocation in time table (Werra  1985, Burke  et al 2007), allocation of register (Werra  et al, 1999), assignment of frequency (Smith  et al, 1998), application in communication network (Woo TK et al,2002), Sudoku, pattern matching and applications in parallel computing, (Hao et al, 2017) .

Mostly the algorithms that are used to solve the graph coloring problem can be categorized into two different categories named as approximate algorithms & exact algorithms (Méndez Díaz I. et al,2008, Lucet C. et al ,2006, Méndez-Díaz I,et al 2006, Malaguti E, Monaci M, Toth P, 2011, Segundo PS, 2012). Approximate algorithms includes various techniques to solve the problem such as construction method for register allocation(Chaitin GJ,2004), iterated local search(Caramia M, DellOlmo P,2008), algorithms based on population(Porumbel DC,HaoJK,Kuntz P ,2009, Dowsland KA,Thompson JM ,2008), algorithms based on hybrid approach(Galiner P, Hertz A, Zufferey N,2008) and other  methods based on hybrid local search(Prestwich SD ,2008).

Algorithms available in literature for solving graph coloring problem are mostly approximate in nature due to its hardness and little are exact. For real world applications, the encoding into graph coloring problem is often large and may be not suitable for exact algorithms due to difficulty to solve the large instances after enumeration of search space of the problem.

The constraints in graph coloring problem can be expressed as no two adjacent vertices have same color which is quite simple but this constraint may infer few more constraints among non-neighboring vertices in the graph. The methods available in the literature to deal such problem involves the encoding of the problem using k number of colors into Boolean satisfiability problem and then  algorithm search & explore the additional constraints generated among non-adjoining  vertices by the use of conflict driven clause learning .

In this paper we propose a new algorithm to find the solution for graph coloring problem based on adjacency matrix representation of the given graph for k available colors. In the process of coloring of the vertices in the graph the proposed algorithms that uses only the related to adjacent vertices in the graph and does not generate any additional constraints during coloring process at intermediate stages and thus it avoids any additional constraints to be handled in the process.

Literature Review

In literature there are various techniques available to solve graph coloring problem. In an approach which is based on the conflict driven clause learning with backtracking (Zhaoyang Zhou et al 2014). The approach by the researchers addresses the solution of k-colorability problem with conflict driven clause learning. Researchers have formulated the solution of the problem without encoding the constraints between adjoining vertices in SAT form. Whenever a dead end has encountered algorithm called an implicit constraints generated at intermediate stage. All the constraints searched in this way was represented as CNF clause.

Algorithm1 cdclgcp(G,S,l)

//The input data for the procedure will Graph G, coloing solution set    //S which is partial initially & recursive level l.

// in the graph Kv is set of vailble colors with each vertex v in G.

// The algorithm1 executed initially by calling cdclgcp(G,NULL,0).

// The output will be colour solution set S.

Start :

If( the graph G is NULLL graph  )

return S

Call procedure unitpropagation (G,S,l)

If (kv is empty corresponding to a vertex in the graph or there is a NULL clause)

{

Find the reason R by analysing the conflict.

If (reason is empty)

return NULL

If ( R is non empty)

{

Compute

Implicit constraints =

Implicit constraints  U ( R)

Call procedure backtracking for 2nd largest level(R)

}

Else

return NULL

}

From the graph G choose a vertex v using heuristics

do

{

Delete color C1 from the colorlist of available colors of adjacent vertices of v.

mark the each removal of color C1 as a reason in l+1 level.

S=cdclgcp((Gv,SU(marked reason), l+1)

If (S is not NULL)

return S

Add  C1 to Kv of every adjacent vertex to v

}

while( each color C1 explored in colorlist Kv)

return NULL

End.

The unitpropagation procedure simply discover and generates other unit clauses, unit vertices using propagation. In case the occurrences of conflicts, the reason is analyzed using CNF representation and analyze conflict () procedure.

The algorithms proposed by the researchers is runs in two phases. In the first phase the algorithms search & constructs set of implicit constraints in the graph coloring process and uses it to crop the large search space generated. In the process researchers have applied DSATUR heuristic for the construction of implicit constraints. Next phase of the proposed algorithm constructs the coloring solution set using unit propagation method.

Another approach reported in literature where researchers have tried to give the solution of the graph coloring problem based on genetic algorithm & fuzzy logic (Beigh Tabiya Manzoor et al,2016) . Researchers have defined the following parameters for the optimization in their algorithm

Initial population (used random generation)

1. For selection (used alpha cut based selection)
2. For crossover( used 1- point crossover with probability .8)
3. In mutation phase they have used swapping with probability 0.01

On the basis of above parameters they have proposed the algorithm that runs in the following manner:

Algorithm 2

1. Random initialization of population
2. Evaluation of fitness value
3. Selection of population based parameter defined
4. Applying crossover on resulting population in previous step
5. Apply mutation & replacement operator on data set obtained in previous step.
6. If result obtained is required solution set then exit else goto step 2.

Researchers have proposed above algorithm to solve the problem using optimization techniques based on fuzzy logic & genetic algorithm and tried to give the optimal solution.

Few more techniques have reported in literature in which researchers have proposed the solution by transforming the vertex coloring problem into coupled oscillatory networks (Parihar Abhinav et al, 2018). Another approach is based on graph encoding in the form of adjacency list and researchers have given the solution of the problem with the help of color adjacency list representation of available colors (Shukla, Ajay Narayan et al, 2019). One application area of the problem has been reported in which researchers have tried to address the problem of Device-to-Device communication in wireless networks for improving spectrum utilization and proposed the solution for resource sharing based on graph coloring concept (Tinghan Yang et al, 2017). The other area of applications of the graph coloring problem that has recently reported(Xudong Zhu et al,2017, Mohanad Mohammed Abdulkareem et al ,2017)where application problem has transformed in graph coloring problem to find the solution .

Due to versatile applications of graph coloring problem the methodology used for getting the solution of problem & its complexity is always of the interest of the researchers. A few different approaches to solve the problem based on the types of graphs they have considered for their research problem has discussed in literature (Jaffke L et al, 2017, V.V. Lozin et al, 2017, Petr A. et al, 2016, Arumugam, S et al, 2017).

The graph coloring problem has also addressed for its solution based on cellular learning automaton for getting efficient solution (Rezapoor Mirsaleh, M.  , Meybodi,2016). Graph that is free from induced subgraph another approach may be applied to solve the problem by finding the path & cycles among the given number of vertices (Shenwei Huang, 2016). Another variation of coloring problem is in partition graph coloring problem where with help of optimization technique new results have evolved (Stefka Fidanova, Petrica Pop, 2016). Similarly graph coloring problem has also used to address pricing problem (Morrison David R et al, 2016) and in fuzzy coloring for fuzzy graphs (Samanta, S. et al, 2016) for its efficient solution.

Motivation for Our Approach:

Mostly the solution proposed by researchers have based on explicit constraints of the graph coloring problem along with auxiliary procedure used for handling the other constraints generated during the coloring of vertices in the graph. Some researchers have used learnt clauses management to reduce the search space for coloring by applying certain heuristics. On the other hand some of them have used some other techniques based on genetic algorithm.

In my approach I have devise a new approach that uses only defined constraints for graph coloring problem in the literature and in the coloring process there will be no generation of any additional constraint that required to be handled explicitly. So this approach will reduce the running time for solving the problem.

The proposed approach is based on the representation of given graph in the form of adjacency matrix where the entry in the matrix corresponding to adjacent vertices is 1 otherwise it will 0. Suppose if the given graph is having n number of vertices then it requires to be stored in an nXn square matrix to represent the graph.

In addition to above if there are k number of available colors that will use to assign the colors among the vertices of the graph, we have created additional color matrix of the dimension nXk.

Finally a 1-D array of size n in the algorithm is used to store color that have assigned to every vertices of the graph.

Data Structure Used for The Problem:

 As stated in previous section we present our proposed algorithm matrix representation of the graph, set of available colors and a one dimensional array for storing final color information corresponding to every vertex in the graph.

Suppose given a 3-colorable graph as shown in the figure1 and its adjacency matrix has shown in Table1.

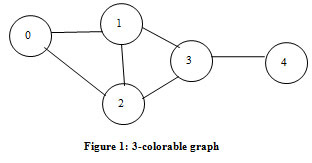Figure 1: 3-colorable graph

Table 1: Adjacency matrix representation of figure 1

	0	1	2	3	4
0	0	1	1	0	0
1	1	0	0	1	0
2	1	0	0	1	0
3	0	1	1	0	1
4	0	0	0	1	0

We have additionally used a color matrix and the matrix representation of available colors for graph can be described as follows:

Table 2: initial color matrix representation for the graph

	0	1	2
0	1	1	1
1	1	1	1
2	1	1	1
3	1	1	1
4	1	1	1

In the above Table 2 the first row of the matrix represents the number of available colors where each color is given a discrete value say for example o represents Red, 1 represent Green and 2 represents Blue color. The first column in figure 3 represents the vertices in the given graph. The values in the color matrix is initially filled with 1 that indicates any color may be assigned to any vertex initially at the starting of the algorithm and in  later stage color matrix will updated as 0 or 1 . The  updation of values in the color matrix will done in the manner that if cm[i][j] is 1 then the jth color may be assigned to vertex i in the graph otherwise it is 0 the jth color cannot assign to vertex i.

Final colors assigned to the vertices of the will stored in the form discrete values into one dimensional array color[].

Proposed Algorithms

In the proposed algorithms we are using adjacency matrix for graph, color matrix, number of available colors and finally assigned color array as global.

Algorithm 3  assigncolor (int i)

{

int i1=i;

for  j=0 to k-1

{

if(cm[i1][j]==1)

{

color[i]=j;

ic=j;              // here ic is global

cm[i][j]=0;

break;

}

}

}

In the above algorithm we are assigning the color to the vertex i that can be obtained from the color matrix after testing the feasibility of assignment of the color in from the execution of for loop.

Algorithm 4  updatecolor( int j)

{

for l=0 to k-1

{

if(cm[j][l]==1&&ic==l)

cm[j][l]=0;

}

}

Above algorithm4 runs to update the values in the color matrix corresponding to those vertices which have previously assigned some color & these values becomes 0 in the color matrix cm[][].

Algorithm 5  GCP Color( )

{

for i=0 to n-1

{

assigncolor(i);

for j=i+1 to n-1

if(a[i][j]==1)

updatecolor(j);

}

Initially algorithm 5 will call algorithm3 to assign the color to vertices of the graph .Once color has assigned to a particular vertex in the graph , calls algorithm 4 to update the color matrix.

Working of Proposed Algorithm & its Analysis

Before starting of the algorithm we are assuming that the given graph has stored in the form of adjacency matrix a[][] where entry if a[i][j] is 1 then vertex j is adjacent vertex to i otherwise if it is 0 j is a non-adjacent vertex to i. Similarly color matrix cm[][] is initially assigned as 1 for its every value and it has been updated in algorithm4 .

We have executed above proposed algorithm on several graphs and found it will always terminated by assigning the colors to the vertices of the work in the form of exact algorithm that is it will uses the minimum colors to color the graph.

Suppose the algorithm runs on the given graph in figure 1 after the assigning the colors to the vertices say 0 the content of color matrix (Table 3) and color assignment array (Table 4) will as follows:

Table 3: content of color matrix after assigning vertex 0 as Red.

	0	1	2
0	0	1	1
1	0	1	1
2	0	1	1
3	1	1	1
4	1	1	1

Table 4: color array after assigning color Red (0) to vertex 0 in the graph

0

Analysis of proposed algorithm

The formal analysis of the proposed algorithms is simple. We have implemented the proposed algorithm on windows based Turbo C although it can be implemented on any platform without affecting its complexity. Suppose the number of vertices in the given graph is n and total number of available colors is k. The formal analysis of algorithms proposed may be done in the following manner:

• The procedure assigncolor( ) will called n times which in turns executes maximum k times for every calling so the total number of execution time will be( n*k )times.
• The procedure updatecolor( ) will called n-1 times for its every calls by GCPColor and in this case the total number of calls of procedure updatecolor( ) will be (n*(n-1)) times.
• The instructions in procedure updatecolor( ) itself executed maximum k times in every call.
• So the total number of times instructions executed in procedure updatecolor( ) will be (n*(n-1)*k)

Finally the total number of instructions executed in the proposed algorithm will be (n*k)+(n*n-1*k).It is therefore complexity of the proposed algorithm will be O( n*(n-1)*k).

Conclusion & Future Scope

In the proposed research work we tried to give the solution for graph colouring problem with the help of traditional data structure available in the literature by adopting a completely new approach. Although the solution for the problem available in the literature in the form of either approximate or exact algorithm but every approach have its own flaw. In some cases algorithms will work for dense graph but fails to work satisfactory in case sparse graph. In our case the proposed approach will work with same capability in any kind of graph without affecting its complexity.

Since the graph coloring problem is a NP class problem, so there will be always possibility of improving the running time of algorithm and this may be improved by either changing the data structure that reduces the complexity for the searching the adjacent vertices for updating the color list corresponding to each vertex in the graph or by use of certain heuristics that reduces the search space updating the color matrix.

References

Gamache M, Hertz A,Ouellet JO. “A graph coloring model for a feasibility problem in monthly crew scheduling with preferential bidding”. In Comput Oper Res 2007;34(8): 2384–95.

Zufferey N, Amstutz P, Giaccari P. “Graph coloring approaches for a satellite range scheduling problem”. In J Schedul 2008;11(4):263–77.

Werra DD. “An introduction to time tabling”. In Eur J Oper Res1985;19:151–62.

Burke EK, McCollum B, Meisels A, Petrovic S, Qu R. “A graph based hyper heuristic for time tabling problems”. In EurJOperRes2007;176:177–92.

Werra D D, Eisenbeis C, Lelait S, Marmol B. “On a graph theoretical model for cyclic register allocation”. In Discret Appl Math1999;93(2–3):191–203.

Smith DH, Hurley S, Thiel SU. “Improving heuristics for the frequency assignment problem”. In Eur JOper Res1998;107(1):76–86.

WooTK,Su.SYW,WolfeRN. Resource allocation in a dynamically partionable bus network using a graph coloring Algorithm. IEEE Trans Commun 2002, 39: 1794-801.

Hao et al. Algorithms for balanced graph coloring with applications in parallel computing IEEE Transactions on Parallel & Distributed Systems 2017 28(1):

Méndez Díaz I, Zabala P. “A cutting plane algorithm for graph coloring”. In Discret Appl Math 2008;156(2):159–79.

Lucet C, Mendes F, Moukrim A. “An exact method for graph coloring”. In Comput Oper Res 2006;33(8):2189–207.

Méndez-Díaz I, Zabala P. “A branch-and cut algorithm for graph coloring”. In Discret Appl Math 2006;154:826–47.

Malaguti E, Monaci M, Toth P. “An exact approach for the Vertex Coloring Problem”. In Discrete Optim 2011;8(2):174–90.

Segundo PS. “A new DSATUR based algorithm for exact vertex coloring”. In Comput Oper Res 2012;39:1724–33

Chaitin GJ. “Register allocation and spilling via graph coloring”. In SIGPLAN Not 2004;39(4):66–74.

Caramia M, DellOlmo P. “Coloring graphs by iterated local search traversing feasible and infeasible solutions”. In Discret Appl Math 2008;156(2):201–17.

Porumbel DC,HaoJK,Kuntz P. Diversity control and multi parent recombination for evolutionary graph coloring algorithms.In:9^th European conference on evolutionary computation in combinatorial optimization (EVOCOP2009). Tbingen, Germany; 2009.p.121–32.

Dowsland KA,Thompson JM. An improved ant colony optimization heuristic for graph coloring DiscretApplMath2008;156(3):313–24.

Galiner P, Hertz A, Zufferey N. An adaptive memory algorithm for the k-coloring problem. Discret Appl Math 2008, 156(2):267-79.

Generalized graph coloring by a hybrid of local search and constraint programming. Discret Appl Math 2008, 156(2):148-58

Zhaoyang Zhou, Chu-Min Li, Chong Huang, Ruchu Xu An exact algorithm with learning for the graph coloring problem Computers & Operation Research 51(2014)282-301.

Tabiya Manzoor Beigh,Girdhar Gopal. Use of Genetic Algorithm and Fuzzy Logic in Optimizing Graph Coloring Problem IJCA Proceedings on Recent Innovations in Computer Science and Information Technology RICSIT 2016(1):1-4

Abhinav Parihar et al. Vertex coloring of graphs via phase dynamics of coupled oscillatory networks. Scientific Reports, 7:11, DOI: 10.1038/s41598-017-00825-1.

Shukla ,Ajay Narayan ,Garg M.L., Misra,Rajiv . An Approach to Solve Graph Coloring Problem using Linked List, International Journal of Advanced Studies of Scientific Research ,Vol 4,No. 2 ,2019.

Tinghan Yang, Rongqing Zhang, Xiang Cheng, Liuqing Yang, Graph Coloring Based Resource Sharing (GCRS) Scheme for D2D Communications Underlying Full-Duplex Cellular Networks.IEEE Trans on Vehicular Technology 2017 , 66(8):7506-7517.

Xudong Zhu ,Linglong Dai, Zhaocheng Wang, Xiaodang Wang. Weighted-Graph-Coloring-Based Pilot Decontamination for Multicell Massive MIMO Systems. .IEEE Trans on Vehicular Technology 2017, 66(3):2829-2834.

Mohanad Mohammed Abdulkareem, Shadha Adnan Yaseen, Labeeb Mohsin Abdullah. Matrix based graph coloring algorithm for LTE-PCI assignment and reassignment reduction. 2017 IEEE 8th Control and System Graduate Research Colloquium (ICSGRC), DOI, 1109/ICSGRC.2017.8070565.

Jaffke L., Jansen B.M.P. (2017) Fine-Grained Parameterized Complexity Analysis of Graph Coloring Problems. In: Fotakis D., Pagourtzis A., Paschos V. (eds) Algorithms and Complexity. CIAC 2017. Lecture Notes in Computer Science, vol 10236. Springer, Cham.

V. Lozin,D.S. Malyshev. Vertex coloring of graphs with few obstructions. Discret Appl Math 2017, 216(1):273-280.

Petr A. Golovach, Matthew Johnson, Daniël Paulusma, Jian Song.

A Survey on the Computational Complexity of Coloring Graphs with Forbidden Subgraphs. Journal of Graph Theory 2016, Wiley Perodicals,Inc.

Arumugam, S., Premalatha, K., Bača, M. et al. Local Antimagic Vertex Coloring of a Graph. Graphs and Combinatorics (2017) 33: 275.

Rezapoor Mirsaleh, M. & Meybodi.,A new memetic algorithm based on cellular learning automata for solving the vertex coloring problem . R. Memetic Comp. (2016) 8(3):211-22.

Shenwei Huang. Improved complexity results on k-coloring P_t –free graphs, European Journal of Combinatroics ,2016,(51): 336-346.

Stefka Fidanova, Petrica Pop. An improved hybrid ant-local search algorithm for the partition graph coloring problem. Journal of Computational and Applied Mathematics, 2016, (293): 55-61.

David R. Morrison, Edward C. Sewell, Sheldon H. Jacobson.

Solving the Pricing Problem in a Branch-and-Price Algorithm for Graph Coloring Using Zero-Suppressed Binary Decision Diagrams. INFORMs Journal on Computing 2016, 28(1):67-82.

Samanta, S., Pramanik, T. & Pal, M.Fuzzy colouring of fuzzy graphs Afr. Mat. (2016) 27: 37-50.