Comparison of accuracy of Epsilon and Quadratic

loss function for predicting saturated hydraulic

conductivity by SVR and SVR-GA models

Masoume Mehmandoust

, Jaber Soltani

, Mahmood Mashal

, Moosa Kalanaki

Rahim Sadeghifar

and Tohid Asadollahzade

1,6

Postgraduate student, Department of Irrigation and Drainage Engineering, College Of Abureyhan, University

of Tehran, Iran

Assistant Professor, Department of Irrigation & Drainage Engineering, College Of Abureyhan, University of

Tehran, Iran

Associate Professor, Department of Irrigation & Drainage Engineering, College Of Abureyhan, University of

Tehran, Iran

Postgraduate student, Department of Arti cial Intelligence, Rouzbahan Higher Education Institute Sari, Iran

Postgraduate student, Department of Irrigation and Drainage Engineering, Lecturer, Higher Education Center

of Imam Khomeini, Iran

ABSTRACT

Saturated hydraulic conductivity is one of the most effective hydraulic characteristics of the soil processes. One of the

methods to measure saturated hydraulic conductivity above water table is applying cased boreholes. Support vector

machine is a classi er which uses statistical train theory for classi cation and regression; and genetic algorithm is

a searching technique in optimization problems inspired from the nature and the evolution of the creatures. In this

research Epsilon and quadratic loss functions are compared against each other in support vector machine model

(SVR) and support vector machine-genetic algorithm model (SVR-GA). These models are developed by the core radial

function to predict the saturated hydraulic conductivity to be a suitable replacement for Reynolds analytical solutions

in cased boreholes. The data used in this study are consisting of soil moisture percentage, saturated soil moisture

percentage, the water table fall versus time, time, size of boreholes and the quantities of saturated hydraulic conduc-

tivity of the soil calculated by Reynolds solution. 70 percent of data is used for the train, 20 percent for the test and

10 percent for the validity. In order to analyze the results we have used three different statistical indicators including

correlation coef cient (R2), root mean square error (RSME), and normalized root mean square error (NRMSE). Accord-

ARTICLE INFORMATION:

*Corresponding Author: jsoltani@ut.ac.ir

Received 27

Nov, 2016

Accepted after revision 2

March, 2017

BBRC Print ISSN: 0974-6455

Online ISSN: 2321-4007

Thomson Reuters ISI ESC and Crossref Indexed Journal

NAAS Journal Score 2017: 4.31 Cosmos IF : 4.006

reserved.

Online Contents Available at: http//www.bbrc.in/

Biosci. Biotech. Res. Comm. Special Issue No 1:94-101 (2017)

Masoume Mehmandoust et al.

ing to the results of SVR-GA model in all three types of  ow the coef cient of determination was above 0.99 and

root mean square error and mean absolute error were less than 0.02. The results of this research indicate that Epsilon

loss function had better accuracy than quadratic loss function but in terms of execution time quadratic loss function

is considerably more ef cient than Epsilon loss function.

KEY WORDS: GENETIC ALGORITHM, LOSS FUNCTION, SUPPORT VECTOR MACHINE, SATURATED HYDRAULIC CONDUCTIVITY

INTRODUCTION

Although the equations calculating hydraulic conduc-

tivity of soil which are including a variety of hydrau-

lic processes are quite accurate but they include a lot

of computational stages. On one hand adding different

aspects of processes within these equation has increased

their accuracy, but it has enhanced the computational

load as well. One of the methods to confront increas-

ing computational load is using a meta-model. In other

words developing an alternative model instead of the

main model which has learnt the relations based on

input and output can be more effective in computa-

tional ef ciency. Applying the appropriate solutions

to increase the accuracy of approximated models and

ef cient use of them can be known as alternative

meta-model management. Nowadays the topic of alter-

native model management has been known as a new

 eld of research and has attracted a lot of attention

to it.

Saturated hydraulic conductivity is one of the most

effective hydraulic characteristics affecting the soil pro-

cesses (Reynolds and Topp, 2008). These parameters

play a fundamental role in controlling the hydrological

processes of underground  ows (Reynolds and Elrick,

2005). In order to measure saturated hydraulic conduc-

tivity of soil different methods are available according

to the soil type and the difference between the levels

of underground water wit surface. One of the methods

of measuring hydraulic conductivity is borehole method

which in known as the falling head lined boreholes per-

meameter method (Navin et al. 2008). Philip has pre-

sented an approximately analytical solution for this type

of borehole. Philip borehole only studies vertical  ows.

In the following, Reynolds studied different geome-

tries of  ow and various radiuses of tanks and Philip’s

borehole as well and analyzed them. Due to the high

volume of computing in these analyses we can use an

alternative model which has been developed by arti cial

intelligence in order to predict saturated hydraulic con-

ductivity of soil. Arti cial intelligence (AI) models has

been used in a wide range of  elds. AI models are quick,

robust, and convenient to use for the prediction and

solving complex problems compared with conventional

methods which impose more dif culties, time consump-

tion, and high expenses.

Shams Emamzadeh et al, (2017) in a study has com-

pared the performance of Multi-Layer Perceptron (MLP)

and Radial Basis Function (RBF) in neural networks for

estimation of the soil saturated hydraulic conductivity.

Amongst the AI models with high accuracy are support

vector machine model (SVR) and genetic algorithm- sup-

port vector machine combined model (SVR-GA). In this

study the prediction of saturated hydraulic conductivity

of soil via SVM and SVM-GA model has been calculated

using soil moisture percentage, saturated soil moisture

percentage, the water table fall versus time, time, and

size of the boreholes and the values of saturated hydrau-

lic conductivity of soil calculated by Reynolds solution

(Mehmandoust, 2014).

SVM is a collection of training techniques by the

machine which is used for classi cation and or regres-

sion and is introduced based on statistical train theory

and minimization of loss probability (Kalanaki and Sol-

tani, 2013a; Vapnic, 2010). Genetic algorithm (GA) is a

metaheuristic also one of the numerical optimization

algorithms which is inspired from the nature and is a

good option for the models use regression for prediction.

These algorithms are by relying on bio-inspired opera-

tors such as crossover, mutation and natural selection.

SVM has better ef ciency comparing neural networks

for  ood probability prediction (Liong and Sivapra-

gasam, 2000). Yang Shao and Huang Yuan Fang (Yang

and Huang, 2007) used SVM model in order to predict

the parameters of hydraulic characteristics of soil and

concluded that there was no obvious difference between

the predicted results and the observed ones. Navin

Twarakawi et al (Navin et al. 2008) used SVM model to

estimate hydraulic parameters of soil, in this study all

the parameters which were estimated based on transfer

function and via SVM model showed better reliability

compared with ROSETTA PTF program.

Kalanaki et al. (2013) conducted a comparative study

about different Kernel functions and loss functions

in support vector machine using SVM_GA combined

model in order to predict the refraction rate of the pipes

in water distribution network. The  ndings of this study

showed the better ef ciency of radial Kernel functions

and quadratic loss functions. Krzysztof Lamorski et al

(Lamorski et al. 2011) modelled soil water retention using

SVM with the optimized model of genetic algorithm. The

 ndings of the study showed that suing SVM model with

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS COMPARISON OF ACCURACY OF EPSILON AND QUADRATIC LOSS FUNCTION 95

Masoume Mehmandoust et al.

the optimized genetic algorithm for soil water retention

modelling is better than the prior tested methods. Chen

Hai Yan et al (Chen et al. 2011) used SVR-GA model to

predict aquifer hydraulic conductivity and water surface

table computation. The  ndings of their study proved

that the model had performed accurate in predicting

hydraulic conductivity.

This research aims at assessing and comparing regres-

sion support vector machine and hybrid model of genetic

algorithm and regression support vector machine (SVR-

GA) by Epsilon and quadratic loss functions with the

help of the prior study’s  ndings (Asadollah Zade, 2013)

which apply Reynolds and Philip methods to predict

hydraulic conductivity of soil; and also with develop-

ing an arti cial intelligence model  nds an alternative

model for analytical Reynolds model which involves a

great deal of computational processes.

MATERIALS AND METHODS

One of the methods of measuring hydraulic conductivity

is using boreholes which is known as the falling-head

lined boreholes permeameter method (Philip, 1993).

The method uses cased boreholes and gives saturated

hydraulic conductivity based on the drop in levels of

water versus time. In Philip Solution, the walls of the

borehole are all covered and permeation occurs only

from the  oor and vertical. In Reynolds method, the

most common and probable types of  ow geometry and

various radii of tanks for permeameter of boreholes are

taken into consideration which consist of: only vertical

 ow (Philip), only radial  ow (permeable wall with the

length L and impermeable  oor) and a combination of

vertical and radial  ows where the permeable section

has the length L and the radius a. The data used in the

model were collected from 27 drilled boreholes in 1 in 1

meter grid with 3 repetitions and for three types of  ow

including vertical, horizontal and vertical-horizontal

 ows (radial). Plastic pipes were used to cover the walls

of the borehole and the size of the boreholes included

three diameter 4, 6 and 8 cm with different lengths (Asa-

dollah Zade, 2013).

HYDRAULIC CONDUCTIVITY

Saturated hydraulic conductivity values used in the

models are obtained from Reynolds’ approximate ana-

lytical solution. These solutions include many equations

and long computational steps which require input data

such as soil moisture percentage, saturated soil mois-

ture percentage, drop in water levels versus time, time,

borehole’s size including the borehole’s radius and the

covered length as well as uncovered length in different

considered geometries.

SUPPORT VECTOR MACHINE

Support vector machine is a collection of train meth-

ods by machine which is used for classi cation and

regression and is based on statistical train theory and

loss probability minimization (Shams Emamzadeh et

al. 2017; Vapnic, 1995; Kalanaki et al. 2013). The func-

tion that is used to calculate regression support vector

machine is in the form of mapping from the input space

of Xi to output space of Yi and is represented by equa-

tion (Asadollah Zade, 2013):

(1)

Where W and b represent weight and bias respectively. In

regression support vector machine the aim is estimating

b and W in order to achieve the best results. In regression

support vector machine represents the difference between

the actual data and the results data and the variable rep-

resents an allowed extent of error that can occur by vari-

ous factors such as noise (Kalanaki et al. 2013; Smola and

Scholkopf, 1998). Margin is de ned as the ration of and

to maximize margin we should minimize. These stages are

considered in equations (2) and (3) which are the building

blocks of regression support vector machine (Simunek et

al. 2006; Lamorski et al. 2011):

(2)

Subject to:

(3)

C determines an exchange between the size of margin

and the extent of error in train and controls over- tting

in train. We use Kernel functions because working with

above functions can be costly and time-consuming. Ker-

nel function is a linear classi er based on dot product

of vectors which is equal to k Kernel function is equiva-

lent to the inner product in the feature space. There-

fore, instead of costly calculations in feature space we

apply Kernel function. Here W is obtained from equation

(Kalanaki and Soltani, 2013a). Finally, the regression

support vector machine with the effect of Kernel func-

tions is obtained from equation (Kalanaki and Soltani,

2013a):

(4)

(5)

96 COMPARISON OF ACCURACY OF EPSILON AND QUADRATIC LOSS FUNCTION BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Masoume Mehmandoust et al.

One of the most useful basis-functions is Gaussian basis

function or radial basis function (RBF) which is shown

in equation (Lamorski et al. 2011):

(6)

Where Xi and Xj are support vectors and is the band-

width of the radial basis Kernel function. To minimize

the error and other risks we aim at  nding a function

which is shown in equation (Liong and Sivapragasam,

2000):

(7)

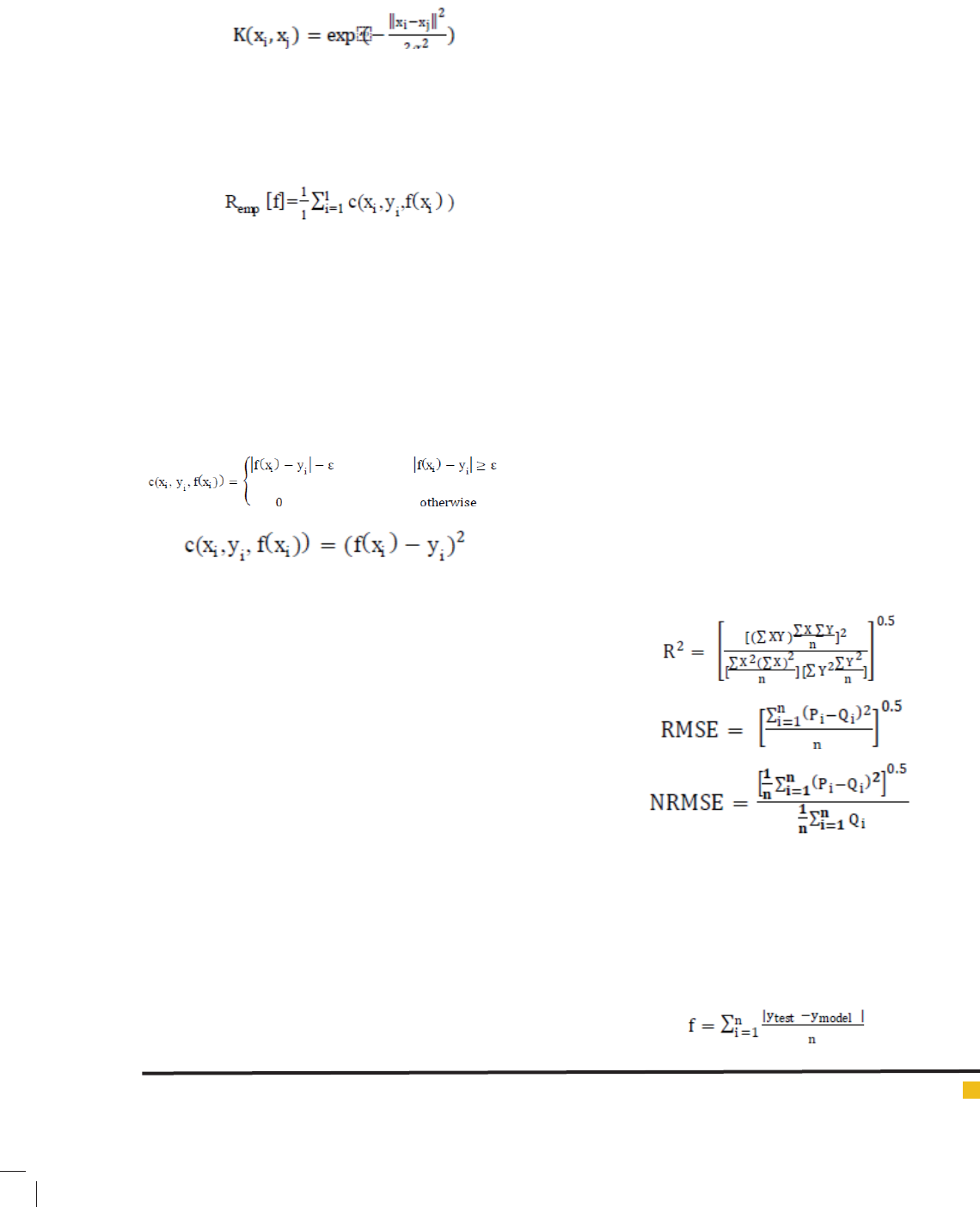
Function refers to cost function and indicates the pen-

alty for estimate function according to experimental

data. Remp represents the experimental error. Loss func-

tion determines the penalty of data while estimating. In

this study two types of loss functions are utilized which

are Epsilon loss function and quadratic loss function.

Figure (1) shows the diagrams of these functions.

The values of epsilon and quadratic loss functions are

obtained respectively by equations (8) and (9):

(8)

(9)

GENETIC ALGORITHM

Genetic algorithm was introduced by John Holland

according to evolution theory of Darwin in the early

1970s. The optimization search procedure in genetic

algorithm is based on a guided random procedure. The

procedure has been inspired from the nature and the

evolution of living creatures. In this method each mem-

ber of the population is shown through a string com-

posed of variables where each variable is called gene and

the string composed of genes is called chromosome. In

fact, initially for a number of responses which is called

population a set of objective parameters are generated

randomly. After running numerical simulator program

which represents the  tness of the set of data, a  tness

value will be attributed to the member of the population.

This will repeat for each and every developed member,

after calling genetic algorithm operators such as crosso-

ver, mutation and selection operators and while retain-

ing the top part of the population, the next generation

will be formed and this procedure will continue till one

of the stop conditions is satis ed. At the end, the mem-

ber of the population that has the best  tness value will

be selected (Kalanaki and Soltani, 2013a; Kalanaki and

Soltani, 2013b).

MODEL DEVELOPMENT

The studies conducted in this research are carried out in

the research  eld of Abureyhan campus of Tehran Uni-

versity which is located in Pakdasht. In order to develop

and run SVR model we need to adjust the parameters

c,  and  in the models engaging Epsilon loss func-

tion and the parameters c and  must be modi ed in

the models involving quadratic loss function. In order

to  nd the most suitable combination of this parameters

in SVR model, trial and error method must be used and

the combination with the least amount of error and the

highest correlation must be selected. It can be mentioned

that one of the downfalls of SVR model is  nding such

a combination using trial and error method. In order to

 nd the best combination GA optimization model was

applied. The model was developed and implemented for

three kinds of  ows introducing input data matrixes

which were composed of the combinations of applied

variables in Richards and Van Genuchten-Maulem equa-

tions and the dimensions of the boreholes and output

matrix including the values of hydraulic conductivity

calculated by HYDRUS, Kernel and the desired loss func-

tion selection and introducing the optimal parameters

and the values of correlation coef cient, root mean

square error and normalized root mean square error

were calculated. Equations (10) to (12) show these rela-

tions respectively:

(10)

(11)

(12)

Where Pi represents the estimated or stimulated value,

Qi is the observed value and n is the number of samples.

In developing GA, the number of the initial popu-

lation was 20, the combination type was single point,

selection rate was 0.5, mutation rate was 0.25 and the

number of replications was considered 300. Equation

(13) represents the  tness function in genetic algorithm.

(13)

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS COMPARISON OF ACCURACY OF EPSILON AND QUADRATIC LOSS FUNCTION 97

Masoume Mehmandoust et al.

In the equation above, f represents the average of errors,

n is the number of test’s data, ytest is the experimental

values and y model is the estimated values. Genetic algo-

rithm using a variety of different parameters’ combina-

tions converges to a certain extent of error in desired

replications. In this study after normalization in order

to use Kernel function, 70 percent of data were used for

train, 20 percent for test and 10 percent for validation.

In order to write and run the codes we have used MAT-

LAB software.

The optimal parameters achieved by the hybrid model

were used in Support Vector Machine. Set of chromo-

somes make up the population. The encoding process of

each chromosome in the consolidated SVR-GA model

includes , C and. A set of chromosomes make up the

population (Kalanaki et al, 2013; Kalanaki and Sol-

tani, 2013a; Kalanaki and Soltani, 2013b; Smola and

Scholkopf, 1998; Shams Emamzadeh et al. 2017; Vapnic,

1995; Vapnic, 2010; Yang and Huang, 2007).

RESULTS AND D ISCUSSION

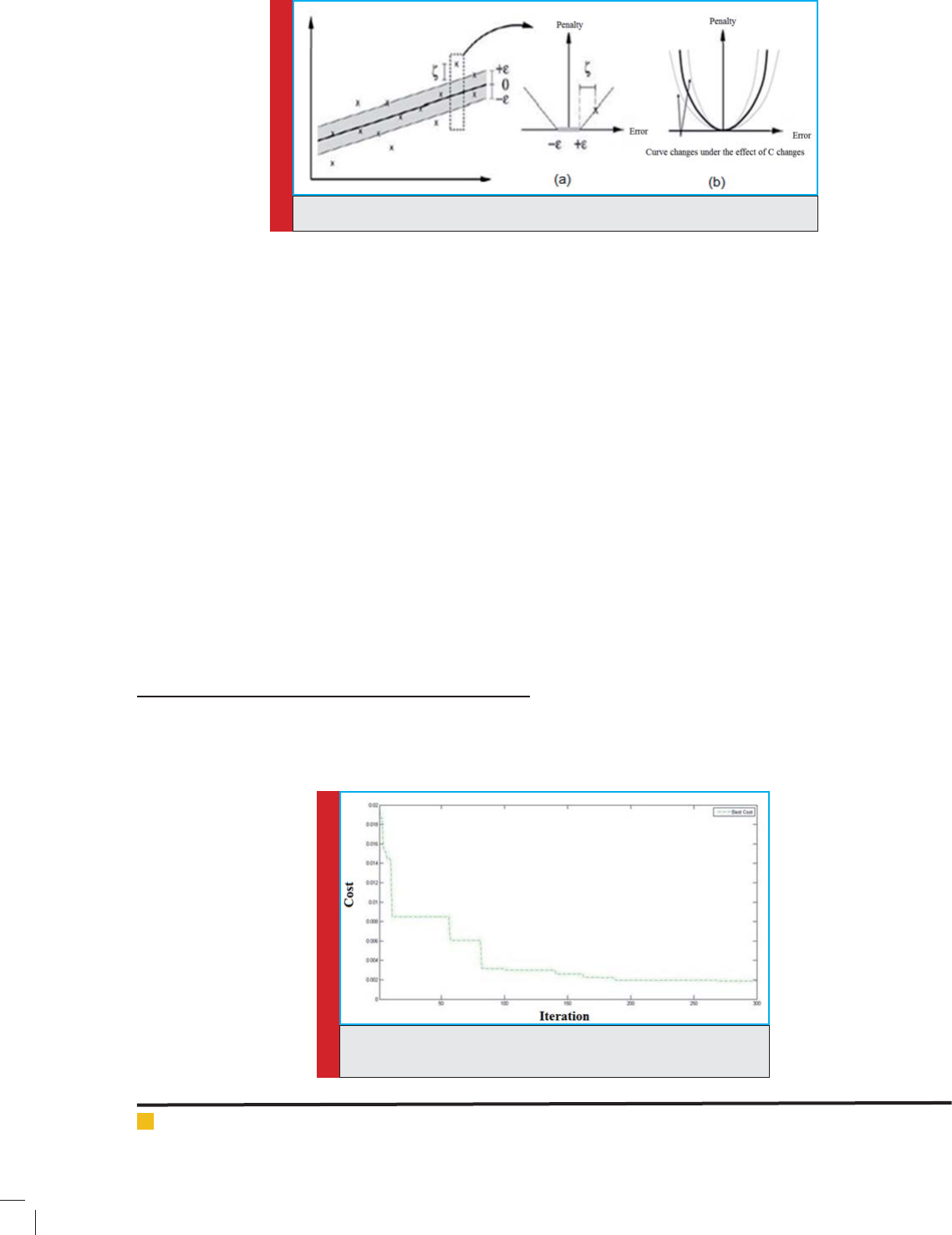
The diagram shown in  gure 2 represents the conver-

gence of the objective function of genetic algorithm in a

horizontal  ow at an Epsilon loss function.

The results of the SVR and SVR-GA models with

radial Kernel function at Epsilon loss functions are rep-

resented in table 1 in three different  ows including

horizontal, vertical and vertical-horizontal.

The results of the SVR and SVR-GA models with

radial Kernel function for quadratic loss functions

are represented in table 2 in three different  ows

including

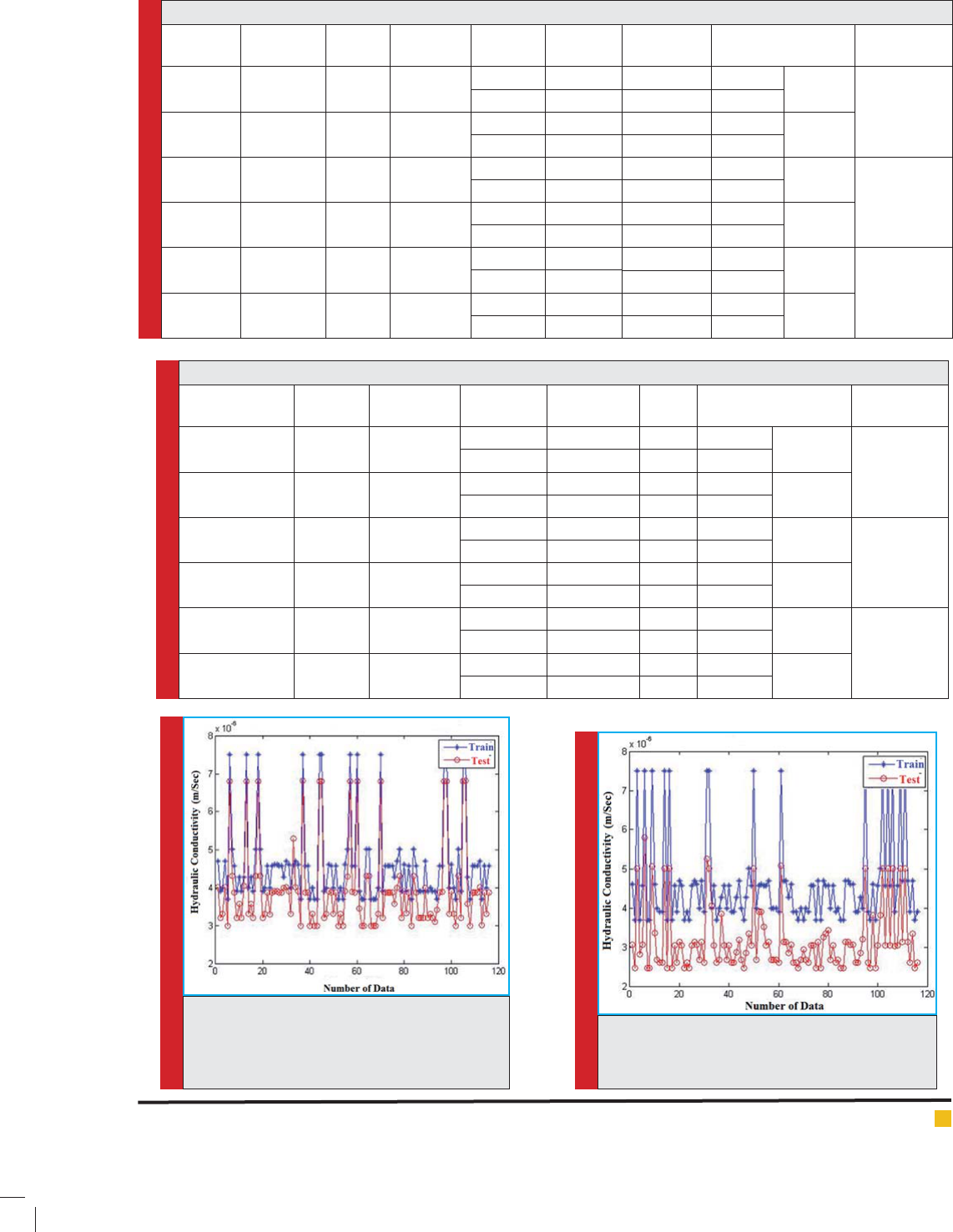
Figures 3 and 4 represent the diagrams regarding the

prediction of hydraulic conductivity by using of SVR

model with test and train data for Epsilon and quadratic

loss functions in horizontal  ows respectively. The lon-

gitudinal axis shows the number data and the transverse

axis shows the values of hydraulic conductivity.

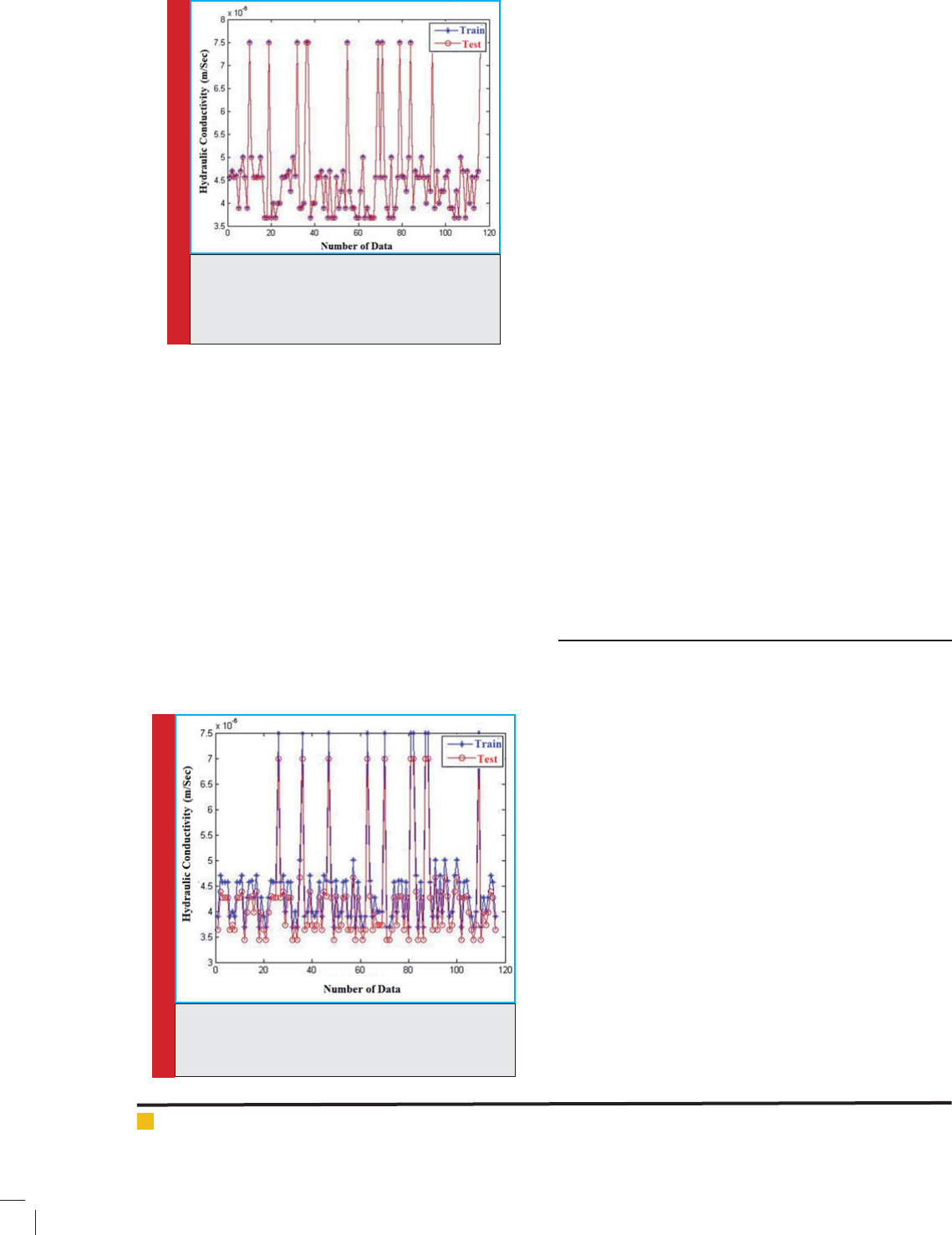
Figures 5 and 6 represent the diagrams regarding the

prediction of hydraulic conductivity by using of SVR-

GA model with train and test data for Epsilon and quad-

ratic loss functions in horizontal  ows respectively. The

longitudinal axis shows the number data and the trans-

verse axis shows the values of hydraulic conductivity.

As it can be seen in table-1 SVR model has accurate

and desirable results for three different types of  ows

(high correlation coef cient and low levels of error)

and SVR-GA model also has excellent results (correla-

tion coef cients close to 1 and error percentage close to

zero). In SVR model of all three different  ows determi-

FIGURE 1. (a) Epsilon loss function (b) Quadratic loss function

FIGURE 2. The convergence of GA in horizontal  ow at epsilon

loss function

98 COMPARISON OF ACCURACY OF EPSILON AND QUADRATIC LOSS FUNCTION BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Masoume Mehmandoust et al.

Table 1. The results of SVR and SVR-GA for epsilon loss function

Flow typeModel typeR2 (%)

RMSE

(m.s-1)

NRMSE





Run-time

(seconds)

Horizontal

 ow

SVR

prediction9786219/009244/019474/0

0004/0700000019/097922

validity9591991/013031/019018/0

SVR-GA

prediction9999973/000089/000175/0

00021049/05665/7200000791/093021

validity9999955/000117/000169/0

Horizontal-

vertical  ow

SVR

prediction9897919/006601/015938/0

0004/090000004/092131

validity9780319/009329/017917/0

SVR-GA

prediction9999997/000033/000292/0

00001433/01760/4800003758/090456

validity9999998/000025/000173/0

Vertical  ow

SVR

prediction9492773/011536/016723/0

00003/01100007/0103985

validity9356536/012313/016578/0

SVR-GA

prediction9994702/000995/001309/0

00001598/05493/4000002245/094783

validity9991326/001095/001271/0

Table 2. The results of SVR and SVR-GA for quadratic loss function

Flow typeModel type

(%)

RMSE

(m.s-1)

NRMSE



Run-time

(seconds)

Horizontal

 ow

SVR

prediction9248/019230/045416/0

0007/03029217

validity9269/019246/046718/0

SVR-GA

prediction9973/003494/007426/0

00029126/03766/15523699

validity9989/002133/006967/0

Horizontal-

vertical  ow

SVR

prediction9462/017164/039274/0

00075/08527660

validity9424/018326/034866/0

SVR-GA

prediction9991/002105/005838/0

00021562/01387/13221518

validity9985/002385/008277/0

Vertical  ow

SVR

prediction8506/019525/027422/0

0005/016032223

validity8459/016398/026374/0

SVR-GA

prediction9782/006917/009189/0

00004794/09392/24628416

validity9977/002049/008563/0

FIGURE 3. The prediction of hydraulic conduc-

tivity with test and train data by using of SVR

model, with epsilon loss function in horizontal

 ow

FIGURE 4. The prediction of hydraulic conductivity

with test and train data by using of SVR model,

with quadratic loss function in horizontal  ow

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS COMPARISON OF ACCURACY OF EPSILON AND QUADRATIC LOSS FUNCTION 99

Masoume Mehmandoust et al.

nation coef cient is above 0.93 and root mean square

error and mean absolute error are less than 0.2; in the

event that SVR-GA model of all the  ows determination

coef cient is more than 0.99 and root mean square error

and mean absolute error is less than 0.02. Thus, hybrid

model with epsilon loss function is apparently more ef -

cient. This superiority is shown in Figure 5.

According to the results seen in table 2 for SVR model

does not contain good results for quadratic loss function

but SVR-GA model shows very desirable results. In SVR

model for all three  ows, determination coef cient is

more than 0.84 and root mean square error and mean

absolute error are less than 0.47; in SVR-GA model for

all three  ows determination coef cient is above 0.97

FIGURE 5. The prediction of hydraulic con-

ductivity with test and train data by using of

SVR-GA model, with epsilon loss function in

horizontal  ow

FIGURE 6. The prediction of hydraulic conductivity

with test and train data by using of SVR-GA model,

with quadratic loss function in horizontal  ow

and root means square error and mean absolute error

are below 0.1. Therefore, hybrid model is much more

ef cient as it can be observed. The results obtained from

epsilon loss function are more accurate as compared

to the results gained from quadratic loss function. The

results are demonstrated graphically in  gure 6. In both

models the results obtained from epsilon loss function

were more precise. This procedure is obvious in diagram

3 to 6. But the considerable point is the execution time

for epsilon loss function in both models is quite insig-

ni cant. According to the  ndings it can be declared

that model hybrid model with epsilon loss function

is an appropriate alternative for analytical Reynolds

solutions.

Eventually, Results show that epsilon function accu-

racy is better than the quadratic function, but in terms of

run time, quadratic function is superior to epsilon func-

tion signi cantly. Results show that accuracy of epsilon

function is better than the quadratic function. Hybrid

model with the epsilon loss function is superior. For

quadratic loss function, the results of SVR model are not

acceptable but SVR-GA model have a very good results.

According to the results, we can say that a hybrid model

with epsilon loss function very good alternative for the

Reynolds analytical solution. The results of epsilon loss

function in both models have higher accuracy in com-

parison with the quadratic loss function, but in terms of

run time, quadratic function is superior to epsilon func-

tion signi cantly.

ACKNOWLEDGEMENTS

This article is extracted from the thesis of Masoume

Mehmandoust, University of Tehran. The authors appre-

ciate from University of Tehran for their support.

REFERENCES

Asadollah Zade, T., (2013): Measurement of saturated hydrau-

lic conductivity and absorption number with methods of bore-

hole permeameter and assessment of this methods by Hydrus

2D model, master thesis, Irrigation and drainage engineering,

College of Abouraihan, Tehran university, 129 pages, in Per-

sian with English abstract.

Chen, H. and Y.Teng and J. WANG, (2011): Method of estima-

tion of hydraulic conductivity with genetic algorithm-support

vector regression machine. China Academic Journal Electronic

Publishing House. 5 pages.

Kalanaki, M. and J. Soltani, (2013a): Performance assessment

among hybrid algorithms in tuning SVR parameters to predict

pipe failure rates, Advances in Computer Science: an Interna-

tional Journal, Vol. 2, Issue 5, 7 pages.

Kalanaki, M. and J. Soltani, (2013b): Simulation and Perfor-

mance Assessment between hybrid algorithms SVR-CACO and

100 COMPARISON OF ACCURACY OF EPSILON AND QUADRATIC LOSS FUNCTION BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Masoume Mehmandoust et al.

SVR-CGA to more accurate predicting of the pipe failure rates.

Journal of Novel Applied Sciences, 2(S3): 1054-1063, 10 pages.

Kalanaki, M., j. Soltani and S. Tavassoli, (2013): Management

of urban water infrastructure systems by prediction of rate of

pipe failure by using of SVR-CGA hybrid model, Twelfth Con-

ference of hydraulic of Iran, 8 pages, in Persian with English

abstract.

Lamorski, K., C. Sławin

ski, F. Moreno, G. Barna, W. Skierucha

and J. L. Arrue, (2011): Modelling soil water retention using

Support Vector Machines with genetic algorithm optimization,

The Scienti c World Journal, Volume2014(2014), 10 pages.

Liong, S.Y., and C. Sivapragasam. (2000): Flood stage forecast-

ing with SVM. J. Am. Water Resour. Assoc. 13 pages.

Mehmandoust, M., (2014): Evaluation of saturated hydraulic

conductivity prediction using a hybrid model of genetic algo-

rithm and support vector machine. Msc. Thesis, Department of

Irrigation and Drainage Engineering, Collage of Abouraihan,

University ofTehran.

Navin K. C. Twarakavi, J Simunek and M. G. Schaap, (2008):

Development of Pedotransfer Functions for Estimation of Soil

Hydraulic Parameters using Support Vector Machines. Soil Sci-

ence Society of America, 10 pages.

Philip, J.R. (1993): Approximate analysis of falling-head lined

borehole permeameter. Water Resour. Res. 29:3763–3768.

Reynolds, W.D., and D.E. Elrick. (2005): Measurement and

characterizati on of soil hydraulic properti es. p. 197–252

Reynolds, W.D., and G.C. Topp. (2008): Soil water analyses:

Principles and parameters. p. 913–939.

Shams Emamzadeh E.S., Soltani, J., Mashal, M., Kalanaki, M.,

and Asadolahzadeh, T., (2017): Performance Evaluation of

MLP and RBF Neural Networks to Estimate the Soil Saturated

Hydraulic Conductivity. Modern Applied Science; Vol. 11,

No. 3.

Simunek J., Sejna M., and Van Genuchten M.Th. (2006): The

HYDRUS software package for simulating two-and three-

dimensional movement of water, heat, and multiple solute in

variably-saturated media, Technical Manual, Version 1.11, PC

progress prague, Czech Republic.

Smola, A., Scholkopf, B. (1998): A tutorial on Support Vector

Regression. J. Statistics and Computing. 199 -222, 14 pages.

Vapnic, V. N., (1995): The Nature of Statistical Learning The-

ory. Springer Verlag, New York, USA.

Vapnic, V. N., (2010): The Nature of Statistical Learning Theory.

Springer Verlag, New York, USA.

Yang, S. and Y. Huang, (2007): Prediction of soil hydraulic

characteristic parameters based on support vector machine,

Chinese Society of Agricultural Engineering.

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS COMPARISON OF ACCURACY OF EPSILON AND QUADRATIC LOSS FUNCTION 101