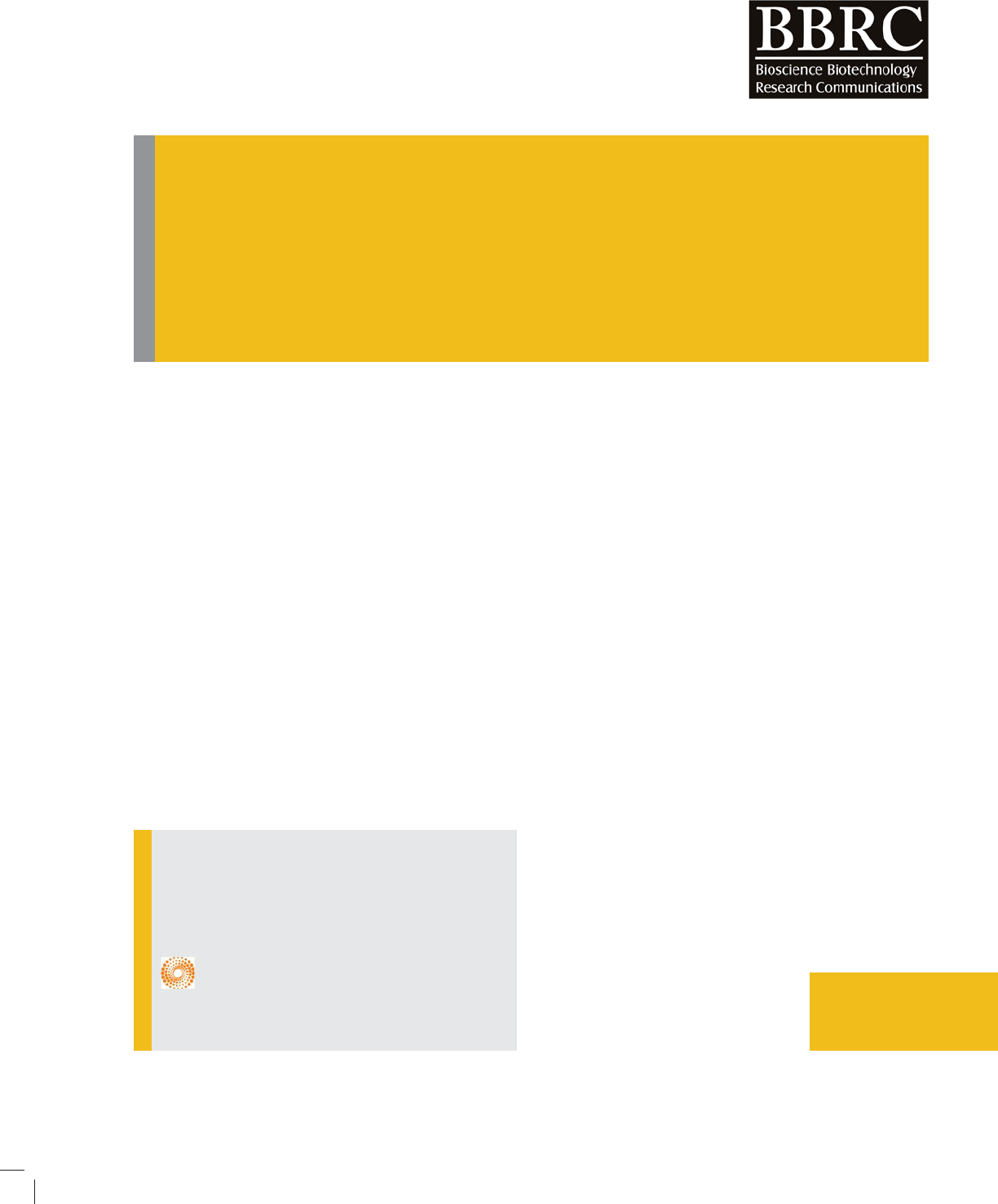
Forging pre-form dies optimization using arti cial

neural networks and continuous genetic algorithm

H. Hashemzadeh

, S.A. Eftekhari

and M. Loh-Mousavi

Msc student, Department of Mechanical Engineering, Khomeinishahr branch, Islamic Azad University,

Khomeinishahr, Iran

2,3

Assistant Professor, Department of Mechanical Engineering, Khomeinishahr branch, Islamic Azad

University, Khomeinishahr, Iran

ABSTRACT

In forging process of complex parts, the raw material cannot be transformed in one forging stage to the  nal shape;

therefore, using one or several pre-form dies would be necessary. An optimal pre-form die should be capable of

meeting several design criteria’s. Among such design criteria’s one can mention the defect-free parts manufacturing

with minimum raw materials, minimum plastic strain, minimum force requirement for ful lling the process as well

as  lling completely the  nal die. In this research, the Genetic Algorithm (GA) is used as a tool for Cartesian path

generation. For this reason, at  rst, several different pre-form dies are produced using random mathematical func-

tions. Then, using  nite elements simulation, the optimal die selection criteria’s are calculated. An arti cial neural

network (ANN) is learned by the data obtained from simulation so that it can predict the results of the simulation.

The ANN and design criteria’s are used as a target function for optimization using continuous GA. Finally, the best

pre-form die geometry is calculated using the continuous GA. Also this method is used for H-shape parts to evalu-

ate the method performance. The optimal pre-form die is recommended for the H-shape part and its forging results

extracted by the continuous GA. Also, the  nite element simulation performed for the optimal die and the obtained

results compared to the predicted results of the ANN. The results showed that the obtained optimal model meets the

prede ned criteria’s and this method can be used for optimization of pre-form dies successfully.

KEY WORDS: OPTIMAL PRE-FORM DIE, FINITE ELEMENT SIMULATION, ARTIFICIAL NEURAL NETWORKS, CONTINUOUS GENETIC ALGORITHM,

FORGING PROCESS.

ARTICLE INFORMATION:

*Corresponding Author: Hamidreza.hashemzadeh@iaukhsh.ac.ir

Received 1

Jan, 2017

Accepted after revision 2

April, 2017

BBRC Print ISSN: 0974-6455

Online ISSN: 2321-4007

Thomson Reuters ISI ESC and Crossref Indexed Journal

NAAS Journal Score 2017: 4.31 Cosmos IF : 4.006

reserved.

Online Contents Available at: http//www.bbrc.in/

Biosci. Biotech. Res. Comm. Special Issue No 1:74-86 (2017)

Hashemzadeh, Eftekhari and Loh-Mousavi

INTRODUCTION

Among manufacturing processes, forging process has a

particular importance, since it helps to produce parts with

excellent mechanical properties and minimum material

wastes. In forging, the raw material has a relatively sim-

ple shape. This material is transformed like wax during

one or more operations to a product with relatively com-

plex composition. Forging usually needs the relatively

expensive instruments. As a result, this process is attrac-

tive economically when the manufactured parts are in

mass volume or when special mechanical properties are

required for the  nal product. The material’s increasing

costs, energy and particularly the human force requires

that the forging processes and instruments are designed

with minimum trial and error and minimum possible

time. Therefore, making use of computerized methods,

i.e. CAE, CAM, CAD and particularly  nite elements

analysis-based computerized simulation is an absolute

requirement (Altan et al. 2006).

For H-shaped parts, considering complexity param-

eter, if the section height-to-width ratio be high, the part

shape would be complex and in order to produce it, the

pre-form die is needed. So far, there have been used dif-

ferent methods for pre-form die designing but none of

them is suitable for die optimal design.

Lanka et al. (1991) proposed a new method for

designing the pre-form dies in plane strain forgings.

In this method, the number of pre-form stages required

for the forging is investigated. The design criteria’s also

were stress rate and strain rate. Grandhi et al. (1993)

used design parameters control algorithm in forging

process. The mentioned parameters include dies velocity

for in-built strain rate control. They performed the anal-

ysis on solid and visco-plastic materials in  nite ele-

ments model. Zhao et al. (1995) provided the pre-form

die design using a node separation criterion in forging

reverse simulation with  nite elements model. In this

method, the complexity factor which shows the process

dif culty is used. Zhao et al. (1997) applied sensitivity

analysis model with  nite elements model for designing

pre-form dies in accurate forging. Also, the applicability

of this method in plane strain and axisymmetric forg-

ing was investigated. Using electrical  eld theory, Lee

et al. (2002) proposed a method for manufacturing the

axisymmetric parts’ pre-form in which the shape com-

plexity parameter is investigated. Then, using neural

networks the optimal die was obtained.

Abri Nia et al. (2006) obtained the dimensions and

coordinate of the part considering the contact time

parameters for middle dies of the H-shaped parts using

reverse transformation method-based algorithm as well

as nonlinear  nite elements model. Li et al. (2007) pre-

sented a novel intelligent optimization approach that

integrates machine learning and optimization tech-

niques. An intelligent gradient-based optimization

scheme and an intelligent response surface methodol-

ogy were proposed, respectively. Then optimization

algorithms implemented more effectively to  nd opti-

mal design results. An extrusion forging process and a U

channel roll forming process are studied as application

samples and the effectiveness of the proposed approach

is veri ed.

Bonte et al. (2010) used Sequential Approximate Opti-

mization (SAO) for optimizing forging processes. Three

variants of the SAO algorithm which differ by their

sequential improvement strategies have been investi-

gated and compared to other optimization algorithms by

application to two forging processes. The results showed

that SAO provides a very ef cient algorithm to optimize

forging processes using time-consuming FEM simula-

tions.

Khalili and Fonoudi (2010) investigated hot forging

process of AISI-1025 using Deform3D software. They

used an arti cial neural network to predict forging force

and strain based on the initial billet temperature, die

velocity, die displacement and friction between billet

and dies. The input data gathered using FEM simula-

tions. The obtained results showed that friction and die

displacement are the most effective parameters on the

forging force respectively.

Hosseinzadeh et al. (2010) outlined the Taguchi opti-

mization methodology, to optimize the effective param-

eters in forming cylindrical cups by the new die set

of sheet hydroforming process. It was shown that the

Taguchi method is suitable to examine the optimization

process. Khalili et al. (2011) studied the optimum blank

shape design for the deep drawing of Elliptical-shape

cups with a uniform trimming allowance at the  ange.

In this research, a new method for optimum blank shape

design using  nite element analysis has been proposed.

For this reason they applied Response Surface Meth-

odology (RSM) with Reduced Basis Technique (RBT)

to assist engineers in the blank optimization in sheet

metal forming. The proposed method is found to be very

effective in the deep drawing process and can be further

applied to other stamping applications. Lu et al. (2011a)

investigated three direct search algorithms, i.e. a modi-

 ed simplex, random direction search and enhanced

Powell’s methods together with a new localized response

surface method and applied to solve die shape optimiza-

tion problems in metal forming processes. Their main

motivation is to develop ef cient and easy to implement

optimization algorithms in metal forming simulations.

The optimization results from the three case prob-

lems show that direct search based methods especially

the modi ed simplex and the localized response surface

methods are computationally ef cient and robust for

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS 75

Hashemzadeh, Eftekhari and Loh-Mousavi

net-shape forging and extrusion optimization problems.

It is also suggested that these methods can be used in

more complex forging problems where die shape design

and optimization are essential for achieving net-shape

accuracy.

Lu et al. (2011b) based on the evolutionary structural

optimization (ESO) concept, developed a topological

optimization method for preform design. In this method,

a new criterion for element elimination and addition on

the work piece boundary surfaces is proposed to optimize

material distribution. Two 2D case problems including

forging of an airfoil shape and forging of rail wheel are

evaluated using the developed method. The results sug-

gest that the developed topology optimization method is

an ef cient approach for preform design optimization.

Shamsi-Sarband et al. (2012) utilized  nite element

method and sensitivity analysis for optimizing a preform

die shape in the superplastic forming (SPF) process. In

their study, the effect of friction coef cient on the opti-

mized preform die shape is investigated. They showed

that friction coef cient has an important effect on the

optimized preform die shape and thickness distribution.

Naeemi (2013) used the reverse transformation

method for designing the pre-form die and ANN for pre-

dicting the forging process and  nally, among 500 pre-

form dies designed, the optimal die meeting the design

criteria’s is selected. Shamsi-Sarband et al. (2013) used

a combination of sensitivity analysis and FEM to design

a preform for a two-stage superplastic forming process.

The results showed that the geometric parameters have

a signi cant effect on the preform shape. By increas-

ing the height and the cone angle of the  nal cup, the

depth of the preform in the inner cavity decreases and

the dome region is approached to the center of the pre-

form cup. By increasing the corner radius of the  nal-

die, only the height of the dome region decreases. Shao

et al. (2015) presented a recent work on preform design

optimization in bulk metal forming process based on a

topological approach. In the paper, to obtain a forging

preform shape with reduced material consumption but

enhanced uniform material deformation, a new element

removal and addition criterion has been established

with consideration of hydrostatic stress and strain com-

ponents. They implemented their method to forging of

a 3D aero engine blade. Considering the feasibility of

producing a preform, different constraints are applied in

the optimization process to affect the preform shape. The

optimization results suggest that the developed topol-

ogy optimization method is an ef cient approach for 3D

preform design and optimization.

In this research, the capability of continuous GA for

Cartesian path generation is used as a tool for die shape

optimization. At  rst, several different pre-form dies are

produced by random mathematical functions. Assuming

that the selected part is axisymmetric, one can simulate

it as a 2D die; therefore, a univariate function is used

for producing the parts die shape. Then, the optimal die

selection criteria are calculated using process simulation

in ABAQUS software. The design criteria’s considered

include  nal die’s  lling percentage, maximum force

exerted on the  nal die and the part’s maximum plas-

tic strain. The ANN has been taught using the infor-

mation obtained from simulation so that the relation-

ship between die shape and optimal design criteria’s are

simulated. These networks can be used as target func-

tion in the continuous GA. Finally, the best pre-form

die shape is recommended using continuous GA which

is a mathematical function and by plotting this function

in Cartesian coordination system, the die shape would

be obtained. This model is used for H-shaped parts to

evaluate the method performance.

MATERIAL AND METHODS

FORGING PROCESS

In forging, a part with primary shape is transformed

between 2 instruments (dies) like a wax until it reaches

the  nal desirable shape. Therefore, a simple part geom-

etry becomes complex in this way that the instrument

forms the desirable geometry on the part and the pres-

sure is exerted via the contacting surfaces between die

and material on the transforming material. Today, the

forging process is of signi cant importance in industry

and this is due to its advantages. In the following some

of them are mentioned:

- The forging parts are designed in such a form they have

the  nal product’s geometry as much as possible. Hence,

in this process the material wastes would be minimum

relative to the machining one.

- Due to lack of gas bubbles or suck which is observed in

other processes such as welding and casting, the parts’

mechanical and physical properties would be better in

forging.

- Due to the fact that in forging the die walls control the

material  ow, the part’s mechanical properties would

improve signi cantly.

As a consequence, potential economical energy and

material use would be resulted from forging; particu-

larly in average-high production quantities in which

the instrument cost can be easily depreciated. Forging

is a process based on experience. For years, the techni-

cal knowledge and experience in this  eld have been

obtained using trial and error methods. However, the

forging industry was capable to supply complex prod-

ucts from new alloys with minimum plasticity (Altan et

al. 2006). Physical phenomena which de nes a forging

76 FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Hashemzadeh, Eftekhari and Loh-Mousavi

process is hardly explainable using quantitative rela-

tions. Metal  ow, friction in material and die contact-

ing surface, heat production and transfer during waxy

 ow as well as process conditions and properties are

dif cult to predict and analyze. Often, in separate parts

manufacturing, several forging processes (pre-forming)

are required to transform the simple primary geometry

to a complex one without material defect or degradation

of properties (Altan et al. 2006).

2.2 Optimal pre-form die design using continuous GA

and ANN

2.2.1 H-shaped part’s properties and geometry

In  gure 1 the assumed part is indicated with its dimen-

sions in mm. For modeling this part in ABAQUS, ¼ of

the part is considered as indicated in  gure 2.

Final die shape and raw material for H-shaped part

forging

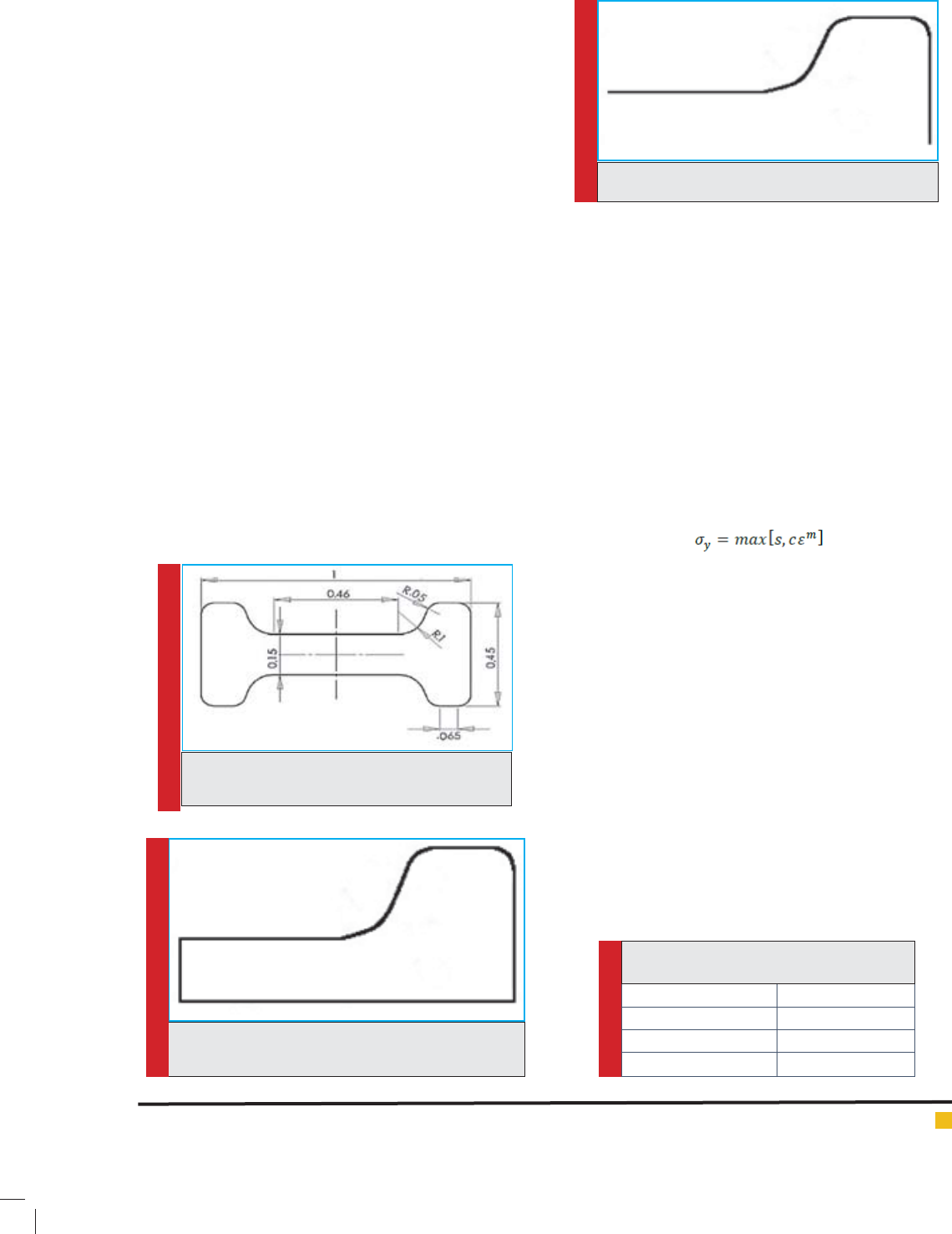
Considering the part shape, its  nal die is modeled as

curve-shaped as showed in  gure 3. The pre-form die for

this part is also similar to the curve-shaped  nal die. Of

course, there would be a narrow path in  nal die for bet-

ter material  ux and the extra materials are extracted as

pleated one. The raw part is considered for a cylindrical

die with height of 0.9 m and radius of 0.3 m. since the

raw part is axisymmetric, for its modeling ¼ of the part

is used which is rectangular with height of 450 mm and

width of 300 mm.

Raw material physical properties

AL2014 is selected as raw material. Since, forging

processes are performed in high temperature (400° C),

the elastic and plastic properties of this aluminum are

required in high temperature. These properties are (Altan

et al. 1983):

- Primary yield stress=23.7 MPa

- Poisson’s coef cient= 0.33

- Elasticity module=27.8 GPa

- Stress-strain relationship in plastic state

(1)

In this equation, s is the primary yield stress, c is the

 ow constant and m is the strain-rate hardening which

are c=1.02e8 MPa and m=0.11 for aluminum at 400° C.

2.2.4 The required pre-form phases’ number

In forging, at  rst the required number of pre-form

phases’ has to be determined. For this purpose, one can

make use of trial and error method or proposed meth-

ods in the previous articles. In this research, considering

the H-shaped part for forging, in order to determine the

pre-form phases’ number, the Thomas’ method is used.

Considering the part’s height-width ratio, the number of

phases required is listed in Table 1.

Considering the part’s dimensions used in this

research, only one pre-form phase is needed. For this

reason, the part forging includes 2 stages. At the  rst

phase, pre-form and in the second stage the  nal die

would be applied.

FIGURE 1. H-Shaped part geometry (Abri Nia

et al. 2006)

FIGURE 2. Part required geometry for modeling in

ABAQUS

FIGURE 3. Die’s  nal shape

Table 1. Number of required pre-forms

based on height-width ratio

height-width ratiorequired pre-forms

0-2No need to pre-form

2-31 pre-form phase

3 and more2 pre-form phases

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS 77

Hashemzadeh, Eftekhari and Loh-Mousavi

2.2.5 Mathematical function used for the H-shaped

part’s pre-form

The pre-form’s geometry is estimated from mathematical

functions and the  nal die shape. Figure 4 demonstrates

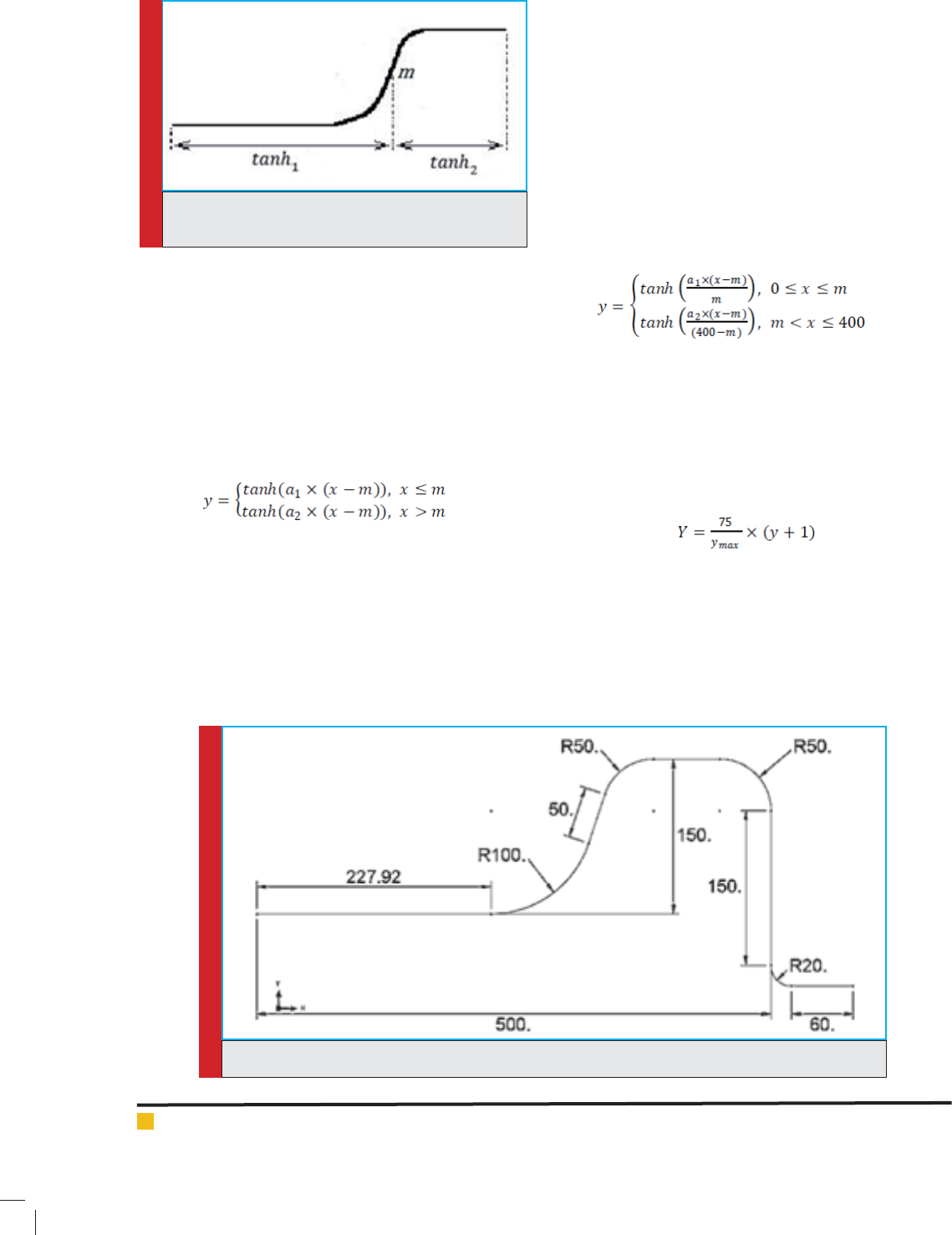
the mathematical functions used for pre-form die shape

estimation. This curved-shape consists of 2 tangent

hyperbolic functions interconnected in point m.

Equation 2 expresses the combination of these 2

functions as a new function.

(2)

In this relation, x is the pre-form die’s width coordinate,

y is the pre-form die’s height coordinate before mapping,

and a

are hyperbolic tangent functions’ coef cients

and m is the interconnection point of both functions.

The pre-form die’s dimensions are selected accord-

ing with the  nal part shape and primary part shape.

Considering that the part forging process has one

pre-form phase, the pre-form die shape is consid-

ered a middle shape between  nal part and primary

part’s shapes. The curve width formed by equation 2

is selected between the primary part’s width (300 mm)

and the  nal part’s width (500 mm) which would be

400 mm. also, change of its height equals half of the

 nal part’s height change (150 mm). As a result, the

pre-form die height would be 75 mm. therefore, the die

width and height intervals would be [0, 400] and [0, 75]

respectively. Relations 3 indicates the function used in

equation 2 which is mapped in to the required width

interval.

(3)

In equation 3, x is the pre-form die width coordinate; y

is the pre-form die height coordinate before mapping,

and a

are hyperbolic tangent functions coef cients

and m is interconnection point of both functions. Rela-

tions 4 indicates the function used in equation 3 which

is mapped to the required width interval. This equation

is the  nal problem relation.

(4)

In this equation, y is the pre-form die height coordinates

before mapping, Y is the pre-form die height coordinate

after mapping and y

max

is a point of pre-form die with

highest height.

FIGURE 4. Die’s shape estimation by mathematical

functions

FIGURE 5. Finaldiegeometry

78 FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Hashemzadeh, Eftekhari and Loh-Mousavi

RESULTS AND DISCUSSION

FINITE ELEMENTS SIMULATION AND RESULTS

OF FORGING

Required parts formation

The parts required for forging process simulation are raw

part, pre-form die and the  nal die which are modeled in

part setting of ABAQUS. All three parts are modeled in

axisymmetric form.

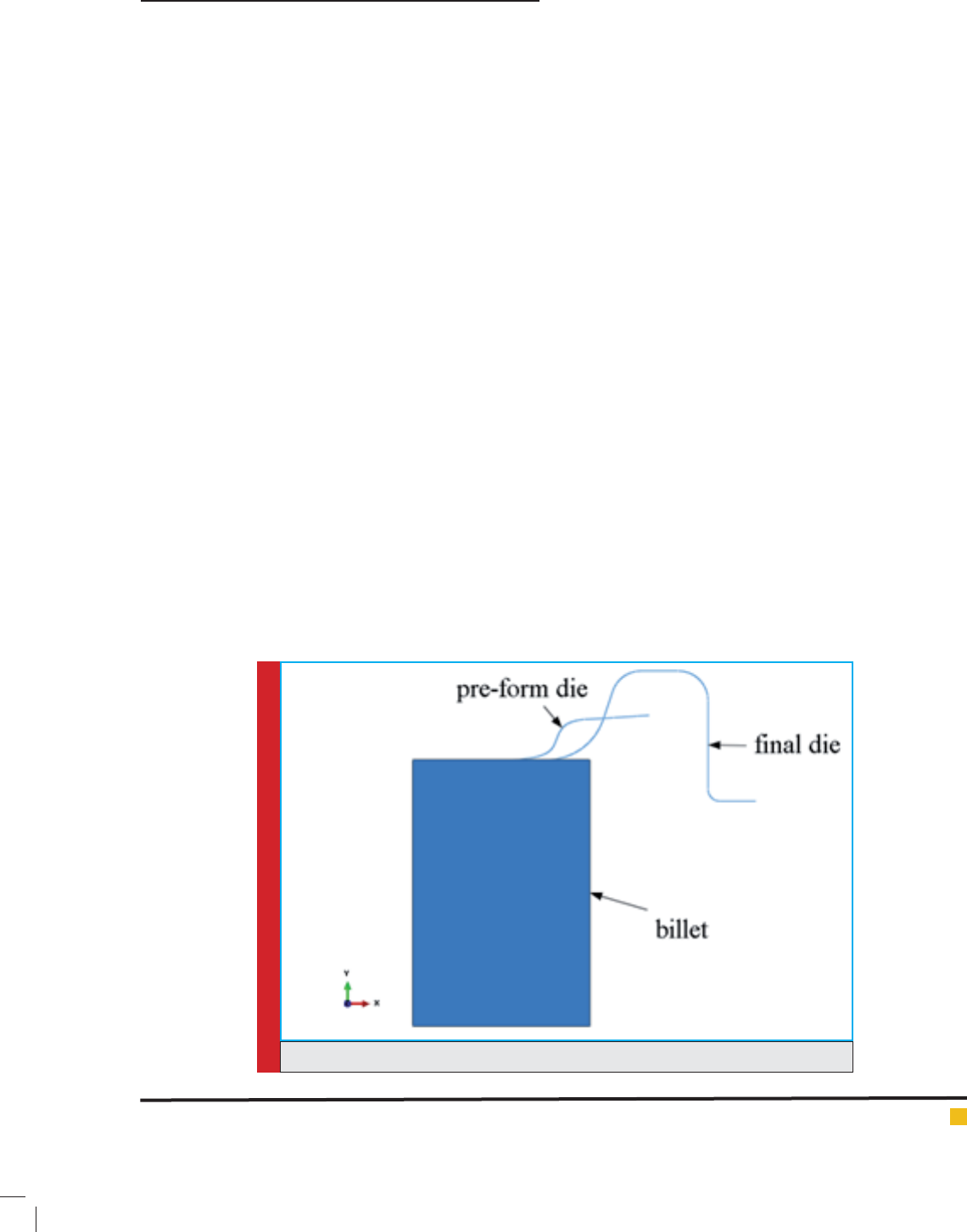
In case of pre-form die, the part is modeled in ana-

lytic rigid type and wire-shaped. The raw part which is

modeled from deformable type and shell-shaped one. In

case of  nal die, similar to pre-form die, the modeling

was analytic rigid type and wire-shaped. The  nal die

geometry is indicated in  gure 5.

Parts assembly

For parts assembling, the left end of pre-form and  nal

die is places on the top surface of the raw part. Figure 6

indicates the parts assemble.

Loading and boundary conditions de nition

In this subsection, motion and the loading as well as

parts boundary conditions are determined. In this pro-

cess, loading condition is applied in the form of die dis-

placement. In the  rst phase, the pre-form die moves

down 187.5 mm and in the second phase the  nal die

moves down 375 mm. The die’s motion type is also

selected as smooth step.

In case of boundary conditions, for all motion steps,

the axis line of the raw part is in horizontal direction

and its rotation is about the vertical axis on the surface.

The down surface of the raw part is also  xed in the

vertical direction.

Part meshing

This section deals with the suitable meshing in order

to solve the problem. The pre-form and  nal dies need

no elements due to their  nal selection as rigid body

and the only raw material needs meshing. Element type

for raw part is CAX4R. This element is of quadrilateral

axisymmetric and 4-node type reduced by integration.

The suf cient elements number for part meshing is

selected as 2128 to reach convergence.

Problem solving results demonstration

In this research, in order to  nd  lling percentage, the

Photoshop software is used. For this reason, at  rst the

simulation result obtained from the ABAQUS with format

of PNG is stored with the resolution of 1056×453 pixels.

Then, the PNG  le is loaded in Photoshop and the pleated

zone is removed and using its analysis tool, the num-

ber of pixels for the  nal part is calculated. Comparing

this number of pixels with the  nal die pixels number in

completely  lled state, the  lling percentage of the die

is obtained. The next parameter obtained from simula-

tion is the maximum force required for forging. As it is

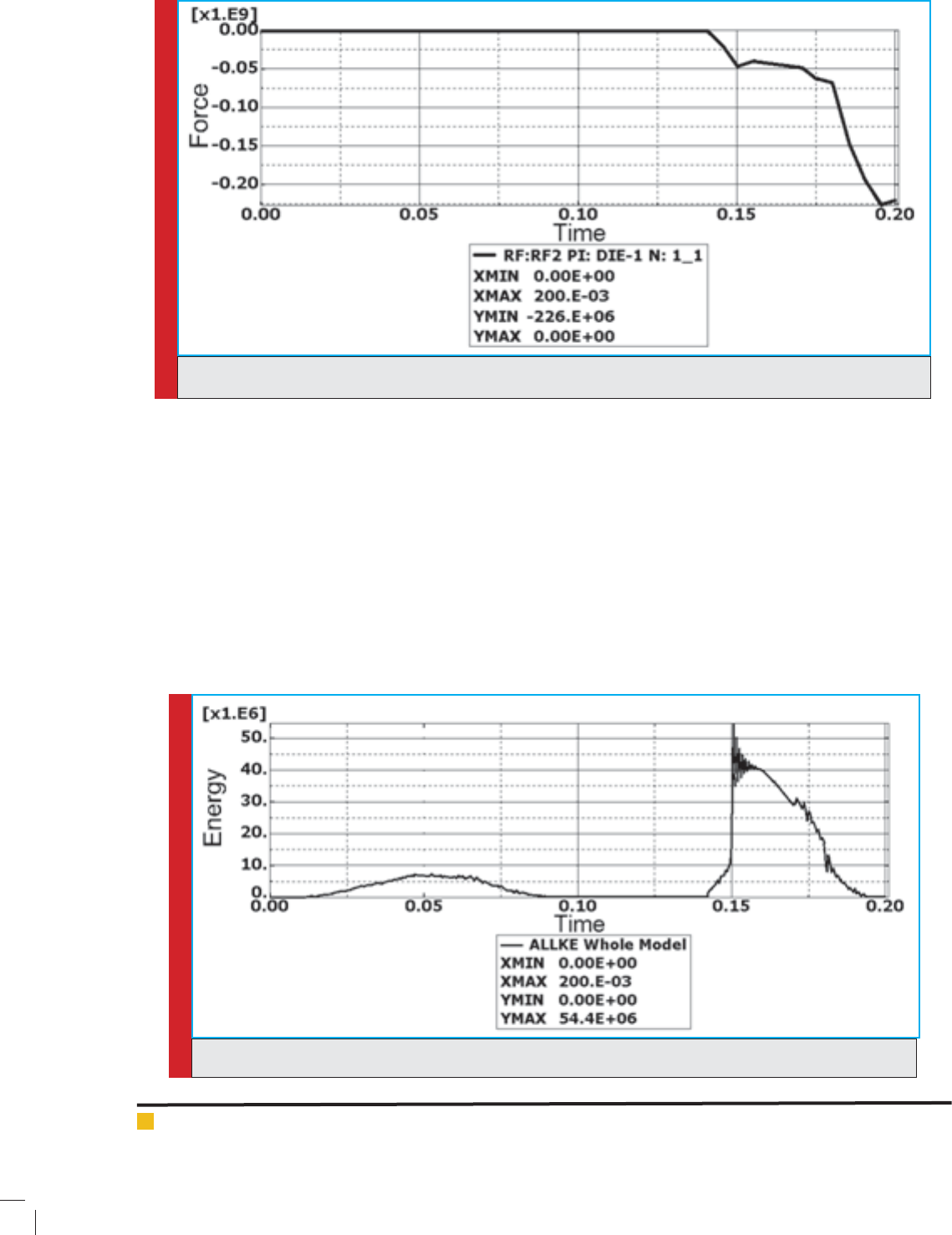
seen in  gure 7, plotting the diagram of exerted force on

the  nal die against time, one can obtain this maximum

force. Maximum force required for this model is 226 MN.

Simulation validating

In order to validate simulation and results, several check

points are implied as follows.

FIGURE 6. Parts assemble

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS 79

Hashemzadeh, Eftekhari and Loh-Mousavi

FIGURE 7. Force diagram against time for  nal die

FIGURE 8. Kinetic energy diagram during process

Kinetic energy-internal energy ratio

In cases the mass scale method is used for problem solv-

ing, the energy ratio should be validated. For validating,

the maximum kinetic energy-maximum internal energy

ratio is used. The value of this proportion should not be

more than 0.1. This means that the maximum kinetic

energy is 10% of the maximum internal energy. Figure

8 represents the kinetic energy and  gure 9 shows inter-

nal energy diagram against time. These diagrams can be

helpful in calculating the maximum kinetic and internal

energy.

As it is observed from  gures 8 and 9, the maximum

kinetic energy value is 54.4 MN/m and maximum inter-

nal energy value is 16.2 GN/m. the ratio of these ener-

gies is about 0.34% which is acceptable.

Evaluation of elements’ number and results convergence

Making use of suf cient elements in order to make sure

the solutions’ validity is of signi cant importance. Lower

elements than the necessary level causes wrong solu-

tions. Following, if the elements’ number be more than

the necessary level, this would not cause large changes

80 FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Hashemzadeh, Eftekhari and Loh-Mousavi

in the solution and only takes more time to solve the

problem which is costly. Here, for validating the simula-

tion, the necessary results of the problem for 8 different

number of elements are calculated and the results are

listed in table 2.

As it is seen from the above table, the output param-

eters change signi cantly up to 2128 elements and after

that the changes are negligible.

3.1.6.3 Step time

The considered time for solving the problem in step

module is effective on the problem results. If the time

considered be very low, then the results would be wrong

and if the time was very high, then the software would

require more time for problem solving which leads an

increase in problem processing time.

Table 3 lists the results obtained from applying differ-

ent times in step module. As it is seen from results, 0.1

s seems suf cient.

It is important to note that due to the fact that the

process is isothermal and material properties are consid-

ered independent of temperature and strain rate, the step

FIGURE 9. Internal energy diagram during process

Table 2. Simulation results for different number of elements

Processing

time (s)

Maximum

force (MN)

Maximum

plastic strain

Die  lling

percentage

Elements

number

11.41343.13097.75150

60.501795.14598.61600

114.71905.48498.94950

166.42087.52598.881350

139.72177.33699.101734

306.622610.31699.362128

358.02249.25399.082301

385.322311.48999.142400

Table 3. Simulation results by applying different

step times

Maximum

force (MN)

Maximum

plastic strain

Die  lling

percentage

Step

time (s)

22210.56699.310.05

22111.25799.130.07

22610.31699.360.10

22010.83799.970.12

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS 81

Hashemzadeh, Eftekhari and Loh-Mousavi

time doesn’t signi cantly affect the output parameters

dramatically.

Finding an optimal pre-form die using ANN and

continuous GA

Designing an Arti cial Neural Network

Since the FEM simulation is very time consuming, an

ANN is used to estimate the forging process results for

different settings. A multilayer feed forward Percep-

tron network is chosen for this reason and the forging

process input and output data are used for learning the

network parameters. The network parameters include

weights and biases which should be adjusted in such a

way to optimize the network performance. The network

performance is considered the minimum error between

network outputs and targets. In order to optimize, one

must de ne a performance index. In this research, mean

square error is used as a performance index. MSE is

the most common and desirable error function used for

multi-layer networks.

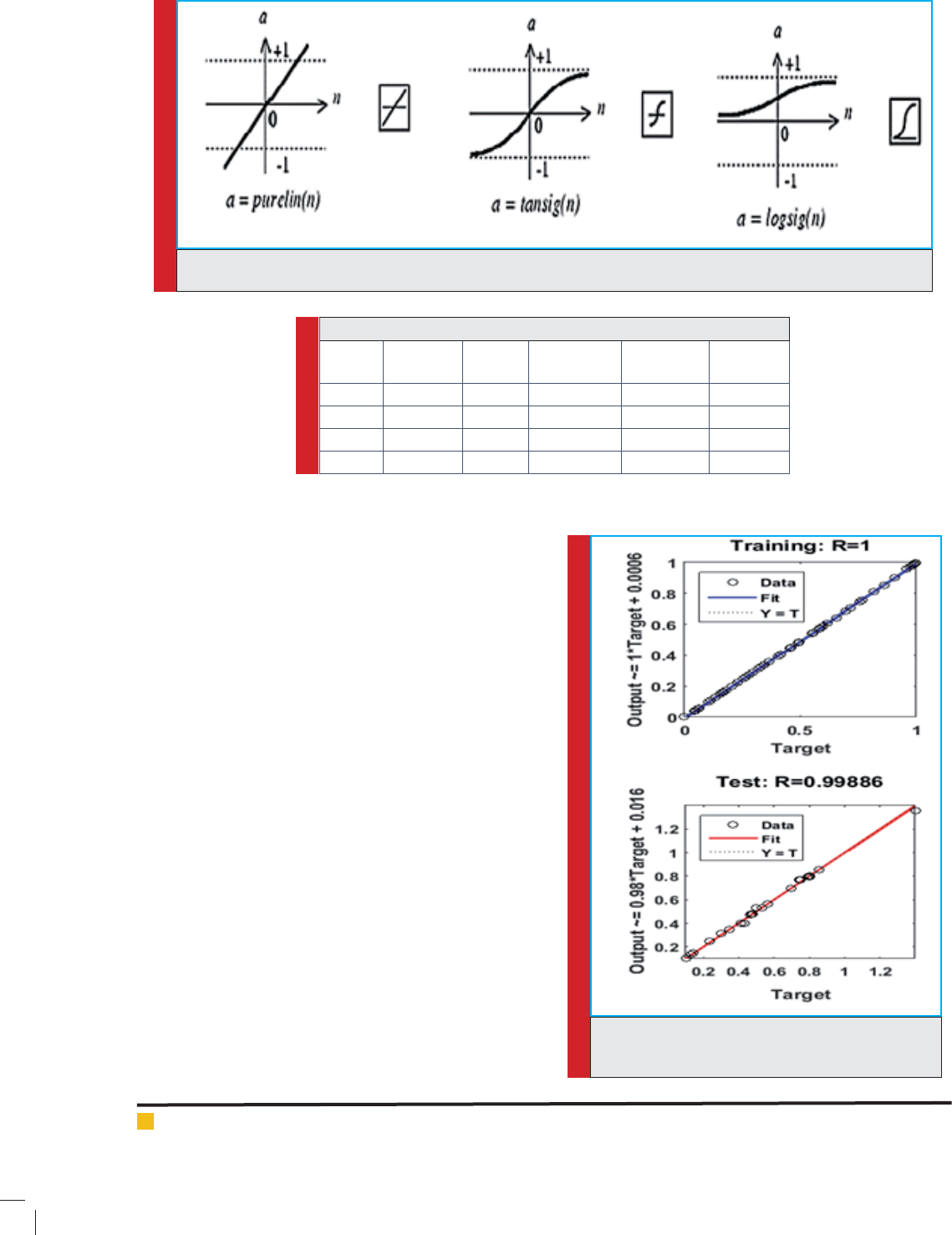
Transfer functions selection

Transfer functions are determined based on the require-

ments of a problem. Considering recent studies and

researches for correct results prediction from network as

well as making use of the back propagation method in

FIGURE 10. Widely used transfer functions in NN (Kia, 2010)

Table 4. Results obtained from networks run with different topologies

Maximum

error

Minimum

error

Correlation

coef cient

MSETopologySerial

0.47-0.330.870.00895,12,31

0.35-0.140.970.002312,15,32

0.10-0.210.940.0002118,12,33

0.05-0.030.990.0000520,40,34

FIGURE 11. Test and training correlation coef cient

diagram fortrained network

82 FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Hashemzadeh, Eftekhari and Loh-Mousavi

FIGURE 12. Network performance diagram

FIGURE 13. Fitness convergence and best generation in normal form

this research, the only requirement for these functions is

that they have to be differentiable in the whole domain,

since their differential is used in the learning process.

Among most applicable functions, the sigmoid and lin-

ear functions are used widely. Figure 10 indicates some

of these functions.

In this research, the sigmoid hyperbolic tangent func-

tions in network hidden layers and the linear transfer

function in last layer are used.

ANN Optimal topology

In this section, several neural networks are designed with

different topologies. Then, these networks are trained

and on the basis of performance index, the optimal net-

work is selected for this research. Of course, for training

the network, all data has to be normalized.

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS 83

Hashemzadeh, Eftekhari and Loh-Mousavi

Table 5. Results obtained from normal and real scale

Maximum

force (MN)

Maximum

plastic strain

Die  lling

percentage

a2a1m

Raw part’s

width

Scale

0.170770.30381.030.92140.42140.04810.5Normal

2718.887100.0613.99.6205.8302.5Real

FIGURE 15. Diagram of force exerted on the  nal die for optimal state

FIGURE 14. Plastic strain contour related to optimal state

Optimal network selection

Table 4 lists the results obtained from network run for

several different topologies. In this table, the numbers in

the topology column de nes the number of neurons in

different layers. As it is seen, the last network with three

layers containing 20 and 40 neurons in the hidden lay-

ers has the best MSE and correlation coef cient.

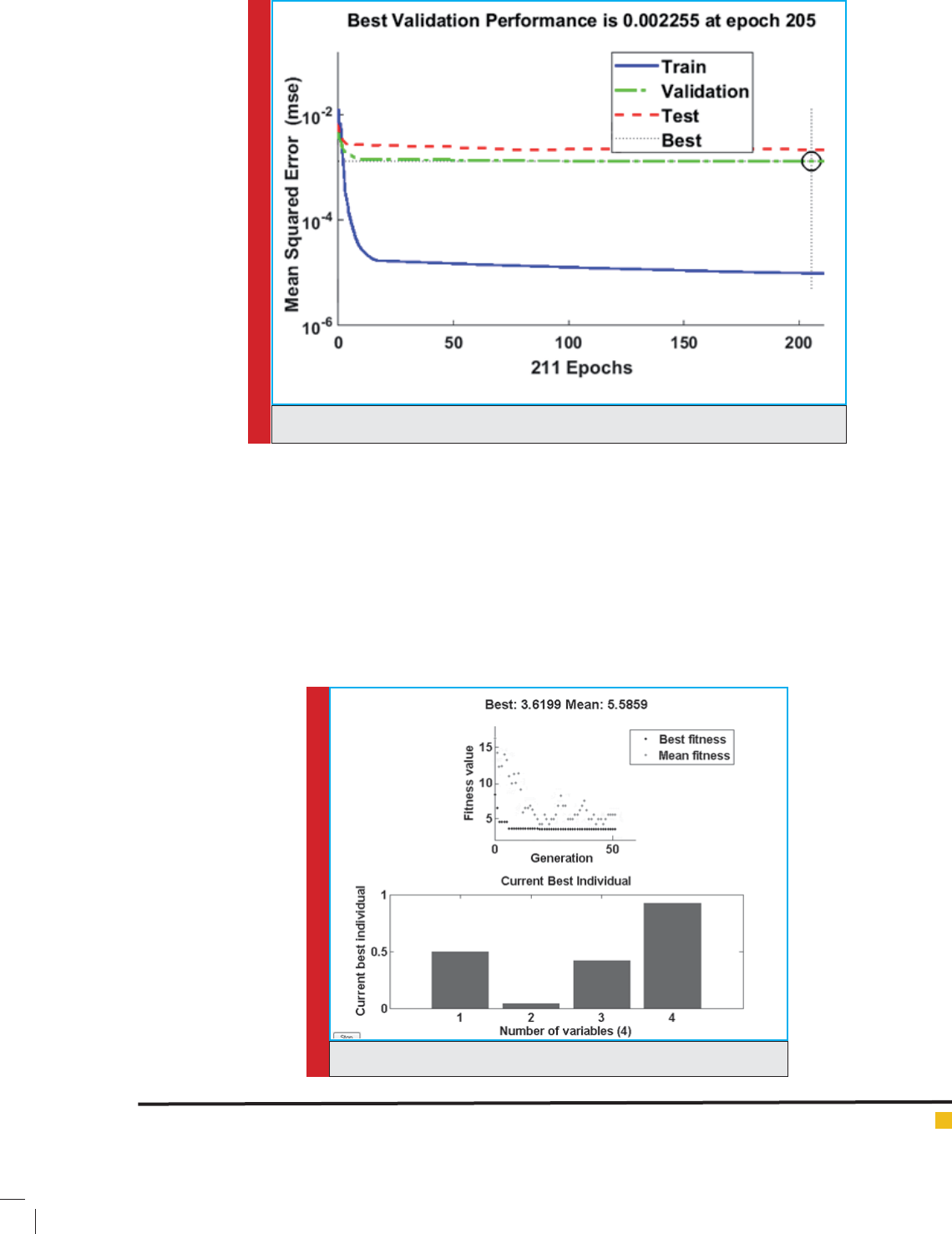
Figure 11 indicates the correlation coef cient for

training and test data and  gure 12 indicates the net-

work performance.

These  gures show the chosen network capabili-

ties, so this network would be used to simulate the

forging process as a  tness function in optimization

using GA.

3.2.5 The optimal pre-form die obtained by continuous

Figure 13 indicates the  tness convergence diagram and

the best generation diagram. It is notable that to make

sure the GA results are global minimum, the optimiza-

84 FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

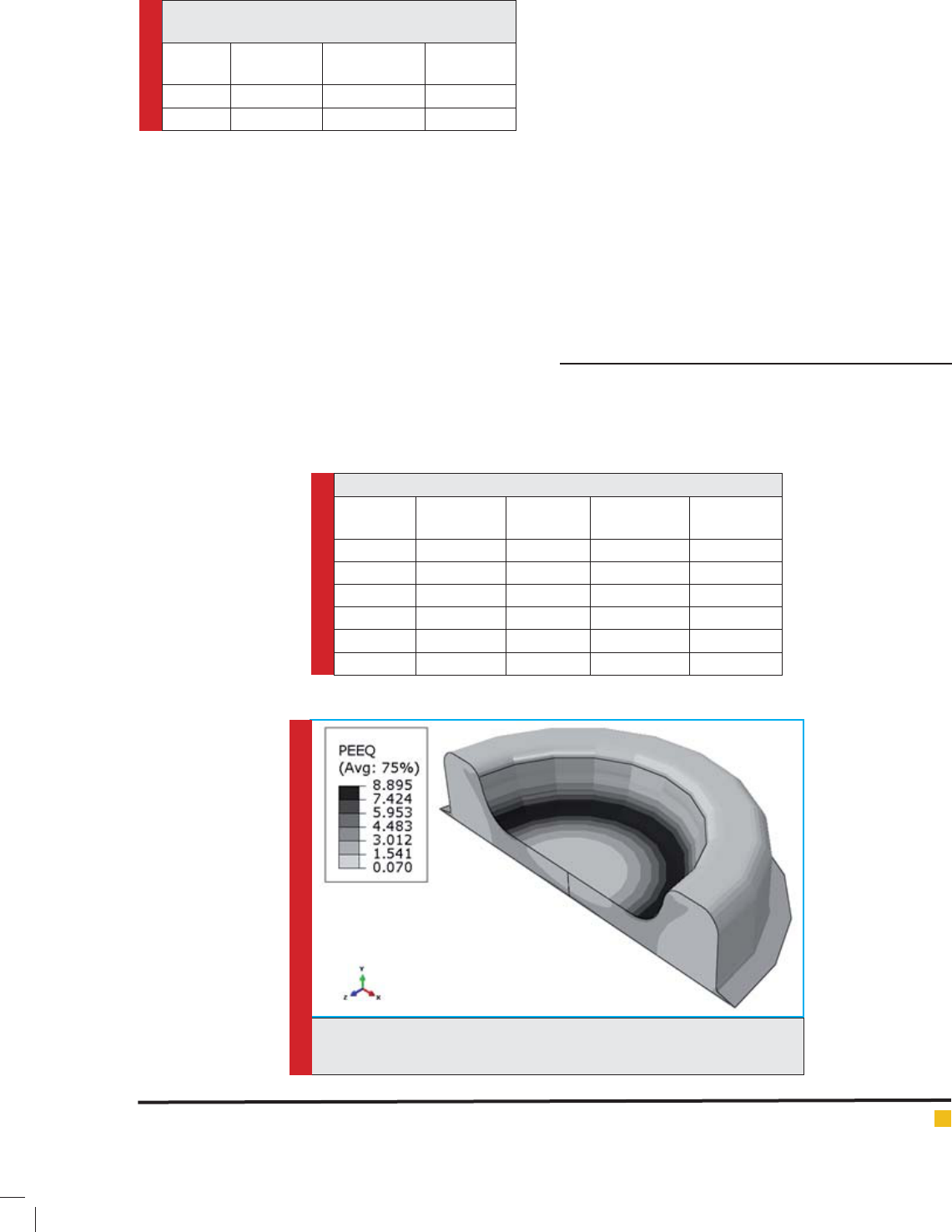
Hashemzadeh, Eftekhari and Loh-Mousavi

tic strain contour and  gure 15 indicates the exerted

force on the  nal die.

Table 6 lists the results of the optimal pre-form die

 nite element simulation in comparison with the results

obtained from the GA. As it is observable from the

results, there is very small difference between NN results

and ABAQUS results. This means that NN is designed

well and can predict the process as well.

To ensure the obtained result is the optimum state of

the pre-form die, several random states were simulated

and their FEM results are shown in the Table 7 in compar-

ison to best result obtained by the GA method. This table

proofs the optimality of GA results versus other states.

In  gure 16, the cut section of the optimal state of the

part is represented at the end of the  nal die application.

CONCLUSION

In this paper, necessity of using pre-form dies in forg-

ing process declared and pre-form die designing methods

were studied. Following, the GA capabilities were out-

Table 7. Comparison of GA result and  ve random states

Maximum

force (MN)

Maximum

plastic strain

Die  lling

percentage

Raw part’s

width

state

22310.25499.18300Random 1

2109.98598.91301Random 2

52413.83499.89302.5Random 3

53013.779100305Random 4

52813.51099.16304Random 5

2708.89599.96302.5best

Table 6. Comparison between  nite elements and GA

results

Maximum

force (MN)

Maximum

plastic strain

Die  lling

percentage

Results

2708.89599.96ABAQUS

2718.887100.06GA

FIGURE 16. Cut section of part for optimal state at the end of  nal die

application

tion process using GA is iterated 20 times and the best

result is considered so that its validity was assured.

Following, the best generation values are substituted

in neural network and its results were extracted. The

results obtained were in normal state; therefore, param-

eters values returned to their primary scale. Table 5 lists

the results obtained in normal and real scale.

3.2.6 Optimal pre-form die  nite element simulation

and results comparison

Using the optimized parameters obtained from the GA

method, the forging process is simulated in ABAQUS and

the results obtained would be compared to the results

obtained from the GA. Figure 14 demonstrates the plas-

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS 85

Hashemzadeh, Eftekhari and Loh-Mousavi

lined such as their application on continuous problems

optimization. It was indicated how to make use of math-

ematical functions in GA. Following, a new method for

designing the optimal pre-form dies was proposed. In this

method, without simplifying the pre-form die shape and

only using different mathematical functions combina-

tion, the optimal pre-form die shape was designed. To this

end, after selecting the suitable function for pre-form die

shape, several random pre-form die shapes were produced

and then using  nite elements model and ABAQUS soft-

ware, the pre-form die forging process was simulated and

results were extracted. These results were used for train-

ing the ANN, a network which can predict the forging

process performed in  nite elements model due to its time

consumption. Finally, using designed ANN and effective

parameters on forging, the target function required for

GA was formed and following the algorithm running, the

optimal pre-form die was obtained. This method was used

for an H-shaped part which was axisymmetric to evalu-

ate its performance. The results show that combination of

ANN and GA makes a powerful tool for designing com-

plex pre-form dies. Here, the method was used for a part

which needs only one step pre-form die, and may be used

for more complex parts with several pre-form dies to vali-

date its potential. Also the method can be extended using

more parameters including number of pre-form dies,  ux

stress, friction coef cient and so on. Finally comparison

of theoretical optimized results with experimental data is

suggested.

REFERENCES

Abri Nia K., M.H. Naie, Y. Taqi Put Lahijani, (2006): Pre-form

Forging Cast Design in Reverse Transformation and Finite Ele-

ments Method, Technical college magazine, Vol 40, pp 763-

769.

Altan T., G. Ngail, G. Shen, M.H. Hojati, (2006): fundamentals

of cold and hot forging, Mazandaran University Publication,

Babolsar.

Altan T., S. I. Oh, H. L. (1983): Gegel, Metal Forming: Funda-

mentals and Applications, American Society for Metal, Metals

Park.

Bonte M. H. A., L. Fourment, T. T. Do, A. H. Van Den Boogaard,

J. Huétink, (2010): Optimization of forging processes using

Finite Element simulations Structural and Multidisciplinary

Optimization, Structural and Multidisciplinary Optimization,

Vol 42, Issue 5, pp 797-810.

Grandhi R. V., H. Cheng, S. S. Kumar, (1993): Optimum Design

of Forging Process with Deformation and Temperature Con-

straints, ASME Advances in Design Automation, Vol 2, pp

583-593.

Hosseinzadeh M., M. Bakhshi-Jooybari, M. Shakeri, H. Mosta-

jeran, H. Gorji, (2010): Application of Taguchi Method in Opti-

mization of New Hydroforming Die Design, Steel Research

International, Vol 81, Issue 9, pp 647-650.

Khalili K., Fonoudi H., (2010): Simulation of Hot Forging Pro-

cess Using FEM and ANN Method to Predict Metal Forming

Parameters, the 12th Iranian Conference on Manufactoring

Engineering, SMEI University of Tehran, Iran.

Khalili K., P. Kahal, S. Eftekhari, M. S. Khalili, (2011): Blank

Optimization in Elliptical-shape Sheet Metal Forming Using

Response Surface Model Coupled with Reduced Basis and Finite

Element Analysis, Key Engineering Materials, Vol 473, pp 683.

Kia M., (2010): neural networks in MATLAB, Kian Rayaneh

Sabz publication.

Lanka S., R. Srinivasan, R. V. Grandhi, (1991): Design Approach

for Intermediate Die Shapes in Plane Strain Forgings, Journal

of Materials Technology, Vol 9, No 4, pp 193-206.

Lee S. R., Y. K. Lee, C. H. Park, (2002): A New Method of Preform

Design in Hot Forging by Using Electric Field Theory, Interna-

tional Journal of Mechanical Sciences, Vol 44, pp 773-792.

Li D.Y., Y.H. Peng, J.L. Yin, (2007): Optimization of metal-

forming process via a hybrid intelligent optimization tech-

nique, Structural and Multidisciplinary Optimization, Vol 34,

Issue 3, pp 229-241.

Lu B., H. Ou, H. Long, (2011a): Die shape optimisation for net-

shape accuracy in metal forming using direct search and local-

ised response surface methods, Structural and Multidiscipli-

nary Optimization, Vol 44, Issue 4, pp 529-545.

Lu B., H. Ou, Z.S. Cui, (2011b): Shape optimisation of preform

design for precision close-die forging, Structural and Multidis-

ciplinary Optimization, Vol 44, Issue 6, pp 785-796.

Naeemi A., (2013): Design and Optimization of Forging Pre-

form Casts in Reverse Transformation and ANN Methods, Msc.

Thesis, I.A.U, Khomeini Shahr University.

Shamsi-Sarband A., S. J. Hosseinipour, M. Bakhshi-Jooybari,

M. Shakeri, (2012): Study on the Effect of Friction Coef cient

on the Optimized Preform Die Shape in a Multistage Super-

plastic Forming.

Shamsi-Sarband A., S. J. Hosseinipour, M. Bakhshi-Jooybari,

M. Shakeri, (2013): The Effect of Geometric Parameters of

Conical Cups on the Preform Shape in Two-Stage Superplastic

Forming Process, Journal of Materials Engineering and Perfor-

mance, Vol 22, Issue 12, pp 3601-3611.

Shao Y., B. Lu, H. Ou, J. Chen, (2015): A new approach of

preform design for forging of 3D blade based on evolutionary

structural optimization, Structural and Multidisciplinary Opti-

mization, Vol 51, Issue 1, pp 199-211.

Zhao G., E.Wright, R. V. Grandhi, (1997): Sensitivity Analysis

Based Preform Die Shape Design for Net-Shape Forging, Inter-

national Journal of Machine Tools and Manufacture, Vol 37,

No 9, pp 1251-1271.

Zhao G., E.Wright, R.V. Grandhi, (1995): Forging Preform

Design with Shape Complexity Control in Simulating Back-

ward Deformation, International Journal of Machine Tools and

Manufacture, Vol 35, pp 1225-1239.

86 FORGING PRE-FORM DIES OPTIMIZATION USING ARTIFICIAL NEURAL NETWORKS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS