Deep learning techniques and their applications: A

short review

Vaibhav Kumar and M L Garg

Department of Computer Science & Engineering, DIT University, Dehradun, India

ABSTRACT

In recent years, there is a revolution in the applications of machine learning which is because of advancement and intro-

duction of deep learning. With the increased layers of learning and a higher level of abstraction, deep learning models

have an advantage over conventional machine learning models. There is one more reason for this advantage that there

is a direct learning from the data for all aspects of the model. With the increasing size of data and higher demand to

 nd adequate insights from the data, conventional machine learning models see limitations due to the algorithm they

work on. The growth in the size of data has triggered the growth of advance, faster and accurate learning algorithms.

To remain ahead in the competition, every organization will de nitely use such a model which makes the most accurate

prediction. In this paper, we will present a review of popularly used deep learning techniques.

KEY WORDS: DEEP LEARNING, MACHINE LEARNING, NEURAL NETWORKS

699

Biomedical

Communication

Biosci. Biotech. Res. Comm. 11(4): 699-709 (2018)

INTRODUCTION

Deep learning, a family of machine learning algorithms,

is inspired by the biological process of neural networks

is dominating in many applications and proving its

advantage over conventional machine learning algo-

rithms (Goodfellow et al, 2016). It is only because of

their capability in producing faster and more accurate

results. It attempts to model high-level abstraction in

data based on a set of algorithms (Deng et al, 2014). In

deep learning techniques, there is a direct learning from

the data for all aspects of the model. It starts with low-

est level features that present a suitable representation

of the data. It then provides higher-level abstractions

for each of the speci c problem in which it is applied.

Deep learning becomes more useful when the amount

of training data is increased. The development of deep

learning models has increased with the increase in the

software and hardware infrastructure (Aghdam et al.,

2017, Nisbet et al, 2018).

ARTICLE INFORMATION:

Corresponding Authors: vaibhav05cse@gmail.com

Received 19

Sep, 2018

Accepted after revision 23

Dec, 2018

BBRC Print ISSN: 0974-6455

Online ISSN: 2321-4007 CODEN: USA BBRCBA

Thomson Reuters ISI ESC / Clarivate Analytics USA

Mono of Clarivate Analytics and Crossref Indexed

Journal Mono of CR

NAAS Journal Score 2018: 4.31 SJIF 2017: 4.196

Online Contents Available at: http//www.bbrc.in/

DOI: 10.21786/bbrc/11.4/22

Nitesh Malhotra and Aksh Chahal

700 DEEP LEARNING TECHNIQUES AND THEIR APPLICATIONS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Deep learning models use multiple layers which are

the composition of multiple linear and non-linear trans-

formations. With the increase in the size of data, or with

the developments in the  eld of big data, conventional

machine learning techniques have shown their limita-

tion in analysis with the size of data (Chen, 2014). Deep

learning techniques have been giving better results in

this task of analysis. This technique has been introduced

worldwide as breakthrough technology because has dif-

ferentiated machine learning techniques working on old

and traditional algorithms by exploiting more human

brain capabilities.It is useful in modeling the complex

relationship among data. Instead of working on task-

speci c algorithms it is based on learning data represen-

tations. This learning can be supervised, unsupervised or

semi-supervised, (Hoff, 2018).

In deep learning models, multiple layers composed of

non-linear processing units perform the task of feature

extraction transformation. Every layer takes the input

as the output of its corresponding previous layer. It is

applied in classi cation problems in a supervised man-

ner and in pattern analysis problems in an unsupervised

manner. The multiple layers which provide the high-level

abstraction, form a hierarchy of concepts. There are deep

learning models which are mostly based on arti cial neu-

ral networks which are organized layer-wise in deep gen-

erative models. The concept behind this distributed repre-

sentation is the generation of observed data through the

interaction of layered factors. The high-level abstraction

is achieved by these layered factors. A different degree of

abstraction is achieved by varying the number of layers

and the size of layer (Najafabadi et al, 2015).

The abstraction is achieved through learning from the

lower level by exploiting the hierarchical exploratory

factors. By converting the data into compact immediate

representations of principal components and removing

redundancies in representation through derived layered

structures, the deep learning methods avoid feature engi-

neering in supervised learning applications. In unsuper-

vised learning where unlabeled data is more abundant

than labeled data, deep learning algorithms can be applied

to such kind of problems. The deep belief networks are

the example of deep learning model which are applied to

such unsupervised problems, (Auer et al., 2018).

Deep learning algorithms exploit the abstract repre-

sentation of data which is because of the fact that more

abstract repetitions are based on less abstraction. Due to

this fact, these models are invariant to the local changes in

the input data. This has the advantage in many pattern rec-

ognition problems. This invariance helps the deep learning

models feature extraction in the data. This abstraction in

representation provides these models the ability to separate

the different sources of variations in data. The deep learn-

ing models outperform old machine learning models by

manually de ning the learning features. This is because of

the fact that it relies on human domain knowledge rather

than relying on available data and the design of models

are independent of the system’s training.

There are many deep learning models developed by

the researchers which give a better learning from the

representation o arge-scaleunlabeled data. Some popu-

lar deep learning architectures like Convolutional Neu-

ral Networks (CNN), Deep Neural Networks (DNN), Deep

Belief Network (DBN) and Recurrent Neural Networks

(RNN) are applied as predictive models in the domains

of computer vision and predictive analytics in order to

 nd the insights from data. With an increase in the size

of data and necessity of producing a fast and accurate

result, deep learning models are proving their capabili-

ties in the task of predictive analytics to address the data

analysis and learning problems.

Since, there are various deep learning techniques are

in existence and each of these has a speci c application

due to their working model. So, it is necessary to review

these models based on their working and applications.

In this paper, we now present a review of popular deep

learning models focused on arti cial neural networks.

We will discuss ANNs, CNNs, DNNs, DBNs,and RNNs

with their working and application.

ARTIFICIAL NEURAL NETWORK

Arti cial Neural Network is a computational model

inspired by the biological neural networks. Billions of neu-

rons are connected together in the biological neural net-

work which receives electrochemical signals from it neigh-

boring neurons. They process these signals and either store

them or forward to the next neighboring neurons in the

network (Yegnarayana, 2018, Garven et al, 2018).

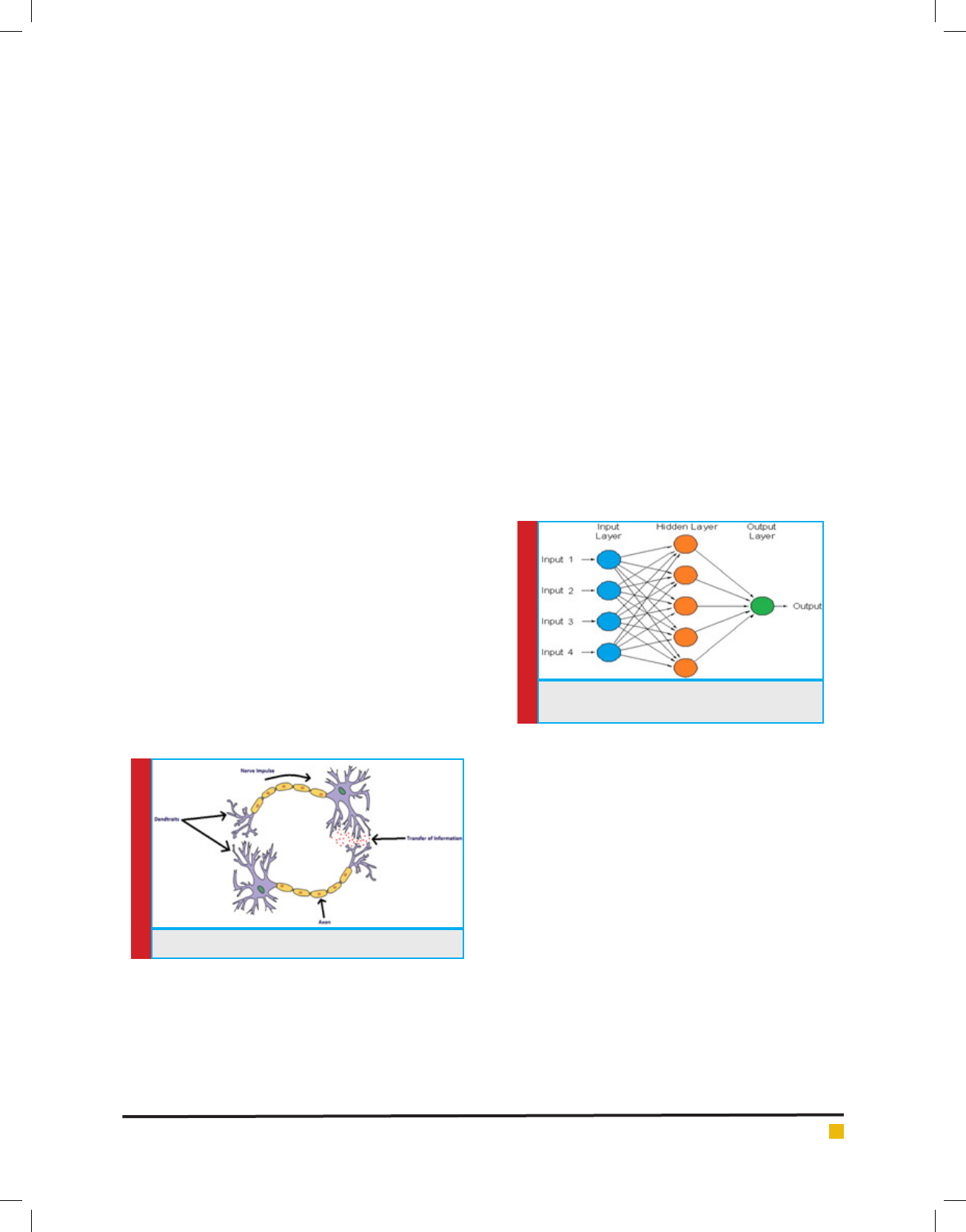
It is represented in  gure 1 given below.

Every biological neuron connected to the neighbor-

ing neurons and communicate to eachother. The axons

in the network carry the input-output signals. Theyre-

ceive the inputs from the environment which create the

impulse in form of electrochemical signals which travel

quickly in the network.A neuron may store the informa-

tion or it may forward it to the network. Theytransfer

the information to the neighbors through theirdendrites.

Arti cial neural networks work similarly to the work-

ing of biological neural networks. An ANN is an inter-

connection of arti cial neurons. Every neuron in the

layer is connected to all the neurons of previous and

next layers. There is a weight given as the labels at each

interconnection between neurons.Each neuron receives

input which is the output of neurons of the previous

layer. They process this input and generate an output

which is then forwarded to the neurons of next layer.

There is an activation function used by each neuron of

Nitesh Malhotra and Aksh Chahal

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS DEEP LEARNING TECHNIQUES AND THEIR APPLICATIONS 701

the network which collects the inputs, sums the inputs

and generate the output (Hop eld, 1988). There are vari-

ous types of activation functions which are chosen on

the basis of required output.

A simple arti cial neural network is composed of

three layers. The input layer, the hidden layer and the

output layer. The inputs in the form of input vector are

applied to the input layer. The number of neural nodes

in the input layer depends on the number of attributes

in the input. The output of each neuron at input layer is

forwarded to every neuron of hidden layer where they

are received as inputs. The hidden layer is also referred

as the processing layer. Because this is the main layer

where the processing is performed on inputs. The num-

ber of nodes at hidden layer are decided randomly  rst

and it may be adjusted during training. The outputs of

each neural node at hidden layer is then forwarded to

output layer where they are received as inputs. The out-

put layer then generates the output which is collected as

 nal output of the network. The number of nodes at out-

put layer depends on the type of output(Abraham, 2005).

In classi cation problems, the number of nodes are same

as the number of classes the inputs are to be assigned. In

regression problems, there may be only output node to

produce an output value.

On the basis of layers, there are two types of feed-

forward arti cial neural networks. The  rst type is the

single layer feed-forward ANN and the second type is

the multilayer feed forward neural network. In a single

layer, there is no any hidden layer in the network. It

is the simplest kind of neural network. The network is

composed of the input layer and the output layer only.

The inputs applied to the input layers are directly for-

warded to the output layer for generating the outputs.

applications. A feed-forward network is one where the

signals travel in one direction only that is the forward

direction, means from the input layer to the output layer

(Bebis et al, 1994). There are feed-backward or feedback

neural networks which we will discuss later in this chap-

ter. Every neural network works on some learning algo-

rithm.

There are various types of learning algorithms which

are selected depending on the problem to which the net-

work is being used. The training of the networks is done

by implementing the learning algorithm. Backpropaga-

tion learning algorithm is very popular and applied in

many applications to train the neural network. It adjusts

the weight of interconnections using error in output at

a layer. This error is propagated in the backward direc-

tion to the previous layers. That is why it is called back-

propagation algorithm (Buscema, 1998). There are many

other algorithms for each supervised and unsupervised

training of the network. The architecture of a feed-

forward neural network is represented in  gure 2 given

below.

FIGURE 1. Biological Neural Network

FEED-FORWARD ARTIFICIAL

NEURAL NETWORK

There are various types of arti cial neural networks each

has a speci c property and can be applied in a differ-

ent problem domain. Feed-forward structure of arti cial

neural networks have been used very popularly in many

FIGURE 2. Feed-Forward Arti cial Neural

Network

In above  gure, the architecture of a feed-forward

neural network is represented. This network is a compo-

sition of arti cial neurons where every neuron is con-

nected to the neurons of its previous and next layers.

During training of the network, the inputs in form of a

vector are applied to the vector of neural nodes at input

layer. In many learning algorithms, a bias input is also

applied to the main input. This bias value is  xed during

the training. The  rst input pattern is applied and it is

transferred to the hidden layer. The activation function

used at neurons generate the output which is collected

at the output layer. In classi cation problems, the step

functions are generally used and in regression problems,

the logistic problems are used. The training of the net-

work is performed on the dataset in many epochs. Some

algorithms use gradient descent to stop the training pro-

cess after reaching to certain error.

Let the inputs I

, I

… , I

are applied to the input layer

of the network, then the net input received at a single

neuron ofhidden layer is:

Nitesh Malhotra and Aksh Chahal

702 DEEP LEARNING TECHNIQUES AND THEIR APPLICATIONS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Where w is the weight on interconnection and b is the

bias value, and hence the net input received at the hid-

den layer, if there are m neurons, is represented in the

form of a vector as:

values reach toa certain threshold, the neurons start  r-

ing the output which is called that the neuron is acti-

vated. For this activation, a function is used which maps

the net input received to the neuron with the output.

This function is called the activation function. There are

various types of activation functions used at neurons

depending on the problem to which the neural network

is being applied (Roy, Chakraborty, 2013). The popularly

used activation functions are the step function and the

sigmoid function. Here we will present a brief descrip-

tion of these functions.

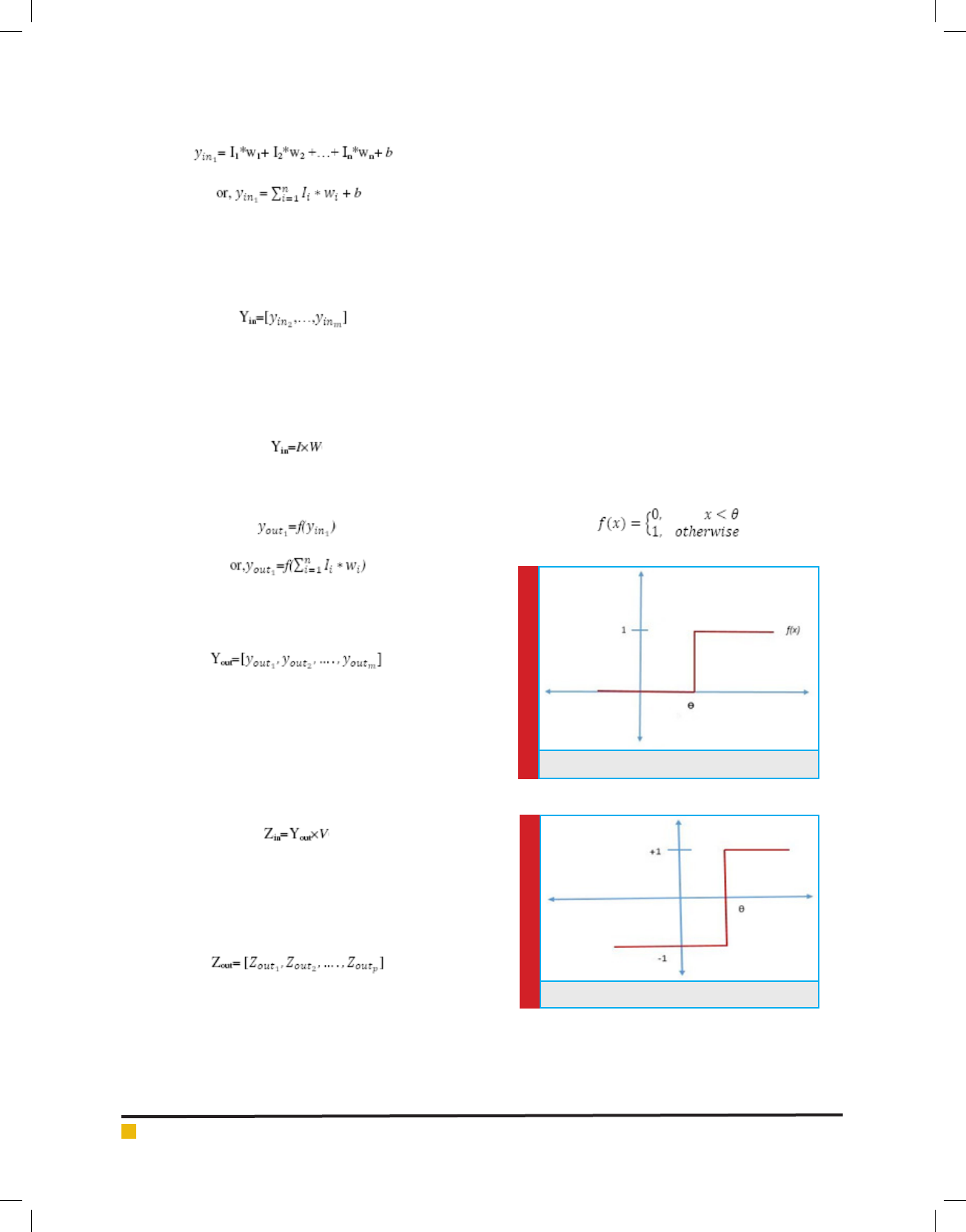
STEP FUNCTION

There are two types of step functions, the binary step

function,and the bipolar step function. The binary step

function produces 0 as the output if the net input is

less than the certain threshold value  otherwise, it pro-

duces 1 as the output.It can be represented mathemati-

cally as given in equation 10 and graphically as given in

 gure 3.

(1)

(2)

(3)

Let the inputs are represented in the form of the vector

as I = (I

, I

… , I

) and W is the matrix of weights associ-

ated with the interconnections between the input layer

and the hidden layer then Y

will be de ned as the cross

product of the input vector and the weight matrix, i.e.,

(4)

If f is the activation function used at this neuron, then

the output of the neuron is obtained as:

(5)

Similarly, the output generated by all the neurons of the

hidden layer can be represented in the form of a vector

as:

(6)

(7)

Now, this output Y

out

is supplied as input to each neuron

of the output layer. Let V is the matrix of weights associ-

ated with the interconnections between the hidden layer

and the output layer then the input received at output

layer will be the cross product of Y

out

and V. Let Z

is the

net input received at output layer, then it can be repre-

sented as:

(8)

Let is the output generated by each of the i

neuron at

output layer and there are p number of nodes are there

at this layer, then the net output collected at output layer

can be represented as the vector of outputs generated by

each neuron. It can be given as:

(9)

ACTIVATION FUNCTIONS

Every neuron in the neural network generates the out-

put which is referred as the activation of the neuron.

Initially, when the neurons are not generating any out-

put are said to be not activated. When the applied input

(10)

FIGURE 3. Binary Step Function

FIGURE 4. Bipolar Step Function

The bipolar step function is used when the neural net-

work is to be applied to bipolar data instead of binary

data. This function gives -1 and + 1 as the output in

place of 0 and 1 depending on the threshold. This func-

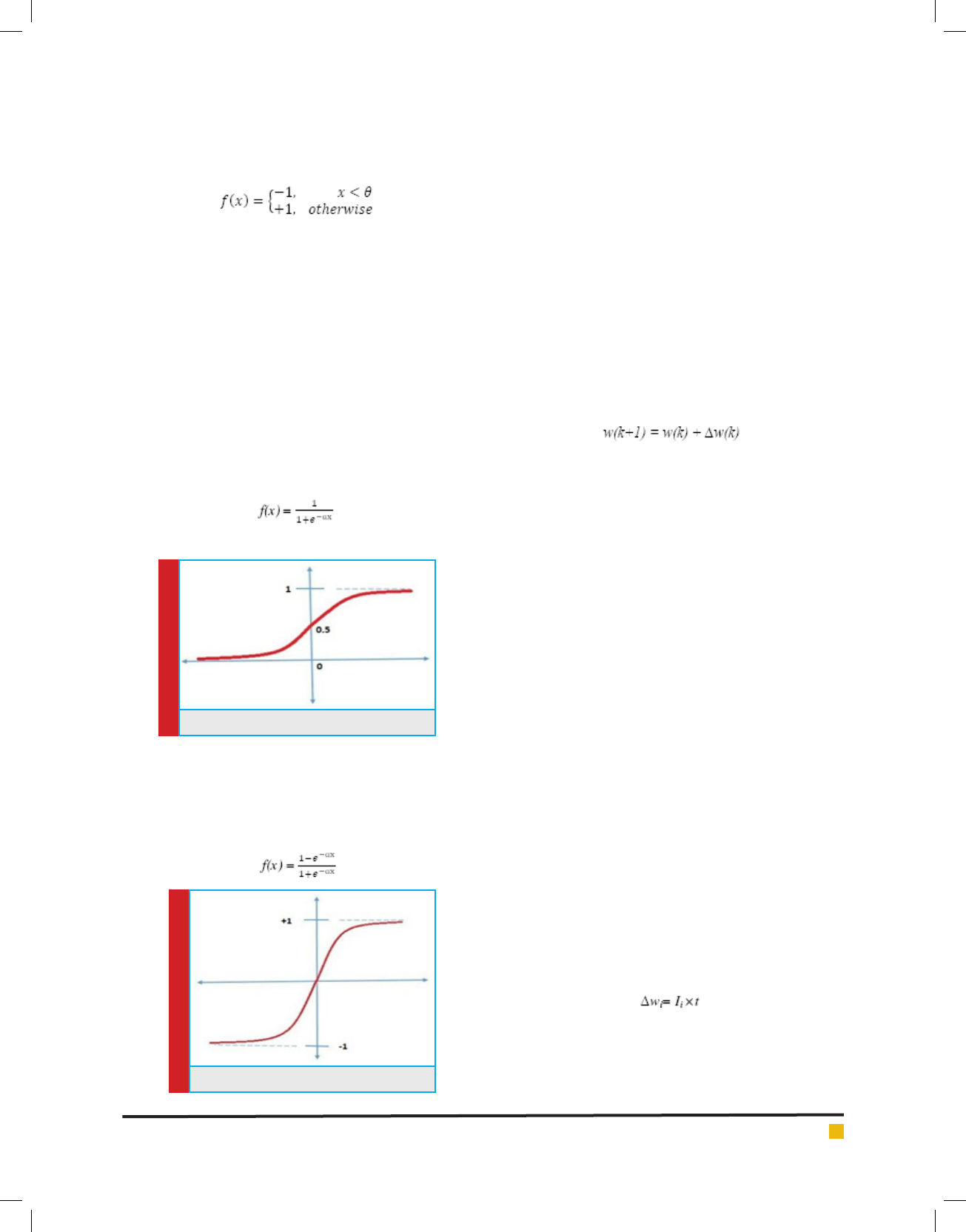
Nitesh Malhotra and Aksh Chahal

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS DEEP LEARNING TECHNIQUES AND THEIR APPLICATIONS 703

tion can be represented mathematically as given in

equation 11 and graphically as given in  gure 4.

LEARNING BY ANNS

An arti cial neural network has three important char-

acteristics, the architecture, the activation function and

the learning. The weights associated with the intercon-

nection between neurons of the network are initialized

randomly before training of the network. These weights

are adjusted by following the learning algorithm and

when  nalized, the network is said to be a stable of the

 tted network. A network  tted after training can be

applied to a problem (Haykin, 1998). During training,

the weights of the neural network are updated at each

iteration of the training until some stopping condition

is satis ed. Let w(k) is the weight at k

iteration of the

training then the new weight at (k+1)

is obtained as

given in the equation 14.

(11)

SIGMOID FUNCTION

Since the step functions are not continuous, so they

are not differentiable. There are some machine learning

algorithms which require the continuous and differenti-

able activation functions and hence the step functions

cannot be used in those problems. The sigmoid functions

can be approximated with maintaining their property of

differentiability. There are two types of sigmoid func-

tions used in this type of problem domain, the binary

sigmoid function,and the bipolar sigmoid function. They

both have the continuous outputs.

The binary sigmoid function is also called the logistic

sigmoid function. It can be represented mathematically as

given in equation 12 and graphically as given in  gure 5.

(12)

FIGURE 5. Binary Sigmoid Function

where  is called the steepness parameter.

The binary sigmoid function has the limitation that it

cannot be applied to bipolar data. In this case, the bipo-

lar sigmoid function is used for continuous output. It

can be represented mathematically as given in equation

13 and graphically as given in  gure 6.

FIGURE 6. Bipolar Sigmoid Function

(13)

(14)

where the Δw(k) is the change in weight w at k

itera-

tion. Different learning methods give a different method

to obtain the Δw(k).

There are various learning methods used by neural

networks which are categorized mainly into two catego-

ries, the supervised learning and the unsupervised learn-

ing (Jain et al, 1996).

SUPERVISED LEARNING

The supervised learning methods work with the labeled

data. Labeled data means the data where there are input

and output labels given in the data. The training data for

a neural network is referred as the training pattern. Each

training pattern consists of the input patterns and cor-

responding output patterns in case of supervised learn-

ing. The learning algorithms devise a function mapping

between the input and output patterns of the data. Once

the network is trained by following the learning algo-

rithm, it can generate output for an unknown input pat-

tern (Reed et al, 1999). Here we will present a very brief

description of the supervised learning algorithms popu-

larly used in the training of neural networks.

HEBB RULE

It is one of the earliest learning algorithms used by

the arti cial neural networks. According the Hebb rule

or Hebbian learning, the change in weight w

can be

obtained as:

(15)

where I

is the corresponding input value and the t is

the target value. The Hebb rule has the limitation that it

cannot learn if the target is 0. This is because the change

in weight Δw

will become 0 when we put t=0. So it is

Nitesh Malhotra and Aksh Chahal

704 DEEP LEARNING TECHNIQUES AND THEIR APPLICATIONS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

applied when the input and output both are in bipolar

form (Kempter et al, 1999).

PERCEPTRON LEARNING RULE

According to the perceptron learning, if the output of

the neuron is not equal to the target output, then only

the weights associated with the interconnections should

be adjusted otherwise they should not be altered (Ng

et al, 1997). According to this rule, the change in weight

is obtained as:

network gives the output response indicating the cluster

to which the input vector belongs.The popular unsuper-

vised learning algorithm used for clustering using neural

network is Winner-Takes-All method. It is a competitive

learning rule which chooses the neuron with the greatest

total input as a winner (Kaski et al, 1994).

DEEP LEARNING MODELS

There are various deep learning models developed by the

researchers and they are applied in a different problem

domain. In all the models, the common characteristic is

the multiple layers of learning. Here in this section, we

will present a short survey of popularly used deep learn-

ing models.

DEEP NEURAL NETWORK

Deep neural network is a variant of multilayer feed-

forward arti cial neural network. It has more than one

hidden layers between the input layer and the output

layer (Bengio, 2009). The number of neurons are simi-

lar in each of the hidden layer. Initially, the number of

neurons are  xed randomly and it is adjusted manually

during training of the network. Larger the number of

nodes at hidden layer may result in an increase in the

complexity and hence the decrease in the training per-

formance. So, the selection of number of nodes at this

layer is carefully considered. This architecture devises a

compositional model in which the object is referred as

the layered composition of primitives. It has the capa-

bility to model complex non-linear relationships in the

training data. The bene t of using extra hidden layers

in the network enables the composition of features from

lower layers. These features potentially model complex

data with fewer units (Ngiam et al, 2011).

There are two issues also associated with the deep

neural networks. First, the issue of over tting which is

common in many neural network models and second,

the issue of computation time. The problem of over t-

ting has more chances to arise in deep neural network

due to the use of extra layers. Due to this issue, it mod-

els the rare dependencies in the training data. The net-

work gives better result on training data and degraded in

accuracy on validation data. To avoid the issue of over-

 tting in deep neural networks, regularization methods

like weight decay or sparsity can be used during train-

ing which excludes the modeling of rare dependencies.

With the increase in smaller training sets can also over-

come the problem of over tting. The computation time

of the learning model depends on many parameters like

such as the layer size, the learning rate, and the ini-

tially chosen weights (Szegedy et al 2013). The number

of nodes in the hidden layers increase the complexity of

the system and it requires more computational time. It

(16)

where  is a constant and known as the learning rate.

DELTA RULE

The Delta rule is also known as the Least Mean Square

(LMS) or Widrow-Hoff rule. It is a widely used learning

method used in the training of neural networks. It pro-

duces the output in binary form by reducing the mean

squared error between the activation and the target

value (Auer et al, 2018). According to the Delta rule, the

change in weight Δw

is obtained as:

(16)

where the symbols used have their usual meaning.

THE BACKPROPAGATION ALGORITHM

The backpropagation is the most popular learning algo-

rithm used for training the arti cial neural network in

case of supervised learning. In this algorithms, the neu-

ral net repeatedly adjusts the interconnection weights on

the basis of error and deviation from the target output

in response to the training patterns. The error in this

method is calculated at the output layer of the network

and propagated back through the network layers (Adeli

et al, 1994). We will discuss this method in detail in

chapter 6 while discussing the training of Hybrid Deep

Neural Network.

UNSUPERVISED LEARNING

When the training data available for training the neural

network does not has the input-output labels, the learn-

ing performed on this data is called the unsupervised

learning. In this case, the algorithms learns to derive

structure from the data. There are many machine learn-

ing problems like clustering and anomaly detection use

unsupervised learning (Hastie et al, 2008). In cluster-

ing problems, during training of the neural network, the

input vectors which are to be applied to the network are

combined to form clusters. When the network is trained

or stable, on applying a new input vector, the neural

Vaibhav Kumar and M L Garg

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS DEEP LEARNING TECHNIQUES AND THEIR APPLICATIONS 705

should be carefully considered while selecting all these

parameters.

A typical architecture of the deep neural network is

represented in  gure 7.

height and the width which are presented in one of the

layers. The 3D input volume is transformed to 3D out-

put volume of neuron activations by every layer of the

network. A typical architecture of convolutional neural

networks consist of the following:-

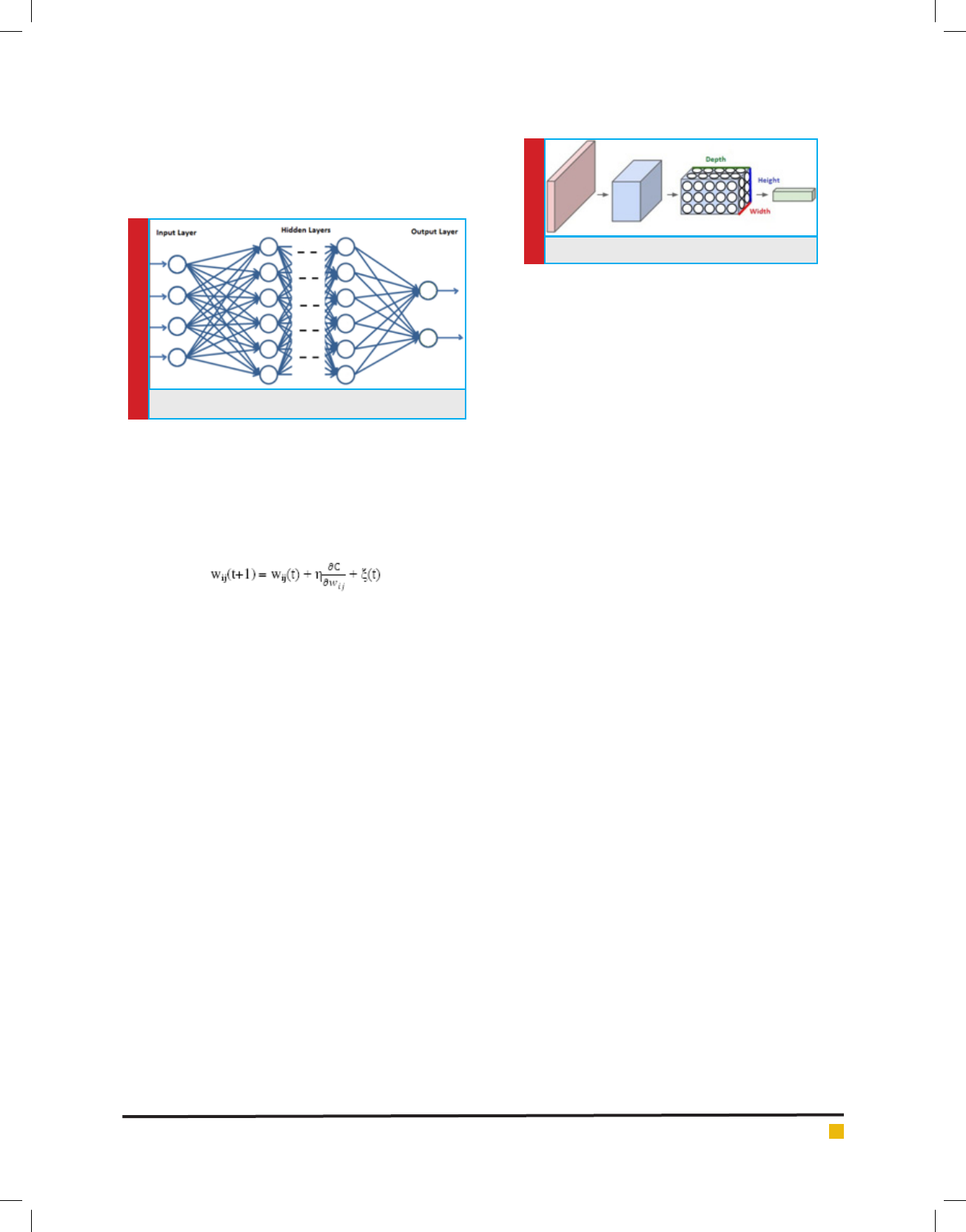
(i). Convolutional Layer: The convolutional layer of

the network is termed as the core building block which

comprises a set of learnable  lters. It is said that these

 lters are convolved around the layer. It applies a con-

volution operation to the input which is to be passed to

the next layer as a result of this operation. The network

learns from the  lters as they are activated after detect-

ing certain speci c type of features at certain spatial

input position.

(ii). Pooling Layer: Pooling layer helps the convolu-

tional neural network in avoiding the issue of over tting

which is a common issue in arti cial neural networks.

Pooling, which is a form of non-linear down-sampling,

combines the outputs of neurons of one layer into a sin-

gle neuron of next layer. The max-pooling partitions the

input data into a set of non-overlapping slices and pro-

duces the maximum output for each set.

(iii). Local Connectivity: In convolutional neural net-

works, neurons of one layer are connected only to the

neighboring neurons of adjacent layers. When dealing

with the input of high volume, this features avoids the

problem of connectivity and hence reduces the com-

plexity of the network.

(iv). Parameter Sharing: There is a feature of parameter

sharing in convolutional neural networks which helps in

controlling the free parameters. Weight vectors and bias

values are shared among the neurons of the network

which helps in less parameter optimization and faster

convergence during training.

In the  eld of natural language processing, convo-

lutional neural networks are applied to text analytics

and sentence classi cation problems (Kalchbrenner et al,

2014). Itis also used in the time-series analysis which

is helpful in predicting stock prices, heights of ocean

tides and weather (LeCun et al, 1998). The architecture

of convolutional neural network has been used in pre-

dicting the DNA sequence binding (Zeng et al, 2016).

These architectures are also used in drug discovery by

FIGURE 7. Deep Neural Network

All the processing in the deep neural network is very

much similar to the multilayer feed-forward arti cial

neural networks. For training of the network, the back-

propagation learning method is used widely to  nd the

matching between the actual output and the desired out-

put. The change in weight in this process is calculated

as:

(18)

where  is the learning rate, C is the cost function and

 is the stochastic term. w

is the weight associated with

the interconnection between i

node of one layer and j

node of next layer.

The deep neural networks have a wide range of

applications. They are applied in automatic speech rec-

ognition, image recognition, visual art processing, and

natural language processing, drug discovery, customer

relationship management, mobile advertising and many

more  elds.

CONVOLUTIONAL NEURAL NETWORK

The convolutional neural network is a variant of a mul-

tilayer perceptron. They are inspired by the biological

process of visualization. This model is a composition of

neurons, learnable weights, and bias values. It consists

of an input layer, an output layer and multiple hidden

layers between the input layer and the output layer.The

hidden layers of the network are the composition of the

convolution layers, pooling layers, fully connected lay-

ers and the normalization layers. They are designed in

such a manner that they require a minimal amount of

preprocessing (Aghdam, 2017, Krizhevsky et al 2012).

The architecture of a convolutional neural network is

represented in  gure 8 given below.

The architecture of convolutional neural network

comprises neurons in three dimensions, the depth, the

FIGURE 8. Convolutional Neural Network

Vaibhav Kumar and M L Garg

706 DEEP LEARNING TECHNIQUES AND THEIR APPLICATIONS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

predicting the interactions between biological proteins

and molecules (Strigl et al, 2010).

However convolutional neural networks have been

applied very usefully in many  elds and they have given

better results, some limitations are also associated with

this model. It requires a large data set and hence needs a

long training time. There is the issue of performance and

scalability also associated as this architecture is GPU

based (Hinton, 2009).

DEEP BELIEF NETWORKS

A deep belief network is a variant of the deep neural

network. It is a graphical model which is composed of

multiple layers of hidden units. The hidden units are

called the latent variables. There is an interconnection

between layers of the network but there is no connectiv-

ity among units of the network. This graphical model

learns to extract the deep hierarchical representation

of the training data (Hinton et al, 2006). The graphi-

cal model has both directed and undirected edges. The

training of the network is performed in two successive

steps, the unsupervised training and then thesupervised

training. During the unsupervised training, the network

learns to probabilistically reconstruct its inputs when

trained on a set of example. As a result of this training

step, the layers act as feature detectors. After this step,

the supervised training is performed on the network to

perform the task of classi cation (Salakhutdinov et al,

2007).

The deep belief network can be described by separat-

ing its architecture in two parts, the belief network,and

the Restricted Boltzmann Machine. The belief network

is a directed acyclic graphical model comprises the sto-

chastic variables. These variables have states either 0 or

1 where the probability of becoming 1 is obtained by a

bias and weighted inputs from other units. The belief

network solves two types of problems, the inference

problem,and the learning problem. The inference prob-

lem infers the state of the unobserved variables and the

learning problem adjusts the interconnection between

learning variables. This helps the network in generating

the observed data. The Restricted Boltzmann Machines

are the generative models of the arti cial neural net-

work which learns from the probability distribution of a

set of inputs (Larochelle et al, 2008).

A typical architecture of deep belief network is repre-

sented in  gure 9.

The deep belief network is composed of Restricted

Boltzmann Machine (RBM) and a feedforward multilayer

perceptron. The RBM is used at pre-training phase and

the multilayer perceptron is used at the  ne tune phase.

The hidden units of the network are the neurons which

cannot be observed directly but they can be inferred

from the other observable variables. In deep belief net-

works, the distribution between observed input vector X

and n

hidden layer h

is modeled as:

FIGURE 9. Deep Belief Network

(19)

where, X= h

, P (h

i-1

) is a conditional distribution of

visible units and P (h

n-1

) is the joint distribution for

visible units. During the  rst step of the training, the

network learns a layer of features from the visible units.

Then, in the next step, it treats the activation of previ-

ously trained feature as visible unit and learns features

in a second hidden layer. After following successive

steps in such manner, the whole network is said to be

trained when the learning for the  nal hidden layer is

achieved.

Deep Belief Networks have been used in  nancial

business predictions in order to empower the  nancial

industries. These networks have also been used in time

series prediction which then leads to  nancial market,

signal processing,and weather information prediction.

Draught has also been predicted by this model. It is also

used in predicting the quality of sound vehicle interior

noise (Medsker et al, 2001).

However, Deep Belief Networks have a wide range

of application, some limitations are also associated with

this model. Since deep belief networks are formed with

Boltzmann Machines, they have the limitation that when

the size of the machine is increased, the training time of

the model exponentially increased.

RECURRENT NEURAL NETWORKS

Recurrent neural network belongs to the class of arti -

cial neural network. In these networks, there is a directed

cyclic connection between its internal nodes along a

sequence. It exhibits the dynamic temporal behavior of

a time sequence. These networks use internal memory

states to process in the input sequences (Li et al 2015).

In conventional arti cial neural networks, input values

in an input vector are independent of eachother and

hence processed independently. But there are many tasks

Vaibhav Kumar and M L Garg

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS DEEP LEARNING TECHNIQUES AND THEIR APPLICATIONS 707

where the output is dependent on previous calculation

in a sequential process. The recurrent neural networks

are applied to such type of tasks where there is sequen-

tial process on inputs. This network is called recurrent

because it performs the same task for every element in

the sequence. The memory used by the network stores

the information about previous calculations. Practically,

these networks recall calculations of few previous steps

only (Schuster et al, 1997).

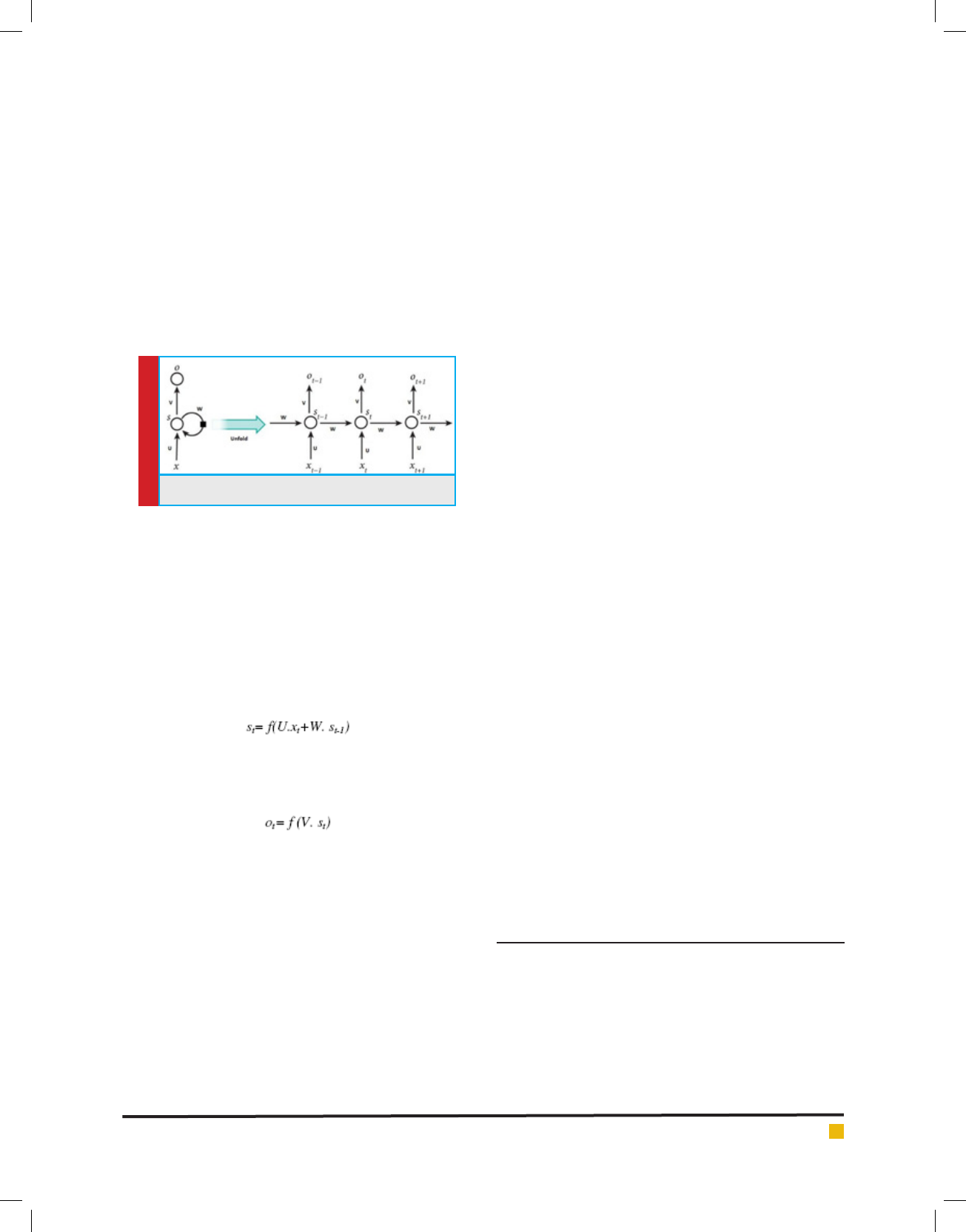
The working of the recurrent neural network can be

explained by the architecture represented in  gure 10

given below.

There are multiple extensions of the recurrent neural

network. They are discussed brie y as given below.

• Bidirectional Recurrent Neural Networks: This

network is based on the concept that the output

at t timestamp is not only dependent on the previ-

ous elements in the sequence but it also depends

on the future elements. It architecture is such as

two recurrent neural networks are stacked on top

of eachother. Its output is calculated based on the

hidden state of both networks (Irsoy et al, 2014).

• Deep Bidirectional Recurrent Neural Networks:

These networks are similar to the bidirectional

recurrent neural networks with an addition that

they have multiple layers per timestamp. It gives

the bene t of higher learning capacity but it needs

a large size of training data (Hochreiter et al, 1997).

• Long Short-Term Memory (LSTM) Networks:

This variant of the recurrent neural network is

applied to avoid the vanishing gradient problem in

backpropagation learning. In these networks, the

memory units are called as cells which are very

ef cient to capture long-term dependencies. It

takes the previous state s

t-1

and current input x

input to the cells and these cells decide internally

that which information will be stored and which

information will be erased (Saad et al, 1998).

Recurrent Neural Networks have a large number of

applications in predictive analytics. It has been widely

used in stock market predictions for a long period of

time (Connor et al 1994). Its application in time series

prediction has given the generalization of performance

than other models (Hu et al, 2007). These networks, after

combining dynamic weights, have been used to predict

the reliability of the software (Barbouniset al 2006).

With the addition of spatial correlation features, the

recurrent neural network is used to predict the speed of

wind (Levin, 1990).

Apart from the above important applications, RNNs

have some limitations. There is a slow training time of

these networks. In RNNs, number of hidden neurons must

be  xed before training. While processing a vocabulary,

size of context must be small (Sundermeyer et al, 2013).

CONCLUSION AND FUTURE SCOPE

In this paper, we have discussed the various techniques

used in deep learning applications. All these models have

an outstanding record in the area of machine learning.

There is a scope to create new features in these models

so that they can be applied in many domains with bet-

ter performance. The new techniques may be integrated

to exploit the opportunities of the model in prediction.

Parameter tuning can also help to improve the perfor-

FIGURE 10. Recurrent Neural Network

The above representation shows a recurrent neural

network being unfolded into a full network to process

a sequence of inputs. Here, one layer works for each

input value in the sequence. If folded or combined all

the layers together as a single hidden layer, the weights

and bias remain same because of only one hidden layer

is used in the network. Let x

is an input to the network

at timestamp t and s

is the hidden state or memory at

timestamp t. This s

is calculated on the basis of hid-

den state at previous timestamp and the input at current

timestamp as

(20)

where f is a nonlinear function which may be tanh or

ReLU. s

t-1

is initialized to zero at  rst timestamp. o

is the

output at t timestamp which is calculated as

(21)

in the above equation 4.21, f is a logistic function

which may be softmax or a normalized exponential

function.

Unlike the other deep neural networks where differ-

ent parameters like weights and bias are used at dif-

ferent hidden layers, in the recurrent neural network

these parameters are shared across all the timestamps.

This helps in reducing the number of parameters during

learning. In some applications, there is input required

at each timestamp and there is an output produced at

each timestamp. But it is not necessary in every applica-

tion of recurrent neural network. This because of the use

of hidden state which captures information about some

sequences.

Vaibhav Kumar and M L Garg

708 DEEP LEARNING TECHNIQUES AND THEIR APPLICATIONS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

mance of these models. Parameter tuning can also help

to improve the performance of these models. So it can

be said that there is a very wide opportunity and open

scope for this model.

REFERENCES

Abraham A (2005) Arti cial Neural Networks. Handbook of

Measuring System Design, Willey Online Library.

Adeli H and Hung S-L (1994) Machine learning: neural net-

works, genetic algorithms, and fuzzy systems. John Willey &

Sons.

Aghdam H H and Heravi E J (2017) Guide to convolutional

neural networks: a practical approach to traf c sign detection

and classi cation. Springer Publication.

Auer P, Burgsteiner H and Maass W (2018) A learning rule

for very simple universal approximators consisting of a single

layer of perceptrons in Neural Networks Vol. 21 Issue 5: Pages

786-795.

Barbounis T G, Theochairs J B, Alexiadis M C and Dokopoulos

P S (2006) Long-term wind speed and power forecasting using

local recurrent neural network models in IEEE Transactions on

Energy Conversion Vol. 21 Issue 1: Pages 273-284.

Bebis G and Georgiopoulos M (1994) Feed-forward neural net-

works in IEEE Potentials Vol. 13 Issue 4: Pages 27-31.

Bengio Y (2009) Learning Deep Architectures for AI in Foun-

dations and Trends in Machine Learning Vol. 2 Issue 1: Pages

1-127.

Buscema M (1998) Back Propagation Neural Networks in Sub-

stance Use & Misuse Vol. 33 Issue 2: Pages 233-270.

Chen X-W and Lin X (2014) Big Data Deep Learning: Chal-

lenges and Perspectives in IEEE Access Vol. 2.

Connor J T, Martin R D and Atlas L E (1994) Recurrent neural

networks and robust time series prediction in IEEE Transac-

tions on Neural Networks Vol. 5, Issue 2: Pages 240-254.

Deng L and Yu D (2014) Deep Learning: Methods and Applica-

tions in Fundamentals and Trends in Signal Processing, Vol. 7

Issue 3: Pages 197-387.

Garven M V and Bohte S (Accessed 2018) Arti cial Neural Net-

works as Models of Neural Information Processing. Frontiers

Research Topics, Online.

Goodfellow I, Bengio Y andCourville A (2016) Deep Learning.

MIT Press, Online.

Hastie T, Tibshirani R and Friedman J (2008) Unsupervised

Learning. The Elements of Statistical Learning Springer Series

in Statistics: Page 485-585.

Haykin S (1998) Neural Networks: A Comprehensive Founda-

tion. Prentice-Hall, 2

Edition.

Hinton G (2009) Deep Belief Networks in Scholarpedia, Vol.

4, Issue 5.

Hochreiter S and Schmidhuber J (1997) Long Short-Term

Memory in Neural Computation Vol. 9 Issue 8: Pages- 1735-

1780.

Hinton G E, Osindero S and Teh Y W (2006) A Fast Learning

Algorithm for Deep Belief Nets in Neural Computation Vol. 18

Issue 7: Pages 1527-1554.

Hoff R D (Accessed 2018) Deep Learning: A Breakthrough

Technology. MIT Technology Review, Online.

Hop eld J J (1988) Arti cial neural networks in IEEE Circuits

and Device Magazine Vol. 4 Issue 5: Pages 3-10.

Hu Q P, Xie M, Ng S H and Levitin G (2007) Robust recur-

rent neural network modelling for software fault detection and

correction prediction in Reliability Engineering and System

Safety Vol. 92 Issue 3: Pages 332-340.

Irsoy O and Cardie C (2014) Opinion Mining with Deep Recur-

rent Neural Networks in Proceedings of the 2014 Confer-

ence on Empirical Methods in Natural Language Processing

(EMNLP): Pages 720–728.

Jain A K, Mao J and Mohiuddin K K (1996) Arti cial neural

networks: a tutorial in Computer Vol. 29 Issue 3: Pages 31-44.

Kalchbrenner N, Grefenstette E andBlunsom P (2014) A Convo-

lutional Neural Network for Modelling Sentences in Proceed-

ings of the 52

Annual Meeting of the Association of Com-

putational Linguistics, Baltimore, Maryland: Pages 655-665.

Kaski S and Kohonen T (1994) Winner-take-all networks for

physiological models of competitive learning in Neural Net-

works Vol. 7 Issue 6: Pages 973-984.

Kempter R, Gerstner W and Hemmen J L (1999) Hebbian learn-

ing and spiking neurons in Physical Review E Vol. 59 Issue 4:

Pages 4498-4514.

Krizhevsky A, Sutskever I and Hinton G E (2012) ImageNet

Classi cation with Deep Convolutional Neural Networks in

Proceedings of Advances in Neural Information Processing

Systems 25.

Larochelle H and Bengio Y (2008) Classi cation using dis-

criminative restricted Boltzmann machines in Proceeding of

International Conference on Machine Learning, Finland:

Pages 536-543.

LeCun Y and Bengio Y (1998) Convolutional networks for

images, speech, and time series in The handbook of brain the-

ory and networks: Pages 255-258.

Levin E (1990) A recurrent neural network: Limitations and

training in Neural Networks Vol. 3 Issue 6: Pages 641-650.

Li X and Wu X (2015) Constructing long short-term memory

based deep recurrent neural networks for large vocabulary

speech recognition in Proceedings of the IEEE International

Conference on Acoustics, Speech and Signal Processing, QLD,

Australia.

Medsker L R and Jain L C (2001) Recurrent Neural Networks:

Design and Applications. CRC Press LLC.

Najafabadi M M, Villanustre F, Khoshgoftar T M, Seliya N,

Wald R and E Muharemagic (2015) Deep learning applications

and challenges in big data analytics in Journal of Big Data Vol.

2 Issue 1: Pages 1-21.

Ng H T, Goh W B and Low K L (1997) Feature selection, per-

ceptron learning, and a usability case study for text categori-

Vaibhav Kumar and M L Garg

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS DEEP LEARNING TECHNIQUES AND THEIR APPLICATIONS 709

zation in Proceedings of the 20th annual international ACM

SIGIR conference on Research and development in informa-

tion retrieval, Philadelphia, Pennsylvania, USA: Pages 67-

73.

Ngiam J, Khosla A, Kim M, Nam J, Lee H and Ng A (2011)

Multimodal Deep Learning in Proceedings of 28

International

Conference on Machine Learning, WA, USA.

Nisbet R, Miner G and Yale K (2018) Chapter-19, Deep Learn-

ing. Handbook of Statistical Analysis and Data Mining Appli-

cations, 2

Edition, Academic Press.

Reed R and Marks R J (1999) Neural Smithing: Supervised

Learning in Feedforward Arti cial Neural Networks. A Brad-

ford Book, MIT Press.

Roy S and Chakraborty U (2013) Introduction to Soft Comput-

ing: Neuro-Fuzzy and Genetic Algorithms. Pearson Education

India, 1

Edition.

Saad E W, Prokhorov D V and Wunsch D C (1998) Comparative

study of stock trend prediction using time delay, recurrent and

probabilistic neural networks in IEEE Transactions on Neural

Networks Vol. 9 Issue 6: Pages 1456-1470.

Salakhutdinov R, Mnih A and Hinton G (2007) Restricted

Boltzmann machines for collaborative  ltering in Proceeding

of 24

International Conference on Machine Learning, Oregon,

USA: Pages 791-798.

Schuster M and Paliwal K K (1997) Bidirectional recurrent neu-

ral networks in IEEE Transactions on Signal Processing, Vol.

45 Issue 11: Pages 2673-2681.

Strigl D, Ko er K and Podlipnig S (2010) Performance and

Scalability of GPU-based Convolutional Neural Networks in

Proceedings 18

Euromicro International Conference on Paral-

lel, Distributed and Network-Based Processing, Pisa, Italy.

Sundermeyer M, Oparin I, Gauvain J-L, Freiberg B, Schluter

R and Ney H (2013) Comparison of feedforward and recurrent

neural network language models in Proceedings of the IEEE

International Conference on Acoustics, Speech and Signal Pro-

cessing, BC, Canada.

Szegedy C, Toshev A and Erhan D (2013) Deep Neural Net-

works for Object Detection in Proceedings of the Advances in

Neural Information Processing Systems 26.

Yegnarayana B. Arti cial Neural Networks. Prentice-Hall of

India, Latest Edition.

Zeng H, Edwards M D, Liu G and Gifford D K (2016) Convolu-

tional neural network architectures for predicting DNA-protein

binding in Bioinformatics Vol. 32 Issue 12: Pages 121-127.