Biotechnological

Communication

Biosci. Biotech. Res. Comm. 11(2): 231-237 (2018)

A dynamic effect of infectious disease on prey predator

system and harvesting policy

Rachna Soni* and Usha Chouhan

Department of Mathematics, Maulana Azad National Institute of Technology Bhopal-462003, (M. P.) India

ABSTRACT

The paper deals with a model that describes a prey predator system with disease in the prey population where

we have investigated the effect of harvest on the disease when vaccination strategies fail to recover the infected

prey population. Many infectious diseases like varicella, which is a highly transferable infection caused by the

varicella zoster virus and causes even death if untreated. When the disease affected the prey species, prey species

is divided into two categories: susceptible prey and infected prey. From infected prey, the disease is transmitted

to the susceptible prey species. It is assumed that infection effect both prey and predator species, but the disease

is debilitating and ultimately causing death for predators. Once a predator is infected, it can be considered to be

dead and infected prey does not recover due to failure of vaccination strategies. The infected prey species are

subjected to harvesting at low and high harvesting rates. It is shown that effective harvesting of infected prey can

control the spread of disease and prevent predator species from extinction. Equilibrium points are obtained by lin-

earization and Jacobian matrix. The local and global stability of the various equilibrium points of the system was

investigated. It is observed that coexistence of both the prey and predator species is possible through non-periodic

solution due to the Bendixson-Dulac criterion. With the help of Routh-Hurwitz criterion and Liapunov function,

local and global stability of the non-periodic orbits are determined. Some numerical simulations have been carried

out to justify the results obtained.

KEY WORDS: PREY-PREDATOR MODEL, EQUILIBRIUM POINTS, STABILITY ANALYSIS, HARVESTING ACTIVITY

231

ARTICLE INFORMATION:

*Corresponding Author:

Received 25

March, 2018

Accepted after revision 26

June, 2018

BBRC Print ISSN: 0974-6455

Online ISSN: 2321-4007 CODEN: USA BBRCBA

Thomson Reuters ISI ESC / Clarivate Analytics USA and

Crossref Indexed Journal

NAAS Journal Score 2018: 4.31 SJIF 2017: 4.196

Online Contents Available at: http//www.bbrc.in/

DOI: 10.21786/bbrc/11.1/6

232 A DYNAMIC EFFECT OF INFECTIOUS DISEASE ON PREY PREDATOR SYSTEM AND HARVESTING POLICY BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Rachna Soni and Usha Chouhan

INTRODUCTION

Mathematical models have become important tools in

analyzing the dynamical relationship between predator

and their prey. The predator prey system is one of the

well-known models which have been studied and dis-

cussed a lot. The Lotka-Volterra predator prey system

has been proposed to describe the population dynam-

ics of two interacting species of a predator and its prey

(Lotka, 1925, Volterra, 1931, Arb Von et al., 2013),

Lotka–Volterra equation are of form

(1.1)

Where x and y are the prey and predator respectively; a

is the growth rate of the prey (species) in the absence of

interaction with the predator (species), b is the effect of

the predation of species to species, c is the growth rate

of species in perfect conditions: abundant prey and no

negative environmental impact and d is the death rate

of the species in perfect conditions: abundant prey and

no negative environmental impact from natural cause.

One of the unrealistic assumptions in the Lotka-Volt-

erra model is that the growth of the prey populations is

unbounded in the absence of the predator. Murray (Mur-

ray, 1989) modi ed the Lokta-Volterra model and the

model were based on assumptions that the prey popula-

tion exhibits logistic growth in the absence of predators,

then the model obtained:

(1.2)

where a, b, c, d, k

, k

are all positive constants. This

model was investigated and the conditions for stabil-

ity obtained.Ecological populations suffer from various

types of diseases. These diseases often play signi cant

roles in balancing the population sizes. Most impor-

tant models for the transmission of infectious diseases

descend from the classical SIR model (Kermack and

McKendrick,1927). In the past decades, several epidemic

models with disease in prey have been extensively stud-

ied in various forms and contexts, for example, by Heth-

cote, (2000), Hethcote et al., (2004), Johri et al., (2012),

Nandi et al., (2015), Sujatha et al., (2016), Mbava, (2017)

and Yang, (2018).

In particular, a predator-prey model with disease in

the prey and analyzed a model of a three species eco-epi-

demiological system, namely, susceptible prey, infected

prey and predator (Chattopadhyay and Arino,1999).

Another prey-predator model with harvesting activity of

prey which has been observed is that when the harvest-

ing activity of prey is taken into consideration, then the

population size of predator decreases and the naturally

stable equilibrium of the model becomes unstable (Singh

and Bhatti, 2012). A mathematical model to study the

response of a predator-prey model to a disease in both

the populations and harvesting of each species (Das,

2014), the model with two-stage infection in prey, the

early stage of infected prey is more vulnerable to preda-

tion by the predator and the later stage of infected pests

is not eaten by the predator (Nandi el al., 2015), har-

vested prey – predator model with SIS epidemic disease

in the prey population (Sujatha et al., 2016). The preda-

tor–prey model with disease in super-predator are inves-

tigated and obtained the results that in the absence of

additional mortality on predator by a super - predator,

the predator species survives extinction (Mbava, 2017).

A diffusive predator-prey model with herd behavior has

been developed and the local and global stability of the

unique homogeneous positive steady state is obtained

(Yang, 2018).

A compartmental mathematical model based on the

dynamics of the infection and apply vaccination strate-

gies with herd immunity to reduce the intensity of dis-

ease spread in the prey-predator ecosystem (Bakare et al.,

2012). We considered the work proposed by E.A. Bakare,

because sometimes vaccination strategies become inef-

fective, in that case dynamic changes developed in the

system, which we were investigated in the present work.

We are trying to demonstrate the effect of vaccination

when it failed to recover from the disease One of the

purposes of this article is to explore the complex effect

of the prey predator model in epidemiological system

due to failure of vaccination strategies. The proposed

model is characterized by a pair of  rst order nonlinear

differential equations and the existence of the possible

equilibrium points along with their stability is discussed.

And  nally, some numerical examples are discussed.

MATERRIAL AND METHODS

We shall consider the following prey predator system for

analyzing it mathematically,

(2.1)

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS A DYNAMIC EFFECT OF INFECTIOUS DISEASE ON PREY PREDATOR SYSTEM AND HARVESTING POLICY 233

Rachna Soni and Usha Chouhan

Where x, y and z stand for the density of susceptible

predator, susceptible prey andinfected prey populations,

respectively.And the parameters ‘a’ is the natural death

of the healthy susceptible predator, ‘b’ is the number

of contact between susceptible prey and healthy sus-

ceptible predator, ‘c’ is the number of contact between

healthy susceptible predator and infected prey, ‘e’ is the

number of contact between healthy susceptible predator

with infected prey and susceptible prey, ‘f’ is the number

of contact between healthy susceptible prey and infected

prey, ‘g’ is the harvesting rate of infected prey , h is the

per capita birth rate of susceptible prey (per time) and

infected prey and  is the proportion of those succes-

sively vaccinated at birth.

The model consists of basic assumptions that we

have made in formulating the model are: The relative

birth rate for infected prey and that of susceptible prey

remains the same.The disease is severely weakened

and ultimately causing death for the predators. Once a

predator is infected, it can be assumed to be dead. We

will therefore consider only susceptible predator andin-

fectious disease spreads among the prey population by

contact, and the rate of infection is proportional to the

infected and the susceptible prey.The predator makes no

difference between susceptible and infected members of

the prey population. The predator becomes infected by

consuming the infected prey. The rate of predator infec-

tion is proportional to the product of infected prey and

susceptible predators.The infected prey does not recover.

To begin with, let us  nd the equilibrium points of

the system (2.1)

The system (2.1) has the following equilibrium points:

Where x

, y

, z

are given by

In the next section, let us discuss the stability of the

 ve equilibrium points in the next which are obtained

above.

RESULTS AND DISCUSSION

Stability Analysis: In this section, we analyzed the local

behavior of the system (2.1) around each equilibrium

point. The Jacobian matrix of the system of state vari-

ables is as follows:

To determine the stability of the equilibrium points, we

look at the most useful techniques for analyzing non-

linear system is the linearized stability technique by

theorem1.

Theorem 1:

Let

There are at most three roots of the

equation

. Then the following statements are true:

a) If every root of the equation has absolute value

less than one, then the equilibrium point of

the system is locally asymptotically stable and

equilibrium point is called a sink.

b) If at-least one of the roots of the equation has

an absolute value greater than one, then the

equilibrium point of the system is unstable and

equilibrium point is called a saddle.

c) If every root of the equation has an absolute

value greater than one, then the system is

sourced.

d) The equilibrium point of the system is called

hyperbolic if no root of the equation has abso-

lute value equal to one. If there exists a root

of the equation with absolute value equal to

one, then the equilibrium point is called non-

hyperbolic (i.e. one eigenvalue has a vanishing

real part).

Let us preparefour propositions in order to discuss the

local stability around each equilibrium point.

Preposition 1: For system (2.1),

The equilibrium point E

is locally asymptotically stable

if h<1 and h<g.

Proof: The Jacobian matrix at E

(0,0,0) is given by

The Eigenvalue corresponding to the equilibrium point

(0,0,0) are –a, h, h-g. Only one Eigen value is negative

and other two depends upon the value of h i.e. Birth rate

of susceptible and infected prey. Then by theorem 1, we

obtain E

is locally asymptotically stable if h<1 and h<g.

Preposition 2: For system (2.1), The equilibrium point

E1is locally asymptotically stable if

and af+cg<1.

Proof: The Jacobian matrix at is given by

Rachna Soni and Usha Chouhan

234 A DYNAMIC EFFECT OF INFECTIOUS DISEASE ON PREY PREDATOR SYSTEM AND HARVESTING POLICY BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

If the corresponding Eigenvalues are 

, 

then

Thenby theorem 1, we obtain is locally

asymptoticallystable if and af+cg<1.

Preposition 3:For system (2.1),

The equilibrium point E

is locally asymptotically stable

if .

Proof: The Jacobian matrix at is given

If the corresponding Eigenvalues are 

, 

then

Then by theorem 1, we obtain is

locally asymptotically stable if and

Preposition 4:For system (2.1),

The equilibrium point E

is neutral if eigenvalue is imag-

inary.

Proof: The Jacobian matrix at

is given by

If the corresponding Eigenvalues are 

, 

then

One Eigen value l1 is negative if af<bg+af and the

remaining two Eigen values l2 and l3 are imaginary.

The Eigenvalues are purely imaginary, its real parts are

exactly 0. The equilibrium point is neutral.Then

by theorem 1(d), we obtain this preposition.

Let us discuss the stability of the E

by Routh-Hurwit-

zcriterian.Local stability of the system (2.1) around the

non-zero equilibrium point E

The Jacobian matrix at is given by

Where x*, y*, z* are given by

The characteristic polynomial for the Jacobian matrix

J (E

) is given by

Where

According to Routh-Hurwitzcriterian, is

asymptotically stable if and only if A

>0, A

>0 and

-A

>0.

Theorem 2. (E

) is globally stable.

Proof. Let a Liapunov function be,

The theorem above, then implies that (E

) is globally

asymptotically stable.

Now, let us  nd the global stability of the system

(2.1) around all the equilibrium points for different 2-D

planes by using Bendixson-Dulac criterion.

Theorem 3. E

is globally asymptotically stable in y-z

plane.

Proof. Let,

It is obvious that if and.

Now, we denote

Rachna Soni and Usha Chouhan

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS A DYNAMIC EFFECT OF INFECTIOUS DISEASE ON PREY PREDATOR SYSTEM AND HARVESTING POLICY 235

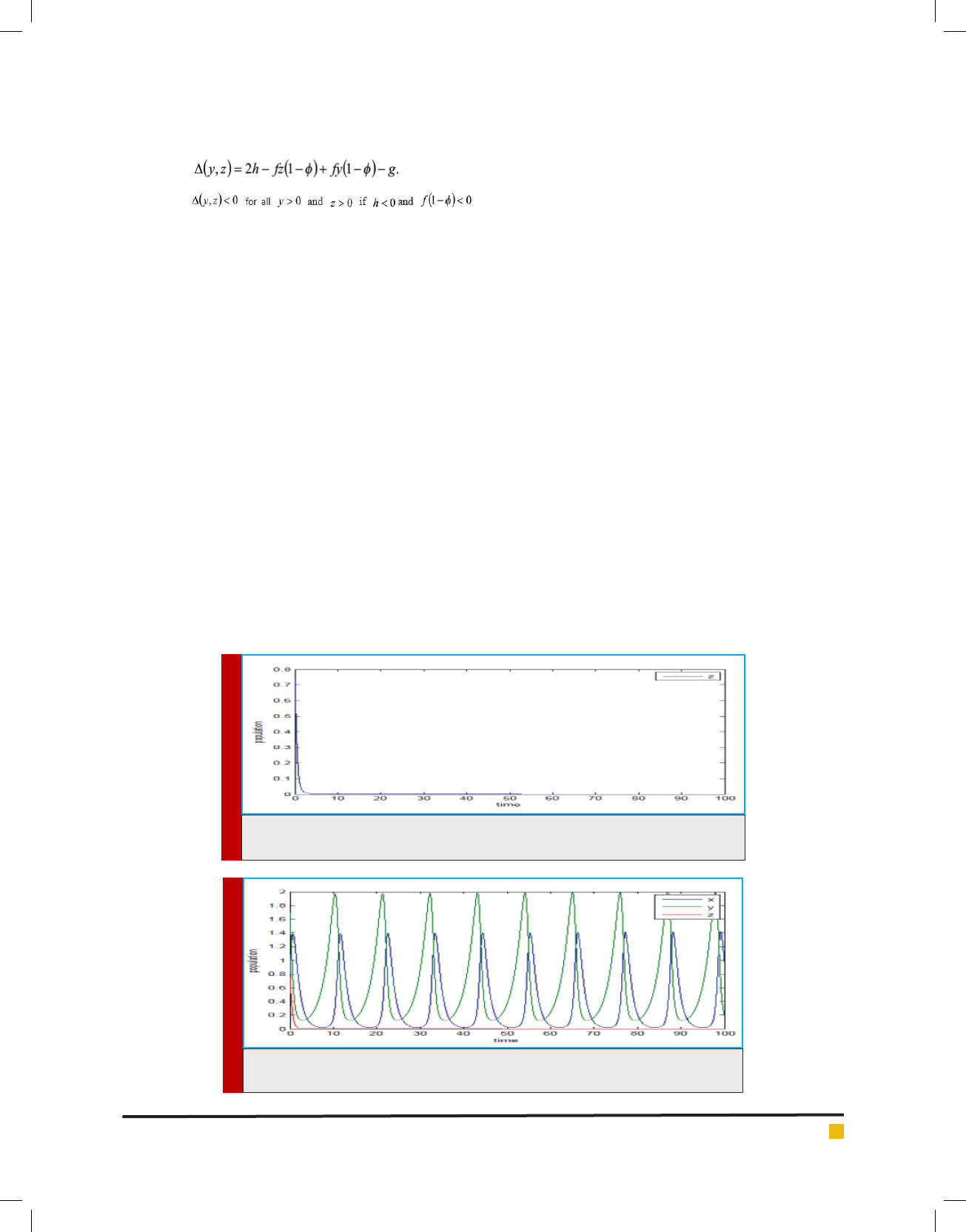
FIGURE 4a. Represents the effect of high harvesting on the population of the infected

prey as time goes on.

FIGURE 4b. Represents the effect of high harvesting on the population of the healthy

predator, susceptible prey and infected prey as time goes on.

Then,

Thus,

Therefore, by using Bendixson-Dulac criterion, there

will be no periodic orbit in the y-z plane.

In the similar manner, we can show in the x-z plane

for E1 with the condition x,z < 0 for all x > 0 and z

> 0 if h > 0, in the x-y plane for E

with the condition

x,z < 0 for all x > 0 and y > 0 if h,b < 0 and in the

same way E

can be globally asymptotically stable in

x-y,y-z and x-z planes.

We have performed some numerical simulation to

study the role of harvesting on the prey predator system

and we illustrate the dynamical and complex features of

the model using MATLAB. In the starting, we  xed all

parameters to ensure that the three classes of popula-

tions survive. Numerical simulations explain the effect

of the parameters on the complex behavior of a given

system (2.1).

(i) Let us consider following set of parameters,

a = 1.0; b = 1.5; c = 0.1; h = 0.5; e = 1.5;f=0.1;g=0.7,=0.91,

With initial condition x (0) =0. 8, y (0) =1. 70, z (0) =0.

75. For this set of parameter, we get the following vari-

ation of the population of the healthy predator, suscep-

tible prey and infected prey with respect to time, which

isillustrated below in  gure 4 (a) and  gure 4 (b).

(ii) Let us consider following set of parameters,

a = 1.0; b = 1.5; c = 0.1; h = 0.5; e = 1.5;f=0.1;g=0.1;=0.91;

With initial condition x (0) =0. 8, y (0) =1. 70, z (0) =0.

75. For this set of parameter, we get the following varia-

tion of the population of the healthy predator, suscepti-

ble prey and infected prey with respect to time, which is

illustrated below in  gure 4(c) and  gure 4(d).

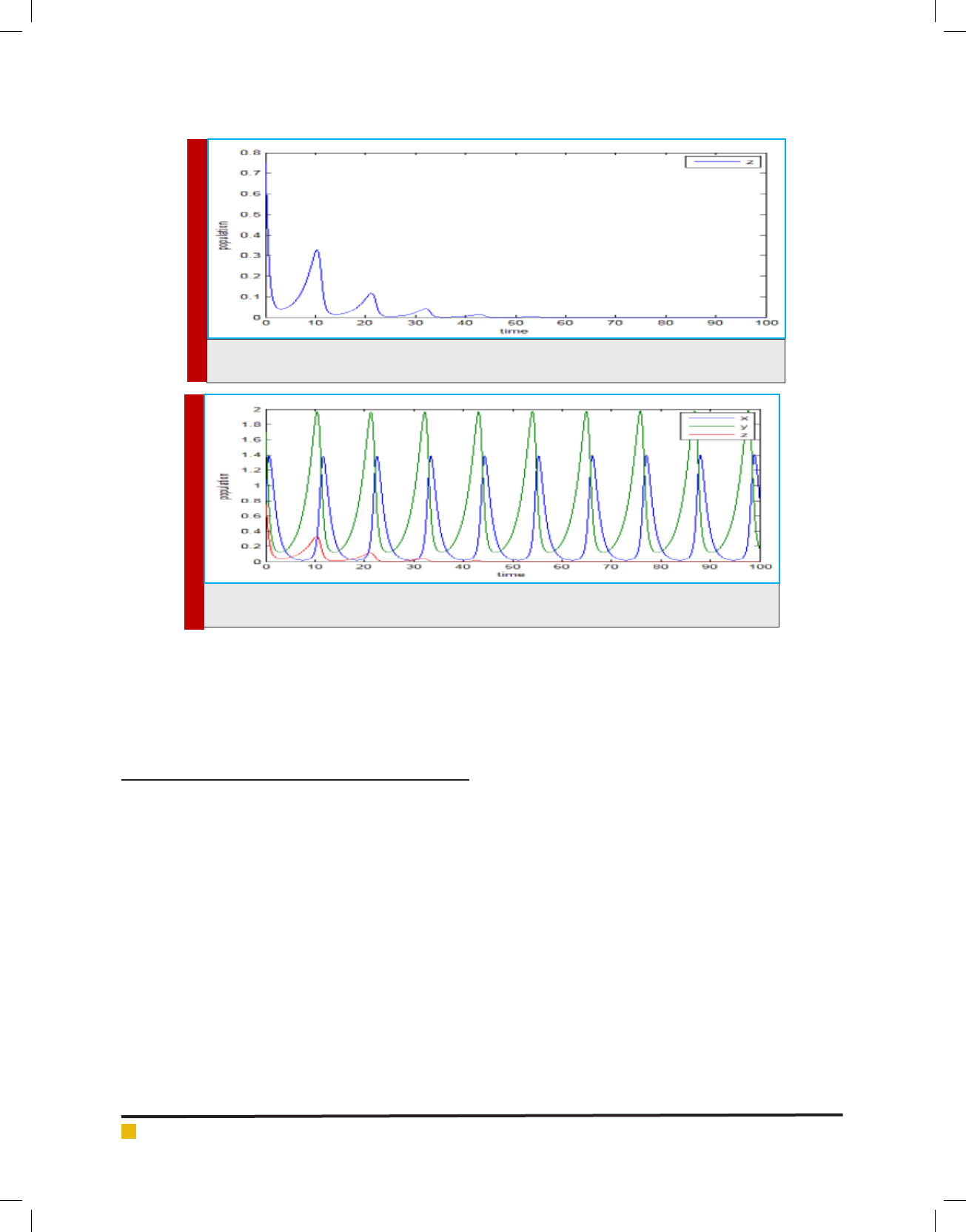
It is observed that effective harvesting of diseased

prey, increase the growth rate of the susceptible predator

population. If the value of harvesting rate g≥0. 7 then

the infected prey population decreases more rapidly,

but if the value of g<0.7 then infected prey population

decreases slowly that shown in  g. 4(a), 4(b), 4(c) and

4(d) respectively. In this analysis, we have also observed

that the whole population of the susceptible predators

may be wiped out due to increase in the number of the

susceptible and infected preys. This result shows that

the system is biologically well behaved. In another case

when the diseased prey can be washed out, a rational

use of the stability criterion of non-zero equilibrium

point may be useful for ecological balance. In this case,

the parameters of the system should be regulated in such

a way that stability criterion of non-zero equilibrium is

satis ed but infected prey remains low enough. Some-

Rachna Soni and Usha Chouhan

236 A DYNAMIC EFFECT OF INFECTIOUS DISEASE ON PREY PREDATOR SYSTEM AND HARVESTING POLICY BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

FIGURE 4c. Represents the effect of low harvesting on the population of the infected prey as time

goes on.

FIGURE 4d. Represents the effect of low harvesting on thepopulation of the healthy predator, suscep-

tible prey and infected prey as time goes on.

times, harvesting became a suitable option for preven-

tion of the population rather than the vaccination strate-

gies. Therefore, effective harvesting became essential for

the survival of the population.

CONCLUSION

A non-linear system based on the epidemic SIR model

has been studied and discussed. Conditions for local

and global stability at various equilibrium points were

obtained. We have illustrated the effective harvesting

of diseased prey in the whole system and reveal that

the increases of predator population when the harvest-

ing rate of infected prey population increases. We may

conclude that effective harvesting of diseased prey may

be used as a biological control for the spread of dis-

ease. And maintain balance in these species populations

by preventing in the predator population to extinction.

Finally, some numerical simulations illustrate and sup-

plement our theoretical analysis by considering different

parameter values. Low harvesting and high harvesting

rates play an important role in this analysis. Global sta-

bility of equilibrium E

shows that disease free equilib-

rium always exists. In future other effecting condition

can be used to save the predator population by introduc-

ing alternative food for predator rather than diseased

prey.

REFERENCES

Arb Von and Rachel (2013), Predator Prey Models in Competi-

tive Corporations,. Honors Program Projects, Paper 45.

Bakare E.A. et al. (2012), Mathematical Analysis of the Control

of the Spread of Infectious Disease in a Prey-Predator Ecosys-

tem, International Journal of Computer & Organization Trends

–Volume 2 Issue 1.

Chattopadhyay J. and Arino O. (1999), A predator–prey model

with disease in the prey, Nonlinear Analysis, Vol. 36, pp 747-766.

Das Krishna Pada (2014), Disease Control Through Harvesting

- Conclusion drawn from a mathematical study of a Predator-

Prey model with disease in both the population, International

Journal of Biomathematics and Systems Biology, Volume 1,

No. 1, pp 2394-7772.

E.A. Bakare Y.A Adekunle and A. Nwagwo (2012), Mathemati-

ca l Analysis of the Control of the Spread of Infectious Disease

in a Prey-Predator Ecosystem, International Journal of Com-

puter & Organization Trends –Volume 2 Issue 1.

Herbert W.et al. (2000), The Mathematics of Infectious Dis-

eases, SIAM Review, Vol. 42, No. 4., pp. 599-653.

Rachna Soni and Usha Chouhan

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS A DYNAMIC EFFECT OF INFECTIOUS DISEASE ON PREY PREDATOR SYSTEM AND HARVESTING POLICY 237

Hethcote HW et al. (2004), A predator–prey model with infected

prey, Theoretical Population Biology 66, pp 259–268.

Jia Yunfeng et al. (2017), Effect of predator cannibalism and

prey growth on the dynamic behavior for a predator-stage

structured population model with diffusion, J. Math. Anal.

Appl., 449, 1479–1501.

Jia Yunfeng (2018), Analysis on dynamics of a population

model with predator–prey-dependent functional response,

Applied Mathematics Letters,Vol. 80, 64-70.

Johri Atul et al. (2012), Study of a Prey-Predator Model with Dis-

eased Prey Int. J. Contemp. Math. Sciences,Vol. no. 10, 489–498.

Junej Nishant (2017), Effect of delay on globally stable prey–

predator system, Chaos, Solitons & Fractals, Vol. 111,146-156.

K. Sujatha et al. (2016), Dynamics in a Harvested Prey-Pred-

ator Model with Susceptible-Infected-Susceptible (SIS) Epi-

demic Disease in the Prey, Advances in Applied Mathematical

Biosciences, Volume 7, Number 1, pp. 23-31.

Kapur J.K., Mathematical Models in Biology and Medicine,

Published by Af liated East-West Press Private Limited, pages-

517.

Kermack W.O. and McKendrick A.G. (1927), A contribution to

the mathematical theory of epidemics, Proc. R. Soc. Lond, 115,

700-721.

Kooi B.W., Venturino E. (2016), Ecoepidemic predator–prey

model with feeding satiation, prey herd behavior and aban-

doned infected prey, Math. Biosci. 274, 58–72.

Lotka AJ. (1925), Elements of physical biology. Baltimore: Wil-

liams and Wilkins.

Mbava W. (2017) Prey, predator and super-predator model

with disease in the super-predator, Applied Mathematics and

Computation,Vol. 297, 92-114.

Murray J.D. (1989), Mathematical Biology, 2

, Edition.

Springer-Verlag, New York, 72-83.

Nandi Swapan Kumar and Mondal Prasanta Kumar (2015),

Prey-Predator Model with Two-Stage Infection in Prey: Con-

cerning Pest Control, Journal of Nonlinear Dynamics, Vol.15,

13 pages.

Pan Shuxia (2017), Invasion speed of apredator–preysystem,

Applied Mathematics Letters,Vol. 74, 46-51.

Singh Harkaran and Bhatti H.S. (2012), Stability of prey-

predator model with harvesting activity of prey, International

journal of pure and applied mathematics, volume 80 no. 5,

627-633.

Tang X. et al, (2015), Bifurcation analysis and turing instabil-

ity in a diffusive predator-prey model with herd behavior and

hyperbolic mortality, Chaos Solitons Fract. 81, 303–314.

Volterra V. (1931), Variations and  uctuations of a number

of individuals in animal species living together, Newyork:

McgrawHill, p. 409–48.

Yang Wenbin (2018), Analysis on existence of bifurcation solu-

tions for apredator-preymodel with herd behavior, Applied

Mathematical Modelling,Vol. 53, 433-446.