Biotechnological

Communication

Biosci. Biotech. Res. Comm. 10(2): 25-31 (2017)

An ef cient density-based algorithm for clustering

gene expressions

Prateek A. Meshram and Pradeep Singh*

Department of Information Technology and and *Department of Computer Science and Technology NIT

Raipur, Raipur, Chhattisgarh, India

ABSTRACT

Clustering of genetic expression in accordance to delineation is very important. To explore co-systematizes gene

groups whose collective samples are equal to the expressions used is one of the major work of gene clustering. In this

regards, an ef cient modi ed clustering algorithm is proposed for gene expression clustering. This algorithm forms

the various samples of the data and groups into a number of clusters in accordance with their density. In order to

achieve better clustering, we employed parameter tuning using differential evolution. The gene-gene class relevance

is being optimized by differential evolution to  nd the ef cient clusters. The performance of the algorithm is calcu-

lated with the study of some gene expression datasets and the validity measures. The proposed clustering algorithm

has outperformed when compared to the average linkage method, Self-Organizing Map (SOM) and a recently devel-

oped weighted Chinese restaurant-based clustering method (CRC), for clustering gene expression data.

KEY WORDS: CLUSTERING, GENE CLUSTERING, MUTUAL INFORMATION, VALIDITY MEASURES

ARTICLE INFORMATION:

*Corresponding Author: psingh.cs@nitrr.ac.in

Received 17

April, 2017

Accepted after revision 27

June, 2017

BBRC Print ISSN: 0974-6455

Online ISSN: 2321-4007 CODEN: USA BBRCBA

Thomson Reuters ISI ESC and Crossref Indexed Journal

NAAS Journal Score 2017: 4.31 Cosmos IF : 4.006

reserved.

Online Contents Available at: http//www.bbrc.in/

INTRODUCTION

The advancement of biological data analysis has made

the study of gene expression data faster and more ef -

cient. Biotechnology and intelligent informatics helped

in extraction of knowledge form collection of a very

large number of gene expressions of different times

and conditions (Meagher 2002), (Searls 2000). Extract-

ing patterns fromlarge amount of data is always a

great problem and clustering is the primary solution.

Clustering is an unsupervised learning process which

divides the data into number of sample spaces N regions

{C1,C2,…,CN} regards to speci c similarity or dissimi-

larity parameter, where N is unknown (Bandyopadhyay

et al. 2007). The main aim in partitional clustering is to

obtain a N×m matrix U(Y) of a given data Y, having

26 AN EFFICIENT DENSITY-BASED ALGORITHM FOR CLUSTERING GENE EXPRESSIONS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Prateek A. Meshram and Pradeep Singh

m objects, Y={y1,y2,…,ym}. To identify groups of co-

regulated genes groups clustering is extensively used on

gene expression data. Different unsupervised clustering

techniques such as hierarchical clustering (Herrero et al.

2001) (Wang et al. 2007) k-means algorithm (Heyer et al.

1999), self-organizing map (Wang et al. 2007)(Tamayo

et al. 1999), and principal component analysis (Yeung &

Ruzzo 2001)have been widely used to  nd patterns of

genes from microarray data. The hierarchical clustering

identi es sets of correlated genes with similar behavior

across the samples, but clusters in a tree-like structure,

which makes the identi cation of functional groups very

dif cult (Herrero et al. 2001) (Wang et al. 2007).

In contrast, self-organizing map (Heyer et al. 1999

and Tamayo et al. 1999) and k-means algorithm (Heyer

et al. 1999) require a prespeci ed number and an ini-

tial spatial structure of clusters, but this may be hard

to come up with in real problems. However, these algo-

rithms usually fail to reveal functional groups of genes

that are of special interest in sample classi cation as the

genes are clustered by similarity only, without using any

information about the sample categories or class labels

(Dettling & Bühlmann 2002) (Ben-Dor Shamir 1999).

Clustering conglomerates the like input patterns to de -

nite, and similar subsets having mutual inclusion are

termed as clusters (Xiao et al. 2003). Genes with identi-

cal changes in expressions are kept into separate clusters

in order to perform genome clustering. By considering

a mapping schemewe appoint a label to every gene and

the motive of clustering is applicable to this mapping

scheme i.e. to assign each gene to a speci c group.

There has been a signi cant growth in research in the

last decades of clustering and various clustering tech-

nologies have been developed, (Li & Tian 2007, Naka-

mura & Kehtarnavaz 1998, Frossyniotis et al. 2004) . Due

to the special characteristics of the gene data a special

study is dedicated to the genome data clustering.Density

Based Spatial Clustering Applications with noise is the

most used clustering algorithm for density clustering. By

giving a certain density threshold the linked regions are

identi ed with respect to the threshold. Density based

hierarchical clustering algorithm (DHC) using time series

proposed by Jiang in 2003 (Jiang & Zhang 2003). A new

version of K-means was developed by Barigov and Mar-

daneh, called an incremental algorithm for gene clus-

tering (Bagirov & Mardaneh 2006). Another technique

using K-means was proposed and given the name GAGR

(Chang et al. 2009). Zhihua in 2008 proposed a vari-

ant of PSO particle swarm optimization called PK-means

by combining the two techniques K-means and the

particle–pair optimizer in order to cluster the GE data

(Bagirov & Mardaneh 2006). GO Fuzzy a semi-super-

vised technique proposed by Tari in 2009 (Bagirov &

Mardaneh 2006). Juan A Nepomuceno proposed a new

evolutionary clustering technique in 2011 to cluster gene

expression data name bi-clustering with the help of gene

correlation based searching techniques(Nepomuceno et

al. 2011). A hybridized fuzzy algorithm named HFCEF a

framework developed for detecting tumor data was pro-

posed by Zhiwen Yu in 2013 using biomolecular data

(Yu et al. 2013).

Yiyi Liu proposed a new technique in 2014 to iden-

tify cancer subtypes based expression datasets which

accessed gene network information to perform cluster-

ing (Liu et al. 2014). Shudong Huang proposed a spectral

clustering algorithm named SCCE spectral co-clustering

ensemble algorithm, in 2015 to apply multiple based co-

clustering algorithms on various datasets (Huang et al.

2015) on a single platform. Recently Xianxue Yu, pro-

posed a new technique in 2017 to cluster gene expression

cancerous datasets with the help of projective ensemble

clustering named PCE (Yu et al. 2017).

There are lot of clustering techniques but DBSCAN is

the most used clustering algorithm for large data than

other algorithms (Ester et al. 1996). Most of the tech-

niques mentioned above don’t meet the requirements of

ef cient clustering of gene data, due to the constantly

changing characteristics of the microarray data. Con-

sidering all these issues, we propose, here, an ef cient

DBSCAN method which provides better genes groups

clustering. The rest of the paper is arranged as follows.

In Section 2, elaborates the Materials and Methods. The

Results and Discussion in Section 3. And Section 4 con-

cludes the paper.

MATERIAL AND METHODS

In this section, we have used 2 gene datasets and imple-

mented them using our new proposed algorithm with

the help of MATLAB 2016a. The implementation process

was carried onto Intel core i3 processor with 4GB RAM

and 500GB hard disk space, running on Windows 10

platform. The results obtained from the proposed algo-

rithm proved to be ef cient in terms of validity indexes.

Adjusted rand index (ARI) and Jaccard Index (JI) are

used as the main parameter for checking the ef ciency

of the algorithm. The value of the average of compact-

ness is varying between the range 0 to1 and the more

the value tends towards 0 the compactness leads to good

clustering and if the value of the average of compact-

ness tends to 1 the compactness leads to bad clustering

which is clari ed by the values of other measures.

GENE DATASETS

The gene datasets used in this paper are real life data set

namely yeast sporulation data and ratCNS central nerv-

ous system dataset.

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS AN EFFICIENT DENSITY-BASED ALGORITHM FOR CLUSTERING GENE EXPRESSIONS 27

Prateek A. Meshram and Pradeep Singh

Yeast Sporulation data: The dataset consists of sporu-

lation process genes of the budding yeast consisting of

6118 genes. The dataset is available on the following

website: http://cmgm.stanford. edu/pbrown/sporulation.

From the total 6118 genes, the genes which didn’t change

during the sporulation process are not considered. The

 nal set consists of 474 genes for the clustering.

RatCNS: The dataset consists of expression level of

the central nervous system development of rat which

consists of 112 genes over 9 time points. The data is

easily available on the following website: http://staff.

washington.edu/kayee/cluster. To obtain a good data for

clustering the dataset is normalized in such a manner

that each row is having mean 0 and variance 1(Ka Yee

Yeung, David R. Haynor n.d.).

DBSCAN is one of the most commonly clustering

algorithm based on a density-based notion of clusters,

DBSCAN is able to generate clusters of arbitrary shapes

ef ciently. DBSCAN accomplishes the clustering pro-

cess by starting from an arbitrary point X unvisited,

DBSCAN retrieves all points in the Eps neighbourhood

of X. Then try  nding all the density-reachable points

to the point X by considering the eps and minpts. If the

selected point is the core point then the cluster formation

is complete in according to the input parameters. Now

we check the border points by checking that no point is

density-reachable from the point X, which become a new

point and start again with the whole process. Even the

slightest of change in the values of the input parameters

can lead to the great changes in the clustering results.

As in the complete process of the DBSCAN algorithm, a

single point is visited multiple times, its time complex-

ity is O (N 2). By considering the density connectivity

and the density reachability we could easily determine

the working of DBSCAN. The values of both the density

functions depend on the two input parameters eps and

minpts where eps can be called as the radius de ned to

plot the cluster and the minpts are the minimum criteria

which are used to form a cluster. Finding the appropri-

ate value of eps and minpts is a challenging task. We

have introduced a new concept for getting the optimal

value of eps and minpts in ef cient way. The differential

evolution based parameter optimization for cluster com-

pactness improvement. The details of DE based param-

eter optimization is discussed below.

DIFFERENTIAL EVOLUTIONS

A new algorithm in evolutionary computing proposed

by Storn in 1977 for optimizing continuous spaces glob-

ally (Storn & Price 1997). The overall genetic algorithm

structure is in resemblance with (D.E.) Differential Evo-

lutions (Zou et al. 2013) (Marco Locatelli, Mirko Maisch-

berger 2014). Three basic operations such as mutation,

crossover, and selection are performed in DE. Mutation

is the most important operation in DE, its work is to

generate new population elements, in order to obtain

anoptimum solution in accordance with the objective

function (Yang Lou, Junli Li n.d.) (Chi 2009). In our sce-

nario we have used average compactness as the objec-

tive function as it is one of the suitable cluster validity

measure for density based clustering.

Time Complexity: Time complexity of the proposed

algorithm is where Iteration- is the number of DE itera-

tion. Population, number of individuals, complexity of

DBSCAN algorithm and n, number of data objects in the

datasets

For calculating the ef ciency of the algorithm we

have used validity indexes as the parameters for check-

ing its ef ciency, in it we used to adjust the Rand index,

Jaccard Index, Average of Compactness as the quality

measures of the proposed algorithm.

Average of Compactness

An internal measure based on the compactness of all

clusters which is used to measure the quality of cluster-

ing called as the average of compactness(Zaït & Mes-

satfa 1997). The lower value of average compactness

will provide the higher quality of clustering.

Adjusted Rand Index (ARI)

The adjusted Rand index is the corrected for chance ver-

sion of the Rand index(Rand & Rand 2016).Though the

Rand Index may only produce a value among 0 and +1,

the adjusted Rand index can produce negative values if

the index is less than the predictable index(Wagner &

Wagner 2007). If we have the result of clustering algo-

rithm R and the known classes L then the ARI can be

calculated in the following way. Let x, y, z and u be the

gene pairs in the same clusters related to both R and

L, clusters related to R and not L, clusters related to L,

not R and the clusters not related to both R and L. The

Adjusted Rand Index, is

(5)

Jaccard Index (JI)

The formula to calculate jaccard index is given below

it is a similarity measurement technique through which

we check the similarity between the expected(calculated)

and the actual number of clusters.

(6)

(IfAandBare both empty, we de neJ (A, B)=1.)

This distance is ametricon the collection of all  nite

sets (Lipkus 1999).

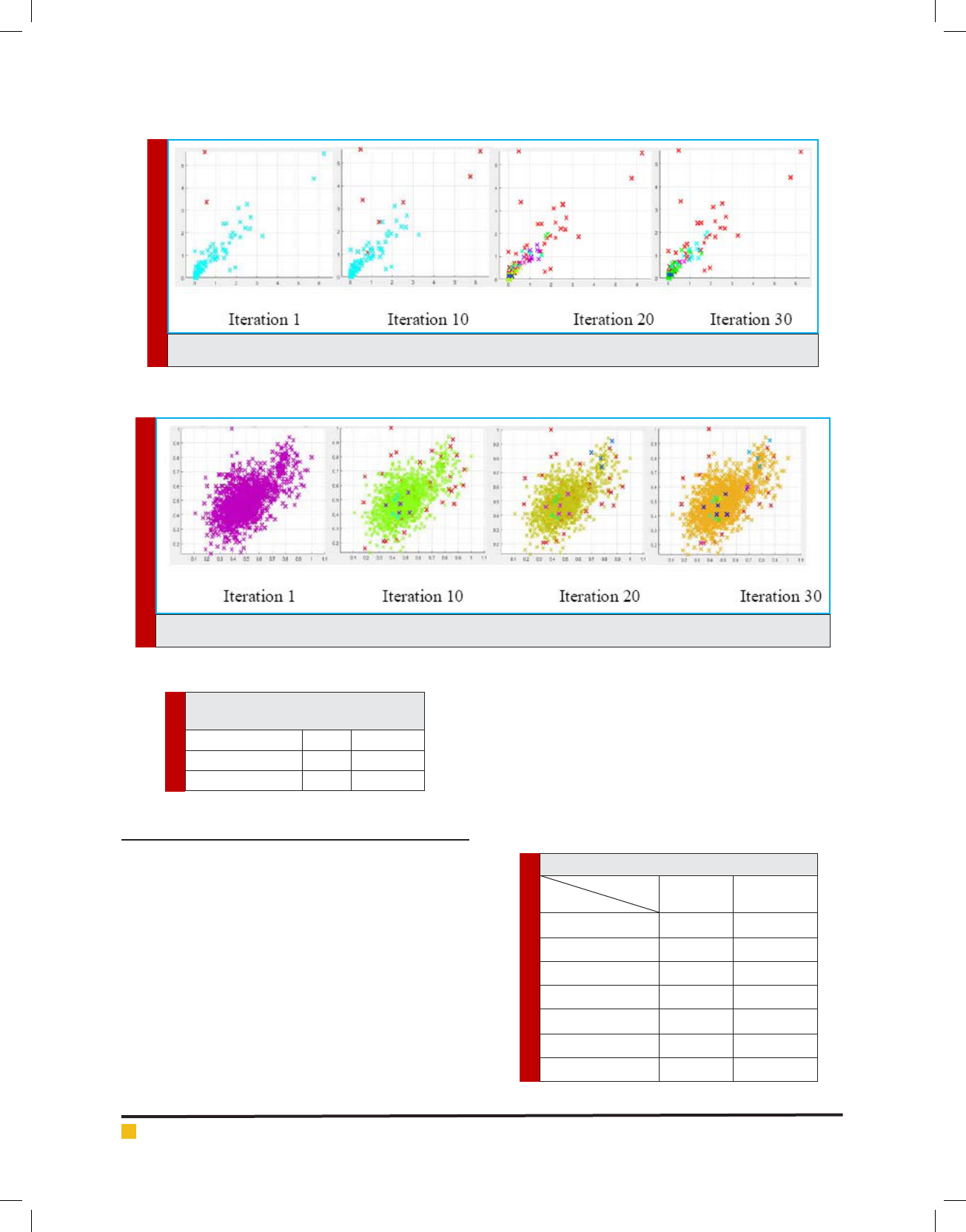
28 AN EFFICIENT DENSITY-BASED ALGORITHM FOR CLUSTERING GENE EXPRESSIONS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Prateek A. Meshram and Pradeep Singh

FIGURE 1. Variations in RatCNS dataset at various iterations.

FIGURE 2. Variations in Yeast dataset at various iterations.

Table 1. Number of clusters obtained by

the proposed algorithm

Yeast RatCNS

Original Clusters 10 6

Obtained Clusters 10 6

Table 2. Result of Proposed algorithm

Dataset

Algorithm

Yeast RatCNS

Our 0.9800 0.5560

SiMM-TS 0.6353 0.5147

IFCM 0.4717 0.4032

VGA 0.5800 0.4542

Average Link 0.5007 0.3684

SOM 0.5842 0.4134

CRC 0.5675 0.4455

 gure 2 shows the variations in the formation of clusters

in both the data sets at various iterations.

We compared our method with the previous algo-

rithms and results reported by Bandyopadhyay (Ban-

dyopadhyay et al. 2007) and found that the proposed

algorithm clusters more effectively than the previously

reported algorithms in terms of ARI. The observed values

for our algorithm on yeast gene expression is 0.9800 and

RESULTS AND DISCUSSION

In this section two datasets are implemented with our

proposed algorithm by optimizing the eps and minpts

with the objective function average of compactness

avg

). After getting the desired/ optimized value of the

minpts and eps we have used those parameters to get

the external measures such as ARI, and JI as the qual-

ity of measurement and to check the ef ciency of the

proposed system. The number of clusters formed by the

proposed algorithm is given in table 1 and it can be seen

that our proposed algorithm is identifying same number

of clusters in each dataset. The results of the proposed

algorithm with number of DE iterations are in terms of

average compactness is shown in table 2. Figure1 and

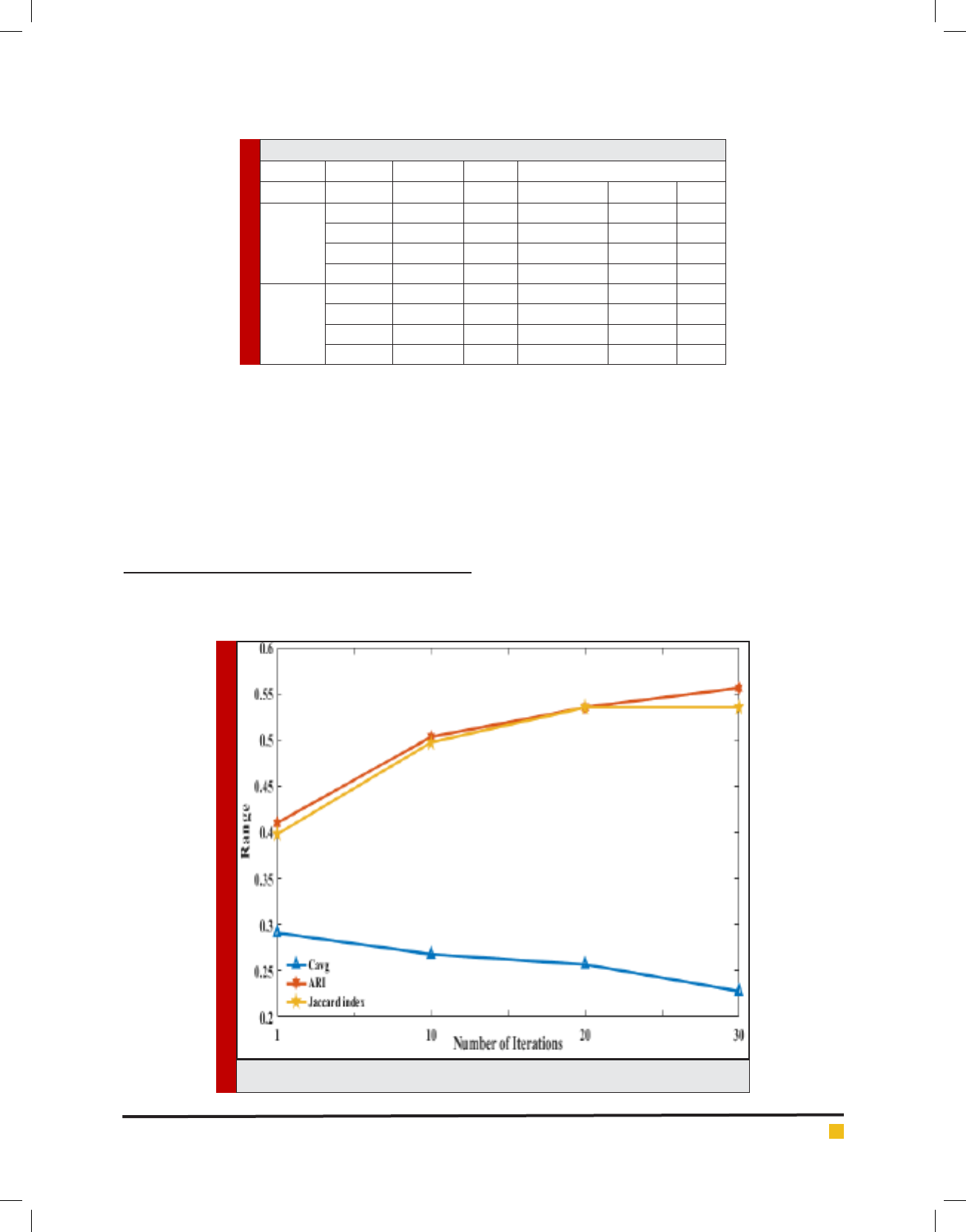
Prateek A. Meshram and Pradeep Singh

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS AN EFFICIENT DENSITY-BASED ALGORITHM FOR CLUSTERING GENE EXPRESSIONS 29

Table 3. Comparison of gene datasets for various algorithms with respect to ARI.

Dataset Eps Minpts Itr Proposed Algorithm

Cavg ARI JI

RatCNS

12.58 3 1 0.291 0.41 0.398

2.901 10 10 0.268 0.503 0.497

0.84 2 20 0.257 0.535 0.535

0.89 2 30 0.228 0.556 0.532

Yeast

29.46 5 1 0.200 0.222 0.222

0.198 4 10 0.123 0.775 0775

0.19 4 20 0.113 0.918 0.905

0.20 2 30 0.10 0.98 0.915

FIGURE 3. Variations in RatCNS dataset at different number of iterations.

on ratCNS is 0.5560 for ARI. The comparative results

vSiMM-TS, IFCM, VGA, Average Link SOM and CRC

are shown in table 3 .Figure 3 and Figure 4 shows the

graphical outputs of the indexes and the datasets with

respect to the number of iterations on validity indexes

ARI, JI and C

avg

respectively. Figure 5 shows the com-

parative graph with proposed method on the basis of

ARI index obtained from six algorithms.

CONCLUSION

A modi ed DBSACN which works without providing

the parameter eps and minpts is proposed in order to

reduce the complexity of the DBSCAN algorithm and

make it ef cient. The algorithm proposed is tested on

real life gene expression data sets. The results obtained

with the objective of minimization of average compact-

ness are compared to the existing algorithm in terms

of the ARI and JI validity measures. In general it is

found that the MDBSCAN clustering algorithm out-

performs all the other clustering methods signi cantly.

This algorithm provides the parameter optimization to

remove the major drawback of conventional DBSCAN.

Furthermore, we will study the selection of the auto-

matic parameter estimation model from the theoretical

aspect.

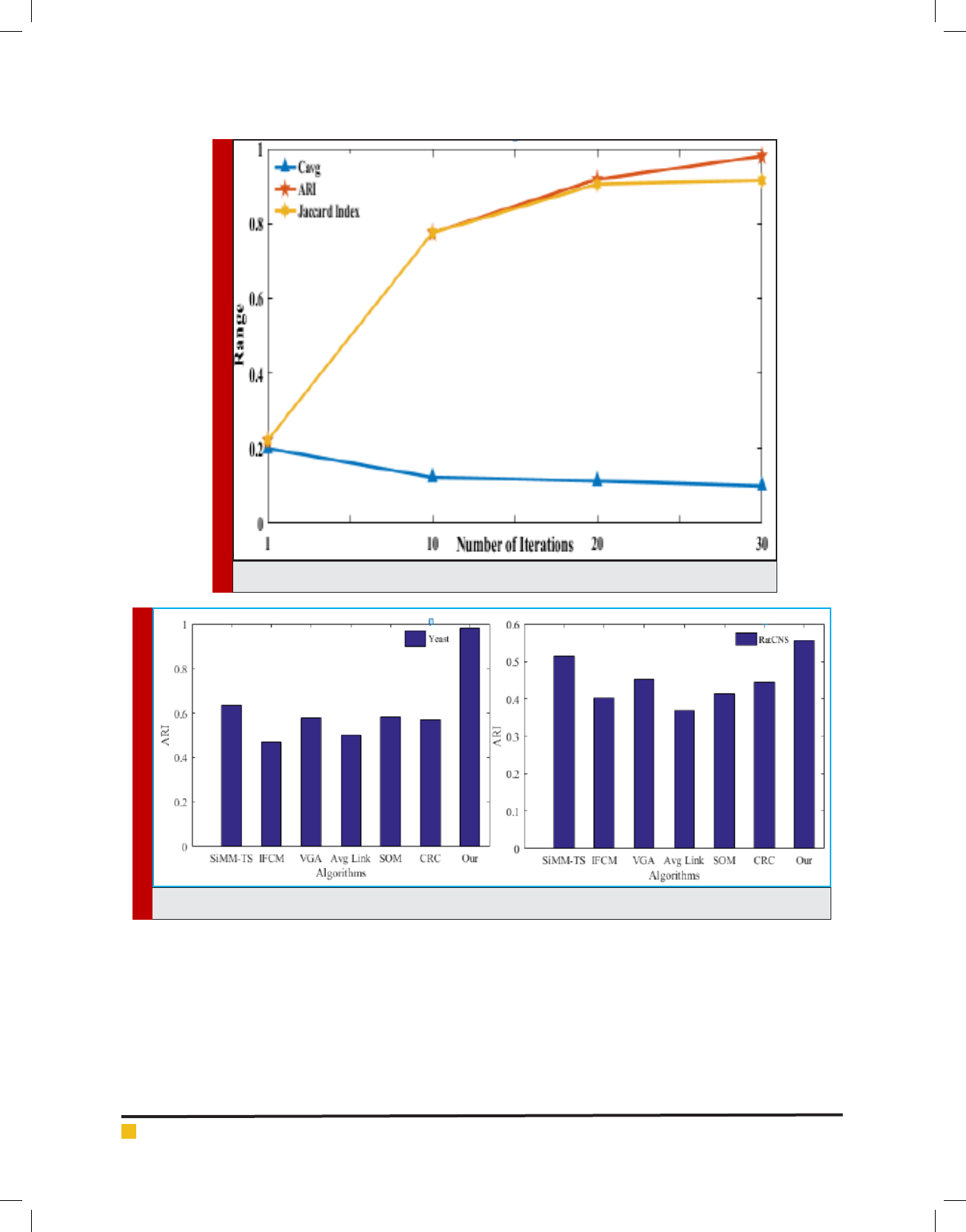
Prateek A. Meshram and Pradeep Singh

30 AN EFFICIENT DENSITY-BASED ALGORITHM FOR CLUSTERING GENE EXPRESSIONS BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

FIGURE 4. Variations in Yeast dataset at different intervals

FIGURE 5. Comparitive graph for the variations in the dataset with respect to ARI in all the algorithms compared.

REFERENCES

Bagirov, A. & Mardaneh, K., 2006. Modi ed global k-means

algorithm for clustering in gene expression data sets. Proceed-

ings of the 2006 workshop on, (4), pp.1–6. Available at: http://

portal.acm.org/citation.cfm?id=1274172.1274176.

Bandyopadhyay, S., Mukhopadhyay, A. & Maulik, U., 2007.

An improved algorithm for clustering gene expression data.

Bioinformatics, 23(21), pp.2859–2865.

Ben-Dor A, Shamir R, Y.Z., 1999. Clustering Gene Expression

Patterns. Computational Biology, 4, pp.281–97.

Chang, D.-X., Zhang, X.-D. & Zheng, C.-W., 2009. A genetic

algorithm with gene rearrangement for K-means clustering.

Pattern Recognition, 42, pp.1210–1222.

Chi, Y.A.; H., 2009. Experimental Study on Differential Evolu-

tion Strategies. IEEE Intelligent Systems, 2009. GCIS ’09. WRI

Global Congress on.

Prateek A. Meshram and Pradeep Singh

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS AN EFFICIENT DENSITY-BASED ALGORITHM FOR CLUSTERING GENE EXPRESSIONS 31

Dettling, M. & Bühlmann, P., 2002. Supervised clustering of

genes. Genome biology, 3(12), p.RESEARCH0069.

Ester, M. et al., 1996. A Density-Based Algorithm for Discover-

ing Clusters in Large Spatial Databases with Noise. Proceed-

ings of the 2nd International Conference on Knowledge Dis-

covery and Data Mining, pp.226–231.

Frossyniotis, D., Likas, A. & Stafylopatis, A., 2004. A clustering

method based on boosting. Pattern Recognition Letters, 25(6),

pp.641–654.

Herrero, J., Valencia, a & Dopazo, J., 2001. A hierarchical unsu-

pervised growing neural network for clustering gene expression

patterns. Bioinformatics (Oxford, England), 17(2), pp.126–136.

Heyer, L.J., Kruglyak, S. & Yooseph, S., 1999. Exploring

Expression Data : Identi cation and Analysis of Coexpressed

Genes Exploring Expression Data : Identi cation and Analysis

of Coexpressed Genes. , (213), pp.1106–1115.

Huang, S. et al., 2015. Spectral co-clustering ensemble. Knowl-

edge-Based Systems, 84, pp.46–55. Available at: http://dx.doi.

org/10.1016/j.knosys.2015.03.027.

Jiang, D. & Zhang, A., 2003. DHC: a density-based hierarchical

clustering method for time series gene expression data. Third

IEEE Symposium on Bioinformatics and Bioengineering, 2003.

Proceedings., pp.393–400. Available at: http://ieeexplore.ieee.

org/lpdocs/epic03/wrapper.htm?arnumber=1188978.

Ka Yee Yeung, David R. Haynor, W.L.R., Validating Clustering

for Gene Expression Data. Available at: http://staff.washing-

ton.edu/kayee/cluster.

Li, X. & Tian, Z., 2007. Optimum cut-based clustering. Signal

Processing, 87(11), pp.2491–2502.

Lipkus, A.H., 1999. A proof of the triangle inequality for the

Tanimoto distance. , 26, pp.263–265.

Liu, Y. et al., 2014. A network-assisted co-clustering algorithm

to discover cancer subtypes based on gene expression. BMC

bioinformatics, 15(1), p.37. Available at: http://www.biomed-

central.com/1471-2105/15/37.

Marco Locatelli, Mirko Maischberger, and F.S., 2014. No Title.

Differential evolution methods based on local searches. Com-

puters & Operations Research, 43:169–180, 2014.

Meagher, R.B., 2002. Post-genomics Networking of Biotech-

nology for Interpreting Gene Function. Current Opinion in

Plant Biology, 5(2), pp.135–140. Available at: http://dx.doi.

org/10.1016/S1369-5266(02)00245-5.

Nakamura, E. & Kehtarnavaz, N., 1998. Determining num-

ber of clusters and prototype locations via multi-scale clus-

tering. Pattern Recognition Letters, 19(14), pp.1265–1283.

Available at: http://www.sciencedirect.com/science/article/pii/

S0167865598000993.

Nepomuceno, J.A., Troncoso, A. & Aguilar-Ruiz, J.S., 2011.

Biclustering of gene expression data by correlation-based scat-

ter search. BioData mining, 4(1), p.3. Available at: http://www.

pubmedcentral.nih.gov/articlerender.fcgi?artid=3037342&tool

=pmcentrez&rendertype=abstract.

Rand, W.M. & Rand, W.M., 2016. Objective Criteria for the

Evaluation of Clustering Methods Objective Criteria for the

Evaluation of Clustering Methods. , 66(336), pp.846–850.

Searls, D.B., 2000. Using Bioinformatics in Gene and Drug Dis-

covery. Drug Discovery Today, 5(4), pp.135–143.

Storn, R. & Price, K., 1997. Differential Evolution – A Simple

and Ef cient Heuristic for global Optimization over Continu-

ous Spaces. Journal of Global Optimization, 11(4), pp.341–359.

Available at: http://dx.doi.org/10.1023/A:1008202821328.

Tamayo, P. et al., 1999. Interpreting patterns of gene expres-

sion with self-organizing maps: methods and application to

hematopoietic differentiation. Proceedings of the National

Academy of Sciences of the United States of America, 96(6),

pp.2907–2912.

Wagner, S. & Wagner, D., 2007. Comparing Clusterings - An

Overview. , (1907), pp.1–19.

Wang, H., Zheng, H. & Azuaje, F., 2007. Poisson-based self-

organizing feature maps and hierarchical clustering for serial

analysis of gene expression data. IEEE/ACM transactions on

computational biology and bioinformatics / IEEE, ACM, 4(2),

pp.163–75. Available at: http://www.ncbi.nlm.nih.gov/pub-

med/17473311.

Xiao, X. et al., 2003. Gene clustering using self-organizing

maps and particle swarm optimization. Parallel and Distributed

Processing Symposium, 2003. Proceedings. International, 0(C),

p.10–pp. Available at: http://ieeexplore.ieee.org/xpls/abs_all.

jsp?arnumber=1213290.

Yang Lou, Junli Li, and Y.W., A Binary-Differential Evolution

algorithm based on Ordering of individuals. IEEE Natural Com-

putation (ICNC), 2010 Sixth International Conference on.

Yeung, K.Y. & Ruzzo, W.L., 2001. Principal component analy-

sis for clustering gene expression data. Bioinformatics, 17(9),

pp.763–774. Available at: http://www.cs.washington.

Yu, X., Yu, G. & Wang, J., 2017. Clustering cancer gene expres-

sion data by projective clustering ensemble. Plos One, 12(2),

p.e0171429. Available at: http://dx.plos.org/10.1371/journal.

pone.0171429.

Yu, Z. et al., 2013. for Tumor Clustering from Biomolecular

Data. , 10(3), pp.657–670.

Zaït, M. & Messatfa, H., 1997. A comparative study of cluster-

ing methods. Future Generation Computer Systems - Special

double issue on data mining, Volume 13(Issue 2-3), p.Pages

149-159.

Zou, D. et al., 2013. A modi ed differential evolution algo-

rithm for unconstrained optimization problems. Neurocomput-

ing, 120, pp.469–481.