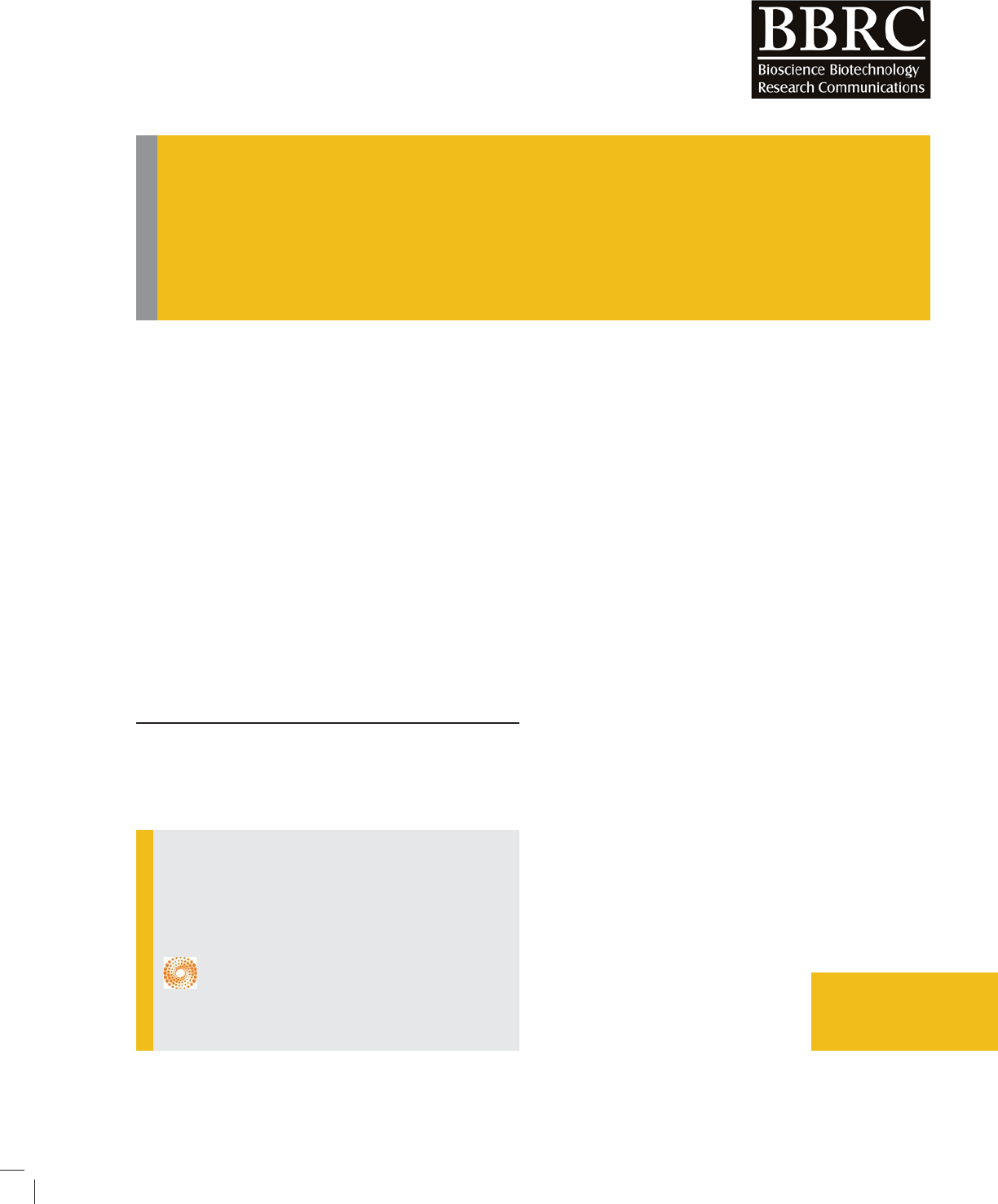
Biotechnological

Communication

Biosci. Biotech. Res. Comm. 9(4): 625-632 (2016)

Biokinetic modeling for aerobic treatment of aqueous

phase of oil-water emulsion

Alireza Nazari Alavi

*, Mohammad Mirzai

, Ali Akbar Sajadi

and Hamed Hasanian

Institute of Water and Energy, Sharif University of Technology, P.O. Box 11155-8639, Tehran, I.R. Iran

Faculty of Environment, University of Tehran, P.O. Box 14155-6135, Tehran, I.R. Iran

ABSTRACT

Discharge of used cutting oil (oil-water emulsion) to the environment is not allowed without proper treatment.

Usually, more than 90% of oil-water emulsion used in machine shop wastes is water. After separation of oil from

water, further treatment of aqueous phase could be carried out by biological methods. In this paper, an experimental

method is developed in a batch reactor. The ratio of initial substrate to the initial biomass concentration is adjusted to

be between 0.9< S0/X0 <10. Biomass concentration, COD, nutrient (nitrogen & phosphor) and suspended solid were

determined for different ratio of S0/X0. The achieved data were applied to determination of kinetic model parameters.

These parameters can be used in designing treatment plants of oil-water emulsions. In this paper, mathematical model

based on live biomass is used for simulation of experimental data from biological treatment of oil-water emulsion in

aqueous phase. Newton numerical method is selected for determination of model’s parameters. Results show adjust-

ment of presented model with experimental data. According to the results, constant parameters of speci c growth

rate and conversion rate of substrate to biomass are determined. Achieved results are in a good accordance with the

Monod model and it strongly supports that aqueous phase of oil-water emulsion has a suitable capability of biologi-

cal treatment.

KEY WORDS: BIOLOGICAL TREATMENT; OIL-WATER EMULSION; AQUEOUS PHASE; MODELING

625

ARTICLE INFORMATION:

*Corresponding Author: alavi@sharif.edu

Received 1

Nov, 2016

Accepted after revision 25

Dec, 2016

BBRC Print ISSN: 0974-6455

Online ISSN: 2321-4007

Thomson Reuters ISI ESC and Crossref Indexed Journal

NAAS Journal Score 2015: 3.48 Cosmos IF : 4.006

reserved.

Online Contents Available at: http//www.bbrc.in/

INTRODUCTION

Water is used in almost all industries and is converted

to waste water. Usually it should be treated to the stand-

ard level before discharging to the environment or reus-

ing. Emulsion system is generated in widespread type

of industries such as cosmetics, pharmaceutics, biologi-

cal systems, petroleum plants, food industries. Cutting

oil waste water is generated in machine shop wastes

consists of an emulsion of oil and water (O/W). Main

626 TREATMENT OF OIL-WATER EMULSION BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Alireza Nazari Alavi et al.

functions of this cutting oil are lubrication, friction

reduction and cooling of mechanical parts. This waste

water is classi ed as a toxic waste due to existence of

some additive material used for corrosion prevention as

well as bacterial growth. Treatment of this waste water

is a special problem for industries located inside cit-

ies and towns. Importance of treatment of such oil and

wastewater increases due to sewage collection network

de ciencies especially in developing countries, (Arif n

et al 2016).

Rheological behavior investigation of O/W emulsions

has been carried and it was found that viscosities of

emulsion and also the stability of emulsions are strongly

affected by shear rate, temperature, water contents,

interfacial tensions and particles nature O/W emulsions

are thermodynamically unstable and breaking down the

emulsion (separation of water and oil) which normally

consist 1-10% oil and the rest water, enables the biologi-

cal treatment of aqueous phase. The biological treatment

of aqueous phase in machine shop wastes could be car-

ried out similar to the procedure reported for treatment

of agro-industries wastes, such as ef uent from olive

mills which constitutes a serious environmental prob-

lem especially in the Mediterranean Sea region (Mant-

zavinos & Kalogerakis 2005, Berton-Carabin et al. 2014,

Ahmadi-Dastgerdi et al. 2015, and Arif n et al. 2016).

Importance of cutting oil wastewater treatment is

reported in many recent studies. Prediction the rate of

pollutants removal from aqueous solutions is neces-

sary in order to design a treatment plant (Souza et al.

2016). Biodegradability of oil-water emulsion is under

the question due to high pollution (COD=60g/l) and also

presence of undesirable material such as antibacterial

material in the emulsion and it has led the research-

ers to use physicochemical processes such as membrane

separation (reverse osmosis\ultra  ltration) (Portela et al.

2001, Hadj et al. 2004), electro coagulation hydrother-

mal oxidation (Deepak et al., 1994, Sanchez et al. 2007)

and using nanoparticles. Other researchers have also

reported biological treatment application for solving this

environmental concern (Krstic et al., 2007, Hesampour

et al. 2008, Kobya et al. 2008, Rios et al. 1998, Rella et

al. 2003, Bensadok et al. 2007, Abdel-Aziz et al. 2016),

Kalliola et al. 2016).

Biodegradability of wastewater in a batch reactor

were evaluated to show its ef ciency, i.e., for investi-

gation of biodegradable material such as nitrate (Kris-

tensen et al. 1992), soluble organic carbon (Servais et al.

1987) and bacterial counting (Munch & Pollard 1997).

Quality and progress rate in a batch reactor is con-

trolled by ratio of initial substrate (S

) according to COD

or BOD to initial biomass concentration (X

) according

to MLVSS or MLSS (Chudoba et al., 1992, Spanjers &

Vanrolleghem 1995, Kappeler & Gujer 2005).

Low quantity of S

usually makes microorganism’s

growth investigation impossible, on the other hand at

higher quantities of (S

>1) microorganism’s growth

will be measurable and it can be used in explanation

of experimental results and modeling of reaction rate

(Wentzel et al. 1995).Veri cation of biological treat-

ment in this region develops results to the conventional

systems similar to SBR with so many advantages have

reported about its function (Irvine et al. 1983). One of

the major advantages of SBR systems is the ability to

treat wastewaters with varying organic loadings with

different ratios of S

(Jamrah & Abu-Ghunmi 2005).

Since having a sedimentation tank is not required in this

process, therefore, it is suitable for use in small scale

industries located inside of towns.

Concentrations of substrate in in uent and in out-

 ow as well as retention time are important keys in per-

formance of activated sludge process. These data often

are suf cient to produce simple models like Monod.

However for models with complicated concepts, it is

necessary to study more about other factors like as inhi-

bition effect. It is known that Inhibition can affect mass

transfer and concentration of substance during start up

time which affects microorganism growth. Therefore it

is obvious that accommodation of experimental data

with the complicated models and determination of their

parameters is a dif cult process. Due to the fact that

mathematical models are complex and it is too hard to

solve them with analytical methods, researchers prefer

to solve them by advanced regulated and numerical

methods. As a matter of fact, application of numerical

method is a procedure to solve occurred problems during

the process of experimental data.

Mathematical models such as the Monod kinetic

model,  rst-order substrate removal model, Grau sec-

ond-order model, and Stover-Kincannon model have

been used to design speci c unit operations, optimize

and control treatment processes, understand the under-

lying biotechnology, and transport mechanisms within

the reactor (Fu et al. 2013). Monod model is based on the

results of batch reactor system for pure culture which fed

by simple nutrient. While the Monod model has some

success in describing steady state growth rates, it has

been found to be inadequate to predict where the ini-

tial data does not correspond to the globally attracting

steady state (Meng et al. 2010). Effect of concentration

of contaminant in in uent of a reactor on concentra-

tion of that contaminant in output of reactor, variation

of semi saturation constant (K

) and effect of inhibi-

tive substance in medium are reported de ciencies of

this model (Orhon & Tunay 1979). Constant logarith-

mic growth rate is basic thesis of this model whereas

this concept is a challenging subject. Researchers have

proved that there is not a speci c constant growth rate

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS TREATMENT OF OIL-WATER EMULSION 627

Alireza Nazari Alavi et al.

for mixed bulk of bacteria (Grady & Williams 1975).

There is a straight relation between constant growth rate

and initial concentration of contaminant. If the concen-

tration of contaminant increases, the constant of growth

rate will decrease. It means contaminant with high con-

centration operates as an inhibitor.

Variation trend of X/X

to S/S

should be increasing

otherwise it is probable that there is an inhibitor fac-

tor in the environment which affects on the microor-

ganism’s growth and activity. Research have presented

that aforementioned trend inclines to an asymptote, it

reveals that there is a factor that affect the live biomass

production. Goal of this study is to investigate biologi-

cal treatment of liquid phase of oil-water emulsion in a

batch reactor and to presents a model which consists of

effective factors by numerical methods

MATERIAL AND METHODS

EXPERIMENTAL SETUP

Cutting oil from a local supplier was used in this study.

Oil-water emulsions were made arti cially in this labora-

tory and then it was broken by adding Calcium Chloride

to separate two phases and obtain the aqueous phase.

Sewage (oil-water) consists of 2% oil and 98% water. To

ful ll this task, 1 g of CaCl

was added to emulsion for

each percent of oil and after complete mixing it was left

for one day in decanter ampoule to separate the aque-

ous phase.

Gradual increasing of oily water concentration was

used to study compatibility of activated sludge with sew-

age. For this purpose 3 lit sludge (MLSS=1.8g/l) mixed

with 3 lit sewage (30% oily water plus 70% water) and

aerated for one day. After aeration period and 2 hours

for settlement, 3 lit of reactor replaced by sewage with

40% oily water. This process continued up to reaching

sewage with 100% oily water. This compatible and aer-

ated sludge was used in experiments. Schematic drawing

of experimental set up is shown in Figure 1.

All experiments were performed in ambient tempera-

ture at about 21˚C. The pH for aqueous phase was neu-

tral and almost constant (6.9-7) therefore, it didn’t need

further adjustment. Dissolved oxygen during the experi-

ment was measured between 6.5-7.2mg/l. Required

parameters such as COD, nutrient (nitrogen & phosphor)

and suspended solid were measured according to the

Standard Methods and were controlled before each test

(APHA 1999). During the experiment, ratios of initial

substrate concentration to initial biomass concentration

were 0.9, 1.3, 2.2, 5.86, 10 and samplings were done by

an ampoule at the one third heights from the surface.

NEWTON’S METHOD TO SOLVE EQUATION

Newton iterative numerical method is used to determine

parameters of presented model. In Newton method, for

a continues and differentiable function on the interval

(a,b), function f is approximated by its tangent line in an

arbitrary initial value x0, initial guess could be reason-

ably close to the true root to better convergence.

By computing x-interception of tangent line, a better

approximation to the function’s root obtained in each

step and iteration can be continued to reaching a rea-

sonable approximation of root as X

n+1

(1)

DEVELOPING MONOD MODEL

Explanation of some basic concept is necessary before

presentation of the model which based on the obtained

experimental data. The most current available model is

the Monod model which stated in equations 2 and 3

(Tchobanoglous & Burton 1991):

(2)

(3)

µ: speci c growth rate (time inverse)

max

: maximum speci c growth rate (time inverse)

FIGURE 1. Experimental setup.

628 TREATMENT OF OIL-WATER EMULSION BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Alireza Nazari Alavi et al.

: semi saturation constant (mg/l )

X: biomass concentration (mg/l )

S: substrate concentration (mg/l )

Concentration of biomass in reactor is usually meas-

ured by MLSS. This parameter comprises all live, just

active, microorganisms and remained cells; therefore it

is not a representative parameter for reactions (Weddle

& Jenkins 1971). Thus researchers tried to give a more

precise de nition of existence biomass as follows:

(4)

Where X

is biomass concentration which can repro-

duce, X

is just active biomass (organic oxidation),

is dead or inactive biomass and P is remained cells

and biopolymers. X

and X

can be realized by painting

method (Jones 1987). Measurement of X

is so dif cult

and its quantity is not considerable and usually consid-

ered negligible or may be merged by X

. If P in compari-

son with X

is small, live biomass growth rate can

be de ned as:

(5)

Biomass variation rate in a reactor depends on the repro-

duction rate (r

) and death rate (r

) as follow:

(6)

From a practical point of view, determination of biomass

growth rate is very dif cult; therefore a relationship is

described between MLSS and live biomass. For this pur-

pose primary live biomass rate is de ned as:

(7)

According to classic law of cell reproduction, real rate

of live biomass growth can be considered zero-order to

substrate and  rst-order to X

(8)

On the other point of view, velocity of losing produc-

tion power depends on cell concentration and inhibitor

substance as follow:

(9)

Where  is kinetic coef cient of missing reproducibil-

ity and I is concentration of produced inhibitor sub-

stances which are produced by microbial production as

follow:

(10)

Therefore equation 6 is rewritten as follow:

(11)

At the steady state and live biomass concentration

) is the maximum, therefore:

(12)

By replacing in equation 11, live biomass growth rate

can be written as:

(13)

This equation has been used by most of researchers

for evaluation of biomass consensus rate (Tulear &

Eharaclis 1982, Vavilin & Vsiliev 1983).

By de ning

max maxvo

XXX

and

XXX

, equa-

tion 13 is rewritten as:

(14)

By integration from equation 14, real concentration of

biomass during the time is obtained as:

(15)

By using this equation and experimental results,

parameters 

and K

can be calculated by adjusting

numerical methods and veri ed by substrate removal

rate model. To achieve this goal, mathematical equa-

tion for substrate removal model should be determined.

Conversion rate (Y

obs

) is de ned by observed substrate

removal rate and biomass growth rate as follows (sub-

strate removal rate usually is measured by COD or BOD).

(16)

(17)

obs

remains constant during the experiments and is

equal to:

(18)

By replacing in equation 14 and integration, function of

substrate removal during the time can be determined as:

(19)

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS TREATMENT OF OIL-WATER EMULSION 629

Alireza Nazari Alavi et al.

Where is the indicator of primary amount of

substrate which can produce primary live biomass (X

)

by digestion. Applying Newton method as a numerical

method to equation 15 and 19 facilitates  nding kinetic

parameters of reaction such as biomass growth rate and

substrate removal rate.

RESULTS AND DISCUSSION

EXPERIMENTAL RESULTS

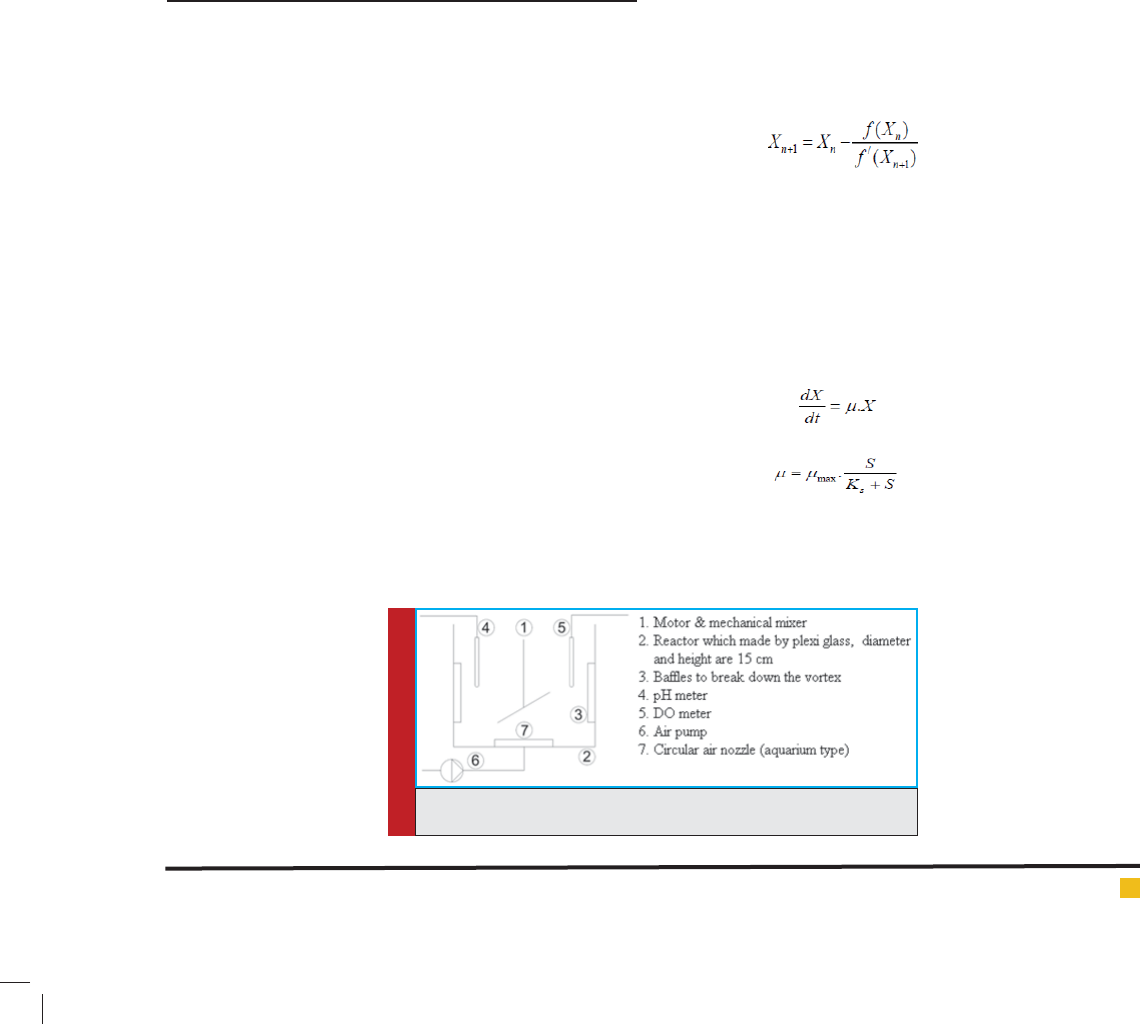
As it was stated before, ratios of during experiments

were 0.9, 1.3, 2.2, 5.86 and 10. For instance, variation of

biomass concentration (MLSS) and substrate concentra-

tion (COD) versus time for =1.3 which are the basis of

kinetic modeling of reaction are shown in Figure 2.

VERIFYING MONOD MODEL WITH

EXPERIMENTAL RESULTS

Conversion rate of substrate to biomass usually is used

to solve differential equation of Monod equation accord-

ing to variable X. This equation is simpli ed as follow in

exponential growth phase:

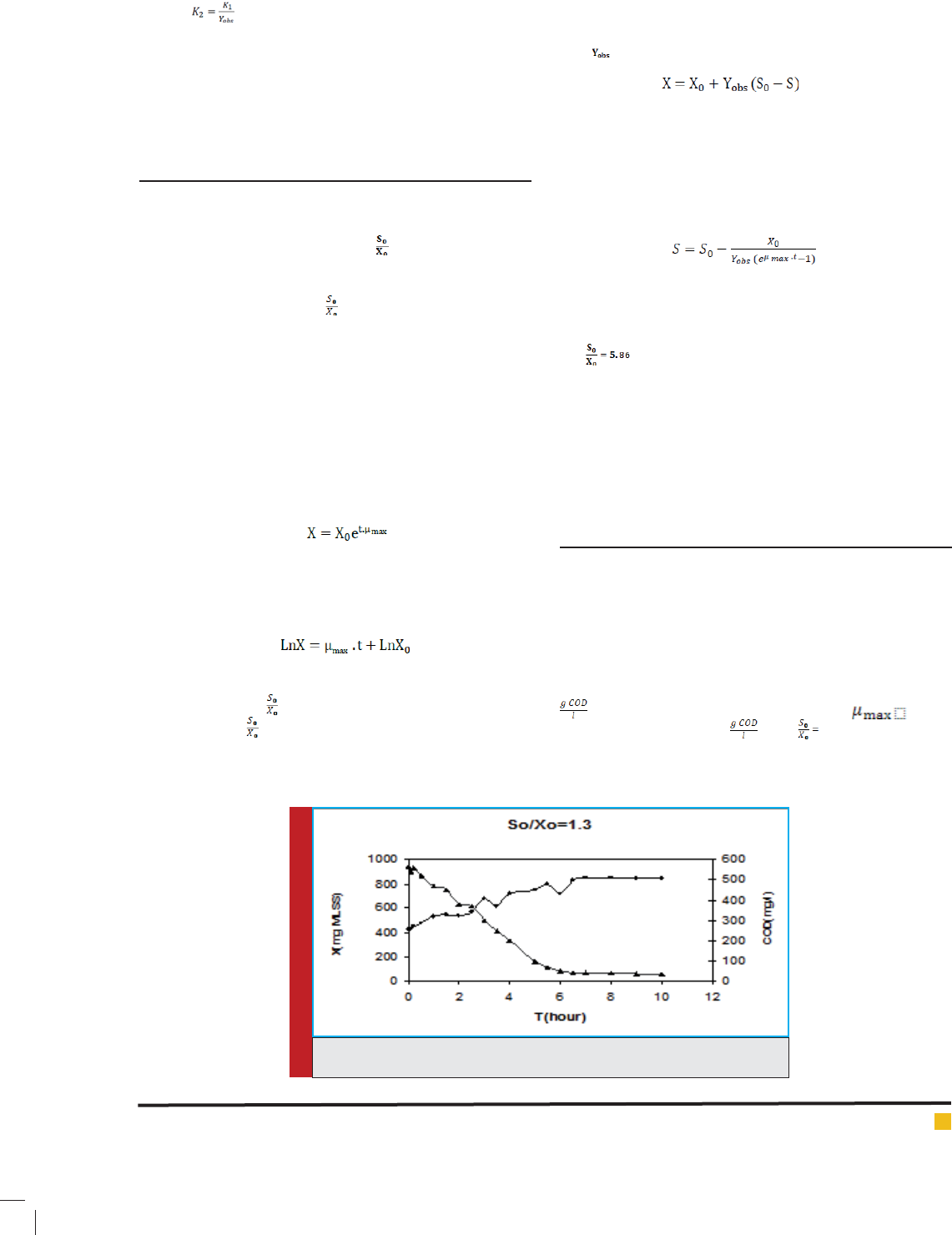
(20)

If is determined, calculating the biomass concentration

during the time by equation 21 will be possible

can be

determined as gradient of following equation:

(21)

Figure 3 shows aforementioned function in exponential

growth phase for

= 5.86 and Table 1 lists µ

max

for dif-

ferent value of .

Calculation was based on presumption that conver-

sion rate of substrate to biomass (Y

obs

) during the experi-

ment is constant, con rming this presumption is neces-

sary. Y

obs

can be calculated from equation 22. Table 1

lists for different value of

Parameters of model must be veri ed, so parameters

resulted from experiments must be usable in model for

calculating other variables in order to accept the model.

Equation 23 is used in exponential growth phase in

Monod model for forecasting substrate concentration

during the time.

Comparison between calculated and measured substrate

during the time is necessary for veri cation of model

and experimental results. This comparison presented

for = 5.86 in Table 2. Differences in exponential

growth phase are about 5.8%.

Certainty of Monod model is under discussion from

the past as it was stated in introduction. Main idea of

Monod model is based on that exponential speci c

growth rate (µ) remains constant. In the present experi-

ments µ

can be considered near constant.

DISCUSSION ABOUT THE PRESENTED MODEL

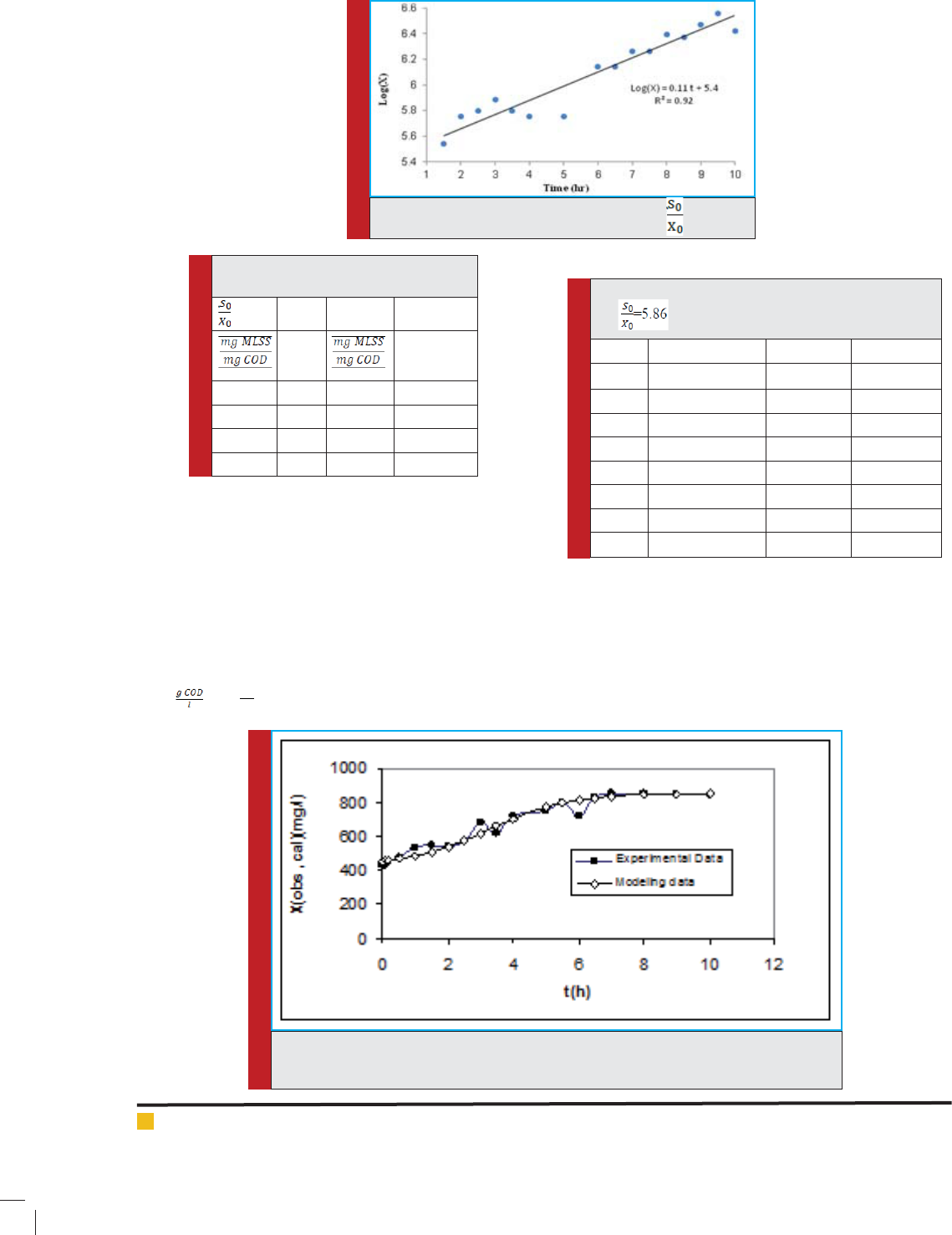
Analysis of biomass growth rate according to pre-

sented model should be discussed. Figure 4 illustrates

both experimental data and results which derived from

numerical analysis of presented model.

As it is shown, the presented model is well compatible

with experimental data. Numerical analysis outcome is

optimum value for kinetic parameters namely K

=27

and h

-1

. Sanchez (2007) determined equal

to 0.01 h

-1

and K

= 16 for =1 for an ef uent

derived from the anaerobic digestion of two-phase olive

mill solid residue (Sanchez et al. 2007). Bajaj (2009)

FIGURE 2. Biomass and substrate variation during time for .

(22)

(23)

Alireza Nazari Alavi et al.

630 TREATMENT OF OIL-WATER EMULSION BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

FIGURE 3. Biomass variation versus time for = 5.86.

Table 1: Y

obs

and removal ef ciency

for different values of S

max

obs

Difference

-1

0.9 0.099 0.61 90

2.2 0.12 0.83 83

5.86 0.11 0.39 85

10 0.14 0.41 90

Table 2: Calculated and measured S during the time

for

Time S (Experiment) S (model) Difference

Hr mg/lit mg/lit %

2 1256 1304 4

4 1067 1224 13

5 956 1080 11

6 832 968 14

7 694 732 5

8 539 580 7

10 174 320 46

FIGURE 4. Comparison between experimental data and results from presented model for

biomass growth.

determined 

max

=0.3095 h

-1

for biodegradation of phenol

with a mixed bacterial consortium in batch conditions

(Bajaj et al. 2009).

If the parameters of biomass growth rate which derived

from presented model are correct, they should be veri ed

in the substrate removal modeling. Therefore according

to equation 18, Y

obs

(tangent of function S=f(X)) should

remain constant; Figure 5 shows this function.

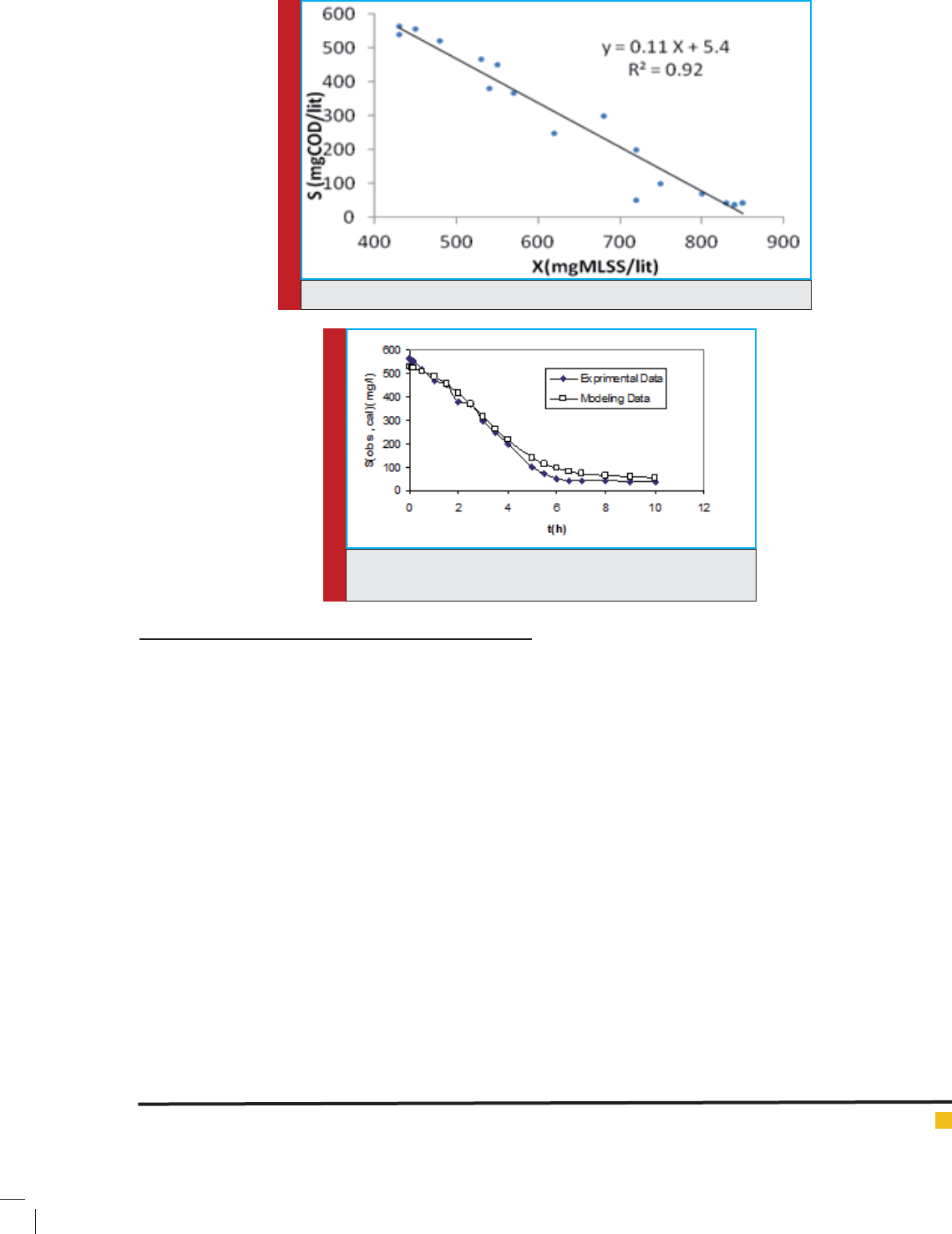
As it is indicated above, Y

obs

is equal to 0.728 and as it

is supposed to be constant, K

can be calculated as equal

to 37

for



1.3.

Afterward, substrate removal can be calculated by

equation 22 during the time and can be compared with

experimental data.

As it is indicated in Figure 6, experimental results are

in accordance with calculated parameters for substrate

concentration. It follows that model and is completely

veri ed with experimental results.

Alireza Nazari Alavi et al.

BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS TREATMENT OF OIL-WATER EMULSION 631

CONCLUSION

The research shows that aqueous phase of oil-water

emulsion has a suitable capability of biological treat-

ment. Kinetic parameters of biological treatment, which

are the basis of modeling, are determined. These param-

eters can be utilized to increase the ef ciency of design-

ing units of treatment plants of O/W emulsions. Compat-

ibility of the process with the Monod model shows that

this model is an acceptable descriptor for O/W emul-

sion and can be used in designing process.In the future

studies about biological treatment of aqueous phase of

oil-water emulsion, to increase the accuracy and com-

patibility of the model, kinetic of live biomass which are

able to reproduce should be considered with real growth

rate of . Also it should be noticed that dead biomass acts

as an inhibiting factor.

REFERENCES

Abdel-Aziz, M. H., El-Ashtoukhy, E. S., Zoromba, M. Sh. and

M. Bassyouni (2016). Oil-in-water Emulsion Breaking by Elec-

trocoagulation in a Modi ed Electrochemical Cell. Interna-

tional Journal of Electrochemical Science, 11, pp. 9634-9643

Ahmadi-Dastgerdi, A., Nasirpour, A., Rahimi, E. (2015). Phys-

ical and Rheological Properties of Oil in Water Heat Stable

Emulsions Made from Different Stabilizers. Journal of Food

Biosciences and Technology,5(1), pp. 45-62

APHA (1999). Standard Methods for the examination of water

and wastewater. 20th Edn.

Arif n, Tajnor S. T., Yahya, Effah and Husin, Hazlina (2016).

The Rheology of Light Crude Oil and Water-In-Oil-Emulsion.

Procedia Engineering, 148, pp. 1149-1155

Bajaj, M., Gallert, C and Winter, J.(2009). Phenol degrada-

tion kinetics of an aerobic mixed culture. Bioch. Eng. J.2(46),

pp. 205-209

Bensadok, K., Belkacem, M. & Nezzal, G. (2007). Treat-

ment of cutting oil/water emulsion by coupling coagulation

and dissolved air  otation. Desalination, 206(1), pp. 440-

448

Berton-Carabin, Claire C. C., Ropers, Marie Helene & Genot,

Claude (2014). Lipid Oxidation in Oil-in-Water Emulsions:

Involvement of the Interfacial Layer. Comprehensive Reviews

in Food Science and Food Safety 13, pp. 945-977

Chudoba, P., Capdeville B. and Chudoba J. (1992).Explanation

of biological meaning of the S0/X0 ratio in batch cultivation.

Wat. Sci. and Tech., 26(3-4), pp. 743-751

FIGURE 5. Substrate concentration versus biomass growth for S

= 5.86.

FIGURE 6. Comparison between experimental data and results

from presented model for substrate removal.

Alireza Nazari Alavi et al.

632 TREATMENT OF OIL-WATER EMULSION BIOSCIENCE BIOTECHNOLOGY RESEARCH COMMUNICATIONS

Deepak, D., Anand, V. and Bhargava, R. (1994). Biodegradation

kinetics of metal cutting oil: evaluation of kinetic parameters.

The Chem. Eng. J.,56, pp. 91-96

Fu, X., Zhenxing, H. and Hengfeng, M. (2013) Identical full-

scale biogas-lift reactors (BLRs) with anaerobic granular

sludge and residual activated sludge for brewery wastewater

treatment and kinetic modeling, J. of Env. Sci. 25(10), pp.

2031-2040

Grady, P. and Williams, D. (1975) Effects of in uent substrate

concentration on the kinetics of naturel microbial population

in continuous culture, Wat. Res., 9 (2), pp. 171-180

Hadj, Z., Amel, Z. and Moulay, S. (2004). Microemulsion

breakdown using the pervaporation technique:application to

cutting oil models, Desalination, 170(1), pp. 91-97.

Hesampour, M., Krzyzaniak, A. and Marianne, N. (2008). The

in uence of different factors on the stability and ultra ltration of

emulsi ed oil in water, J. of Membrane Sci., 325(1), pp. 199–208

Irvine, L., Ketchum, H., Breyfogle, R. and Barth, F. (1983).

Municipal application of sequencing batch treatment, J. of

WPCF. 55(5), pp. 484-493

Jamrah, A. and

Abu-Ghunmi, L. (2005). One independent

variable rate equation describing utilization of biodegradable

organic matter in activated sludge processes. Env. Mod. and

Ass., 10, pp. 21–31.

Jones, P. (1987). Measures of Yeast Death and Deactivation

and Theire Meaning , Pro. Bioch.22(4), pp. 118-128

Kalliola, Simo, Repo, Eveliina, Sillanpää, Mika, Arora Jaspreet

Singh, He, Jibao & John T. Vijay (2016). The stability of green

nanoparticles in increased pH and salinity forapplications in

oil spill-treatment. Colloids and Surfaces A: Physicochemical

and Engineering Aspects, 493, pp. 99-107.

Kappeler, J. and Gujer, W. (2005). Estimation of kinetic

parameters of heterotrophic biomass under aerobic condition

and characterization of wastewater for activated sludge mod-

elling. Wat. Sci. and Tech., 25(6), pp. 125-139

Kobya, M., Ciftci, C., Bayramoglu, M. and Sensoy, T. (2008)

Study on the treatment of waste metal cutting  uids using

electrocoagulation, Sepa. and Pur. Tech., 60(3), pp. 285–291

Kristensen, H., Jourgensen, E. & Henze, M. (1992). Charac-

terization of functional microorganism groups and substrate in

activated sludge and wastewater by AUR, NUR and OUR. Wat.

Sci. and Tech,. 25(6), pp. 43-57(1992).

Krstic, M., Ho inger, W., Koris, K. and Vatai, G. N. (2007).

Energy-saving potential of cross- ow ultra ltration with

inserted static mixer: Application to an oil-in-water emulsion,

Sepa. and Pur. Tech., 57(1), pp. 134–139

Mantzavinos, D. and Kalogerakis, N. (2005).Treatment of olive

mill ef uents: Part I. Organic matter degradation by chemical

and biological processes, An overview. Env. Int., 2 (31), pp.

289- 295

Meng, X.,

Gao, Q. and Li, Z. (2010). The effects of delayed

growth response on the dynamic behaviors of the Monod type

chemostat modelwith impulsive input nutrient concentration,

Nonlinear Analysis: Real World App., 11(5), pp. 4476-4486

Munch, E. and Pollard, C. (1997).Measuring bacterial biomass-

COD in wastewater containing particular matter.

Wat. Res., 10( 31), pp. 2252-2256

Orhon, D. andTunay, O. (1979). Mathematical models of bio-

logical waste treatment processes for the design of aeration

tanks discussion. Wat. Res., 13(6), pp. 127-135

Portela, J. R., Lopez, J., Nebot, E. & Maertinez, O. (2001). Elimi-

nation of cutting oil wastes by promoted hydrothermal

oxidation, J.of Hazardous Mat., 88(1), pp. 95–106

Rella, R., Sturaro, A., Parvoli, G., Ferrara, D. and Doretti, L.

(2003). An unusual and persistent contamination of drinking

water by cutting oil, Wat. Res., 37(3), pp. 656–660

Rios, G., Pazos, C. and Coca, J. (1998). Destabilizationof cut-

ting oil emulsions using inorganic salts as coagulants, Colloids

and Surfaces, A: Physicochemical and Eng. Aspects.Colloids

and Surface 138(2-3), pp. 383–389

Sanchez, E.

, Rincón, B., Borja, R., Travieso, L. and Raposo,

(2007).Aerobic degradation kinetic of the ef uent derived

from the anaerobic digestion of two-phase olive mill solid resi-

due, Int. Biodet. and Biodeg. 60(1), pp. 60-67

Sanchez, E., Rincón, B., Borja, R., Travieso, L. and Raposo, F.

(2007). Hydrothermal oxidation: Application to the treatment

of different cutting  uid wastes, J. of Hazardous Mat., 144(3)

pp. 639-644

Servais, P., Gilles, G. and Hascoët, M. (1987).Determination of

biodegradable fraction of dissolved organic matter in waters,

Wat. Res. 21(4), pp. 445-450

Souza, R. S., Porto, P. S., Pintor, A. M., Ruphuy, G., Costa, M.,

Boaventura, R. A. and Vilar, V. J. (2016). New insights on the

removal of mineral oil from oil-in-water emulsions using cork

by-products: Effect of salt and surfactants content, Chemical

Engineering Journal, 285, pp.709–717

Spanjers, H. and Vanrolleghem, P. (1995). Respirometry as a

tool for rapid characterizaton of wastewater and activated

sludge, Wat Sci. and Tech., 31(2), pp. 105-114

Srinivasan, A. and Viraraghavan, T. (2010).Oil removal from

water using biomaterials, Bioresource Tech., 101(17),pp. 6594–

6600

Tchobanoglous, G. and Burton, Franklin L.

(1991). Wastewater

Engineering Treatment, Disposal and Reuse, McGraw-Hill Inc.,

4th Edn.

Tulear, M. and Eharaclis, W. (1982).Dynamics of Bio lm Pro-

cesses, Journal of Water Pollution Control Federation, 9(54),

pp. 1288-300

Vavilin, V. and Vsiliev V. (1983). Dependance of biological

treatment rate an species composition in activated sluge or

bio lm, Biotech. Bioeng.25(6), pp. 1521-1538

Weddle, C. and Jenkins, D. (1971).The viability activity of acti-

vated sluge, Wat. Res. 5, pp. 621-628

Wentzel, C., Mbewe, A., Lakay, T. and Ekama, G.A. (1995).Batch

test for measurement of readily biodegradable COD and active

organism concentration in municipal watewater, Water S.A,

21(2), pp. 117-124